ＤＸライブラリとブレゼンハムのアルゴリズムを使って線分を描画

ブレゼンハムのアルゴリズムは、線分をドットの集まりで近似するためのアルゴリズムであり、計算機にとって比較的重い処理である乗算や除算を用いずに実装することが可能である。

実装例

以下にC++のコードを示す。このコードにはＤＸライブラリが用いられており、GCC 4.8.1およびＤＸライブラリ Ver3.16で動作確認を行った。

線分の両端の丸をマウスでドラッグすることにより、始点や終点の位置を移動できる。
また、テンキーではない方の1, 2, 3キーを押すことで、描画アルゴリズムを切り替えることができる。

senbun_byouga.cpp

#include <DxLib.h>

// 標準関数で線分を描画する
void drawline(int sx, int sy, int dx, int dy) {
	DrawLine(sx, sy, dx, dy, GetColor(255, 128, 128));
}

// プレゼンハムのアルゴリズムっぽい感じで線分を描画する
void bresenham(int sx, int sy, int dx, int dy) {
	int color = GetColor(128, 255, 128);
	int x = sx, y = sy; // 現在位置
	int wx = (sx >= dx ? sx - dx : dx - sx); // x座標の差の絶対値
	int wy = (sy >= dy ? sy - dy : dy - sy); // y座標の差の絶対値
	int xmode = (wx >= wy); // x方向の変位がy方向の変位以上か
	int gosa = 0;
	while (x != dx || y != dy) {
		DrawPixel(x, y, color); // とりあえず 現在位置に 点を打つ (川柳)
		if (xmode) { // x方向の変位の方が小さくないので、主にx方向に移動する
			if (sx < dx) x++; else x--; // x方向に進む
			// y方向に進むべき変位を進んでいないので、誤差として加える
			// 誤差は整数にするために(wx * 2)倍で扱う
			gosa += ((dy - sy) << 1);
			if (gosa > wx) { // yの正の方向に進むべきなのに進んでいない誤差が0.5を超えた
				y++; // yの正の方向に進む
				gosa -= (wx << 1); // 進んだ分を誤差に反映させる
			} else if (gosa < -wx) { // yの負の方向(ry
				y--; // yの負(ry
				gosa += (wx << 1); // 進んだ(ry
			}
		} else { // y方向の変位の方が大きいので、主にy方向に移動する
			// xの時と同様
			if (sy < dy) y++; else y--;
			gosa += ((dx - sx) << 1);
			if (gosa > wy) {
				x++;
				gosa -= (wy << 1);
			} else if (gosa < -wy) {
				x--;
				gosa += (wy << 1);
			}
		}
	}
}

// 8方向のうち一番終点に近づく方向に移動する(失敗)
void donyoku(int sx, int sy, int dx, int dy) {
	int color = GetColor(128, 128, 255);
	int x = sx, y = sy;
	while (x != dx || y != dy) {
		DrawPixel(x, y, color);
		int nx = sx, ny = sy, score = -1;
		for (int deltay = -1; deltay <= 1; deltay++) {
			for (int deltax = -1; deltax <= 1; deltax++) {
				int cx = x + deltax, cy = y + deltay;
				int cscore = (dx - cx) * (dx - cx) + (dy - cy) * (dy - cy);
				if (score < 0 || cscore < score) {
					score = cscore;
					nx = cx;
					ny = cy;
				}
			}
		}
		x = nx;
		y = ny;
	}
}

int WINAPI WinMain(HINSTANCE, HINSTANCE, LPSTR, int) {
	if (ChangeWindowMode(TRUE) != DX_CHANGESCREEN_OK || DxLib_Init() != 0) return -1;
	SetDrawScreen(DX_SCREEN_BACK);

	void (*func[3])(int, int, int, int) = {
		drawline, bresenham, donyoku
	};
	const char *name[3] = {"DrawLine", "プレゼンハム", "貪欲"};
	int method = 0;

	int msx = 0, msy = 0, mox = 0, moy = 0, mflag = 0;

	int sx = 100, sy = 100, dx = 400, dy = 300;

	while (ProcessMessage() == 0 && ClearDrawScreen() == 0) {
		char key[256];
		int mx, my;
		GetHitKeyStateAll(key);
		GetMousePoint(&mx, &my);
		if (key[KEY_INPUT_1]) method = 0;
		if (key[KEY_INPUT_2]) method = 1;
		if (key[KEY_INPUT_3]) method = 2;

		if (GetMouseInput() & MOUSE_INPUT_LEFT) {
			if (mflag == 0) {
				msx = mx;
				msy = my;
				if ((mx - sx) * (mx - sx) + (my - sy) * (my - sy) <= 9) {
					mox = sx;
					moy = sy;
					mflag = 1;
				} else if ((mx - dx) * (mx - dx) + (my - dy) * (my - dy) <= 9) {
					mox = dx;
					moy = dy;
					mflag = 2;
				} else {
					mflag = 3;
				}
			}
			if (mflag == 1) {
				sx = mox + mx - msx;
				sy = moy + my - msy;
			} else if (mflag == 2) {
				dx = mox + mx - msx;
				dy = moy + my - msy;
			}
		} else {
			mflag = 0;
		}

		DrawString(10, 10, name[method], GetColor(255, 255, 255));
		DrawCircle(sx, sy, 3, GetColor(255, 255, 255), FALSE);
		DrawCircle(dx, dy, 3, GetColor(255, 255, 255), FALSE);
		func[method](sx, sy, dx, dy);

		ScreenFlip();
	}

	DxLib_End();
	return 0;
}

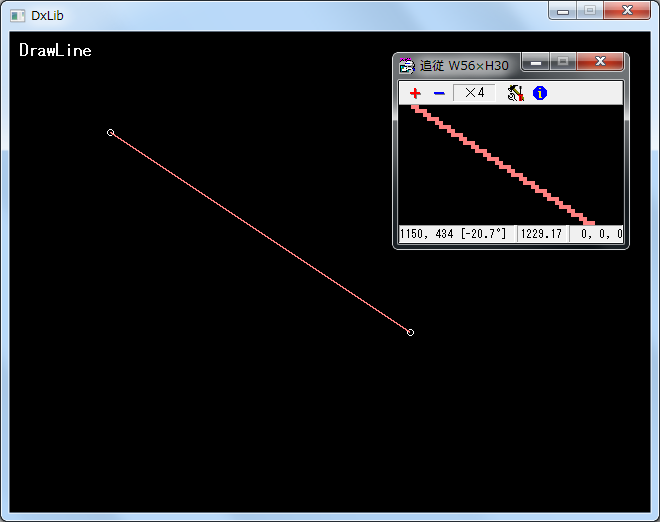
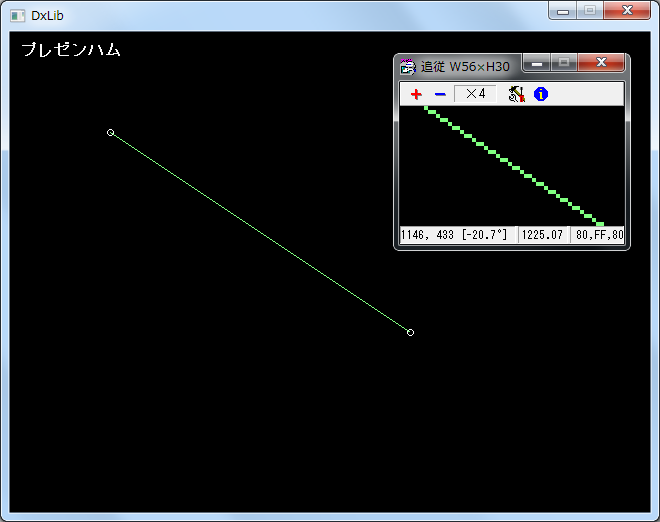
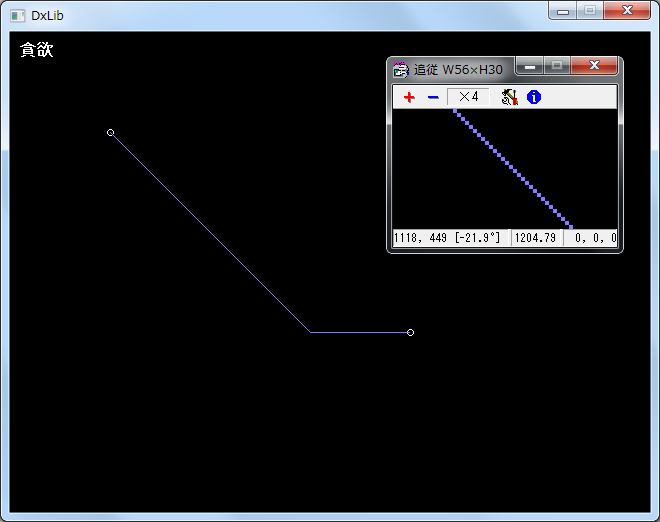
実行結果

各アルゴリズムでの描画結果に、デスクトップの拡大鏡 MeGaZoomで描画された線の一部を拡大した画像を合成した。

(この環境の?) 標準DrawLineでは、拡大すると線にかぶりがあり、太めに描画されていることがわかる。
また、この貪欲ではななめ45度に行ってしまい、1本の線分で結ぶことはできなかった。