問題
$1$ から $N$ の番号がついた $N$ 頂点の木 ($1 \leq N \leq 10^5$) が与えられ、それぞれの頂点に正の整数 $C_i$ ($1 \leq i \leq N$) が割り当てられている。
この木における頂点 $a$ と頂点 $b$ の間にある辺の数を $d(a, b)$ とする。
ある頂点 $x$ について、各頂点 $i$ の「割り当てられた値 $C_i$ × 頂点 $x$ と頂点 $i$ の間にある辺の数」の和を $f(x)$ とする。
$f(x)$ の最小値を求めよ。
すなわち、
$$
f(x) = \sum_{i=1}^N \left(C_i \times d(x, i)\right)
$$について、
$$
\min_{1 \leq v \leq N} f(v)
$$を求めよ。
解法
部分木を用いた f(x) の計算
$f(x)$ を計算するとき、頂点 $x$ を計算を行う木の根であるとみなすことにする。
さらに、この頂点 $x$ を根とする木について、頂点 $x'$ を根とする部分木に関する $f(x')$ を $f^*(x')$ とする。
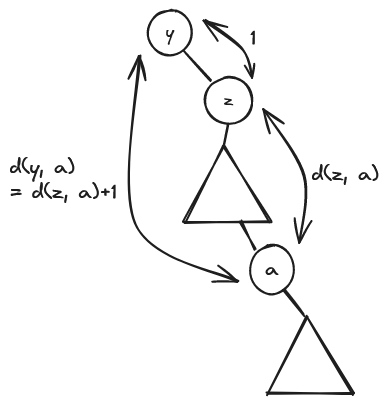
ここで、ある頂点 $y$ とその子である頂点 $z$ を考える。
頂点 $z$ を根とする部分木に含まれるある頂点 $a$ を考えると、頂点 $y$ と頂点 $a$ の間にある辺の数は、頂点 $z$ と頂点 $a$ の間にある辺の数よりちょうど $1$ 多い。
この性質は頂点 $z$ を根とする部分木に含まれる頂点すべてについて成り立つので、頂点 $y$ を根とする部分木に含まれる頂点 $a$ (ただし $a \neq y$) について、$f^*(y)$ を計算する際に $C_a$ に掛ける値は、$f^*(z)$ を計算する際に $C_a$ に掛ける値よりちょうど $1$ 多い。
「$C_a$ に掛ける値を $1$ 増やす」ことは、「$C_a$ を追加で1個足す」ことになる。
よって、$f^*(y)$ を求めるには、頂点 $y$ の子である頂点 $z$ それぞれについて、$f^*(z)$ に加え、頂点 $z$ を根とする部分木に含まれる頂点 $a$ に割り当てられた値 $C_a$ の和を加えればよい。
すなわち、頂点 $k$ の子である頂点の集合を $c(k)$、頂点 $k$ を根とする部分木に含まれる頂点の集合を $s(k)$ とすると、
$$
f^*(y) = \sum_{z \in c(y)} \left(f^*(z) + \sum_{k \in s(z)} C_k \right)
$$となる。
これを再帰関数で計算する際は、$f^*(y)$ の値とともに、計算を行っている部分木における $C_i$ の和を返すと計算しやすくなる。
具体的には、以下のようなアルゴリズムで計算できる。
def calc(x): # x : 計算を行う部分木の根である頂点
ans = 0 # f*(x) の値
csum = 0 # 部分木における C_i の和
for k in children(x): # 頂点 x の子である頂点について繰り返す
k_ans, k_csum = calc(k) # 子を頂点とする部分木について計算する
ans += k_ans + k_csum # f*(k) の値に、さらに各頂点の C_i (の和)を加える
csum += k_csum # C_i の和の情報を更新する
csum += C[x] # C_x を加え、x を根とする部分木に含まれる頂点すべての C_i の和を求める
return ans, csum # 結果を返す
メモ化
1個の頂点 $x$ について $f(x)$ を求めるのであれば、上記のアルゴリズムにより calc(x) を各頂点について一度ずつ呼び出すので、$O(N)$ で計算できる。
しかし、今回は $f(x)$ の最小値を求めたいので、すべての頂点についてそれぞれ $f(x)$ を求めると、$O(N^2)$ となり、間に合わない。
そこで、calc(x) をメモ化することで、計算の効率を上げることを考える。
なお、上記の calc(x) は頂点 x と繋がった頂点のうちどれが子であるか (すなわち、どれが子でない (親である) か) が固定されている表現になっているが、頂点 $x$ を変えて $f(x)$ を計算すると、各頂点の親となる頂点も変わりうることに注意したい。
「どこから来たか」でメモ化する (失敗)
各頂点 x における calc(x) の値をメモ化したいが、実際は同じ頂点 x であっても親となる頂点によって calc(x) の値は変化することが考えられる。
かといって、今いる頂点と親となる頂点の組をキーにしてメモ化しようとすると、$O(N^2)$ のメモが要求され、現実的でなさそうである。
ここで、「親となる頂点」は辺と関係が深いことに注目する。
各辺の両端のうち一方が「今いる頂点」となり、他方が「親となる頂点」となる。
したがって、各辺を有向とみなす (それぞれの向きを別の辺とみなす) と、各有向辺と「今いる頂点と親となる頂点の組」が一対一で対応する。
これらに根、すなわち親となる頂点が無い頂点として各頂点を使う場合も考えることで、頂点数 $N$ のだいたい3倍のメモがあればよいことになる。すなわち、メモの数は $O(N)$ ですむ。
しかし、これを実装して提出すると、TLEになってしまった。
提出 #52100242 - トヨタ自動車プログラミングコンテスト2024#4(AtCoder Beginner Contest 348)
よく考えると、それぞれのメモに書き込む値を求めるのに最大で $O(N)$ かかってしまい、計算量は $O(N^2)$ になってしまうことがわかる。
たとえば、巨大なウニのようなグラフを考えると、中央の頂点に向かう辺それぞれについて中央の頂点から出ていく辺の数の繰り返しが発生し、計算量が $O(N^2)$ になることがわかる。
隣接する全頂点についての和をメモする (失敗)
計算の仕方をよく観察すると、「その頂点にどこから来たか (親)」の情報は「親である頂点は子に関する繰り返しから除く」ためにのみ使っていることがわかる。
親となる頂点は0個または1個しか無いため、それぞれの親についてほとんど同じような繰り返しが発生してしまい、効率が悪い。
そこで、ある頂点に初めて訪れ、計算をする際、その頂点に隣接する全頂点についての和を求めてメモし、親が存在する場合は親に関する情報をメモした和から減算することで答えを求めることを試みた。
しかし、これを単純に行おうとすると、ランタイムエラーになってしまった。
(コードテストで気付いたため、提出はしていない)
これは、親である (来た元の) 頂点でも無条件で計算しに行くため、無限に往復することになってしまいうるためである。
上記2通りの戦略を組み合わせる (成功)
来た元の頂点があってもそこに進んだことが失敗の原因のようなので、これを行わないようにする機能を追加する。
これを行うため、各頂点についてメモの状態を以下の3種類で管理する。
- メモなし
- 不完全なメモあり
- 完全なメモあり
「メモなし」とは、その頂点に隣接する頂点に関する和の情報が全く無い状態である。
この場合は、隣接する頂点それぞれについて calc(x) の計算を行い、和を求める。
このとき、来た元の頂点 (親) がある場合は、繰り返し処理の対象から除く。
和を求めたら、求めた和をメモに記録する。
また、和だけでなく、それぞれの頂点に関する calc(x) の計算結果も記録しておく。
繰り返し処理の対象から除いた頂点がある場合は、それがどの頂点か (すなわち、どの頂点が親だったか) も記録し、メモの状態を「不完全なメモあり」にする。
除いた頂点が無い場合は、メモの状態を「完全なメモあり」にする。
いずれの場合も、求めた和をそのまま calc(x) の結果として返してよい。
「不完全なメモあり」とは、その頂点に隣接する頂点のうち1個だけを除いた和の情報がある状態である。
今回和を求めるにあたり、来た元の頂点 (親) がメモに記録されている除かれた頂点と同じである場合は、メモに記録されている和をそのまま calc(x) の結果として返してよい。
来た元の頂点が除かれた頂点とは違う、または存在しない場合は、まず除かれた頂点について calc(x) の計算を行い、結果をメモに記録されている和に加え、メモの状態を「完全なメモあり」にする。
続いて、来た元の頂点が存在する場合は、その頂点に関する calc(x) の計算結果を新しい和から減算し、calc(x) の結果として返す。
来た元の頂点が存在しない場合は、新しい和をそのまま calc(x) の結果として返す。
「完全なメモあり」とは、その頂点に隣接する頂点すべてに関する和の情報がある状態である。
来た元の頂点が存在する場合は、その頂点にその頂点に関する calc(x) の計算結果をメモに記録されている和から減算し、calc(x) の結果として返す。
来た元の頂点が存在しない場合は、メモに記録されている和をそのまま calc(x) の結果として返す。
この方法なら、各頂点について隣接する頂点に関する繰り返しは高々1回ですむ上、来た元の頂点には行かないので無限に往復してしまうこともない。
この方法により、ACを得ることができた。
提出 #52108472 - トヨタ自動車プログラミングコンテスト2024#4(AtCoder Beginner Contest 348)