何をするのか
点をランダムでサンプリングし、円の中に入った点の割合から円周率の値を推定します。 (モンテカルロ法)
原理
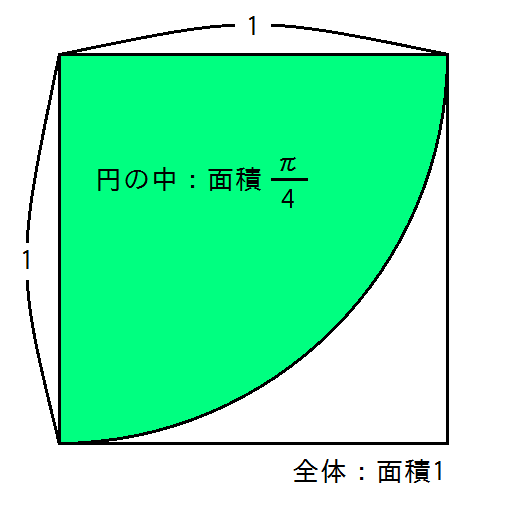
以下のような、正方形の中に円の4分の1の部分が入った図形を考えます。
この正方形の面積は、$1\times 1 = 1$です。
半径$r$の円の面積は$\pi r^2$なので、この図形の中の円の部分の面積は$\pi / 4$です。($r = 1$)
したがって、この正方形の中に一様ランダムに点を打っていくと、各エリアに入る確率は各エリアの面積に比例し、
円の中に入る確率は$(\pi / 4) / 1 = \pi / 4$となります。
これは、大量に点を打っていくと、(円の中に入った点の数)÷(打った点の数)≒$\pi / 4$となるということです。
この性質を用いると、円周率の値が(円の中に入った点の数)÷(打った点の数)×4で推定できます。
実行結果
ソースコード
10 'モンテカルロ ホウ
20 CLS:FOR I=0 TO 399
30 POKE#900+I/20*32+I%20,#80
40 NEXT:FOR Y=0 TO 39
50 B=1600-(Y+1)*(Y+1)
60 X=1:P=#900+Y/2*32
70 IF X*X>B GOTO 120
80 D=Y%2*3+1
90 IF (X+1)*(X+1)<=B D=D*3
100 POKE P,PEEK(P)|D
110 X=X+2:P=P+1:GOTO 70
120 NEXT:P=#900:D=0
130 C=0:FOR T=1 TO 3000
140 X=RND(10000):U=X/250
150 Y=RND(10000):V=Y/250
160 POKE P,PEEK(P)^D
170 P=#900+V/2*32+U/2
180 D=1<<(V%2*2+U%2)
190 POKE P,PEEK(P)^D
200 A=X/100:B=X%100
210 E=Y/100:F=Y%100
220 G=(B*B+F*F)/100
230 H=2*A*B+G:K=H/100
240 L=(H%100+2*E*F)/100
250 IF A*A+E*E+K+L<=10000 C=C+1
260 LC 0,21
270 ?C;"/";T;" PI=";C*4/T;".";
280 R=C*4%T:FOR I=1 TO 4
290 R=R*10:?R/T;:R=R%T
300 NEXT:?
310 NEXT
解説
ある点$(x, y)$が中心$(0, 0)$、半径$r$の円の周または内部(以下、円の中)にあるかは、
$x^2 + y^2 \leq r^2$を満たすかどうかで判定できます。
前半ではこの性質を利用し、右下が円の中にある点を白く塗っています。
後半がモンテカルロ法の本体で、この性質を利用してランダムに打った点が円の中に入ったかを判定しています。
上の原理では$1\times 1$の正方形を使いましたが、図形を拡大しても面積比は変わらないので、
プログラムでは$10000 \times 10000$の正方形を利用しています。($r = 10000$)
ここで、IchigoJamの変数は32,767までの数しか扱うことができないのに対し、$0 \leq x, y < 10000$であり、
$x^2 + y^2$は最大$2 \times {10000}^2 = 200,000,000$程度になるため、工夫が必要です。
今回は、以下のような工夫をしました。
まず、$x$および$y$を以下のように2桁ずつに分割します。
$$\begin{eqnarray*}
x &=& 100a + b \hspace{1em} (0 \leq a, b < 100)\\
y &=& 100c + d \hspace{1em} (0 \leq c, d < 100)
\end{eqnarray*}$$
すると、$x^2$および$y^2$は以下のようになります。
$$\begin{eqnarray*}
x^2 &=& {(100a + b)}^2 = 10000a^2 + 100\cdot 2ab + b^2 \\
y^2 &=& {(100c + d)}^2 = 10000c^2 + 100\cdot 2cd + d^2
\end{eqnarray*}$$
さらにこれらを足すと、
$$x^2 + y^2 = 10000(a^2 + c^2) + 100(2ab + 2cd) + (b^2 + d^2)$$
となります。
$0 \leq a,b,c,d < 100$より、$a^2 + c^2$、$2ab$、$2cd$、$b^2 + d^2$は$20000$以下なので、そのまま計算できます。
これらの値を用いて、以下の図のように下位から上位へ計算していきます。
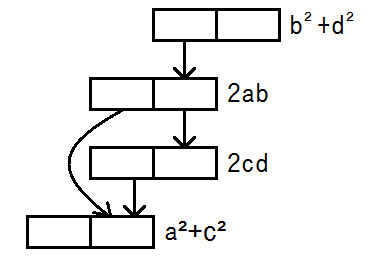
図中の2個つながった四角形は、右の四角形が十進数の下位2桁、左の四角形が残りの部分を表します。
値が確定した下位を切り捨てていくことで、扱える値の範囲で計算を行います。
最終的に、$a^2 + c^2$に下位からの繰り上がりを足した値が10000以下であれば点は円の中に入っている、
10000を超えていれば点は円の中に入っていない、と判定できます。
IchigoJamとは
2,000円前後で購入することができ、BASICによるプログラミングが可能なパソコンです。
こどもパソコン IchigoJam - はじめてのプログラミングパソコン(1500円)
また、プログラムをWebブラウザ上で実行できるサービスもあります。
※「IchigoJam」はjig.jpの登録商標です
