1つの母集団から抽出した標本から，母平均μ，母分散σを推定する方法

１．この記事でまとめたいこと

1つの母集団から無作為にn個の標本を抽出し，その標本から母集団の母数（平均$\mu$や分散$\sigma^2$）の区間推定を行う方法。絵でいうと下記。

２．まとめた背景

参考書などで勉強していたところ，下記のような色々なケースの区間推定の方法が出てきた。

• 母集団の分布・・・既知／未知
• 母分散・・・既知／未知

それぞれのケースで，新たに定義する確率変数や，その確率変数が従う分布（標準正規分布/t分布/カイ二乗分布）が異なっており，覚えられなかった。まとめていくと，共通する考え方が見えてきた。

３．共通する考え方

どれもこの①～③の流れで区間推定を行っている。

４．各ケースと共通する考え方に照らし合わせると

下図のように，全て共通する考え方で，区間推定を行うことができる。赤字がポイントだと思う。
図中の★部分は，５章で記載する。

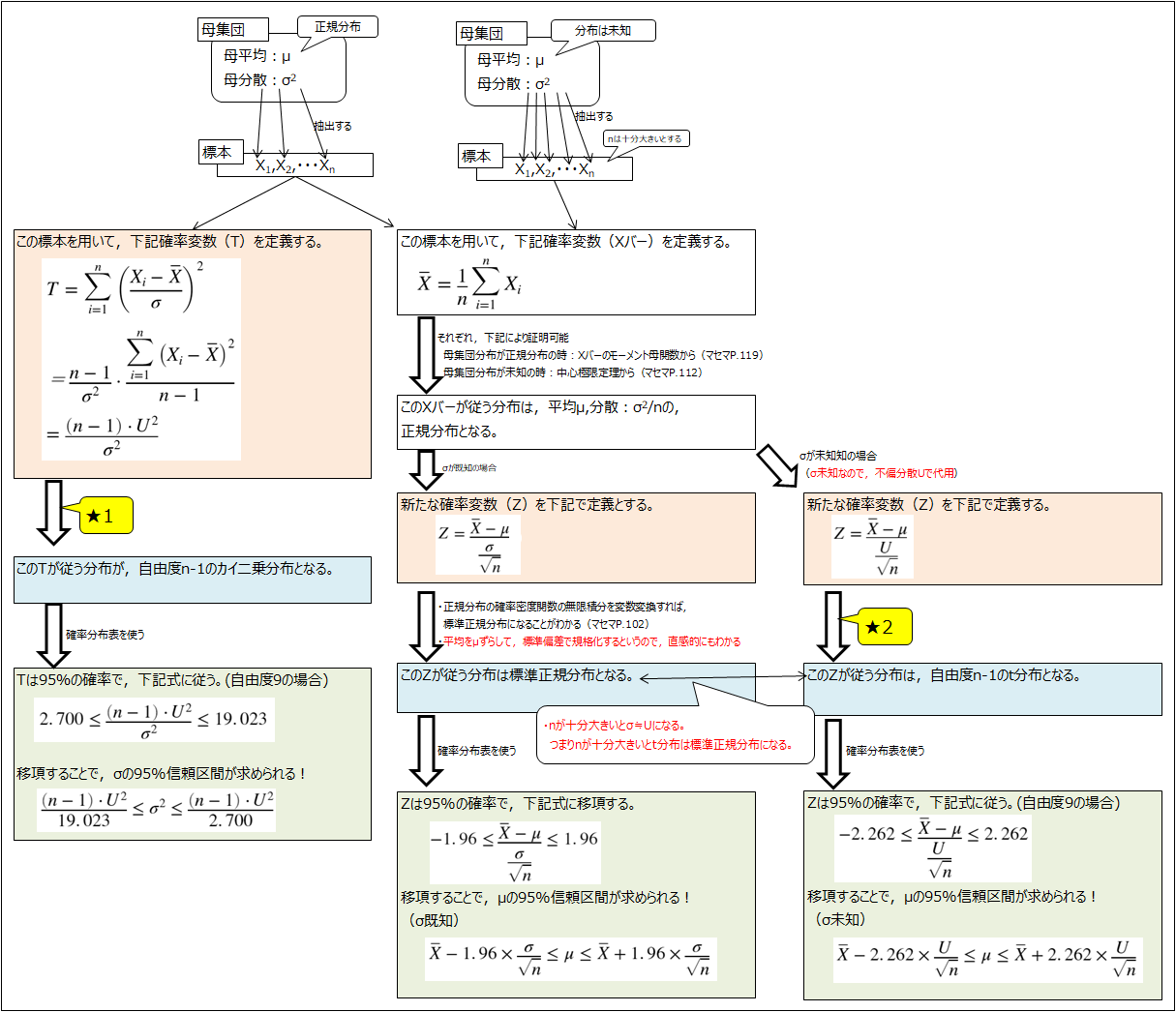
５．４章の図中の★部分についての説明

５．１．★１について

対比を取ると，このような感じになる。

標本平均を使うとなぜ自由度が1下がるのかについては，下記サイトで理解することができた。
@takayan4さん教えていただきありがとうございました。

・高校数学の美しい物語
https://mathtrain.jp/chinijoproof

５．２．★２について

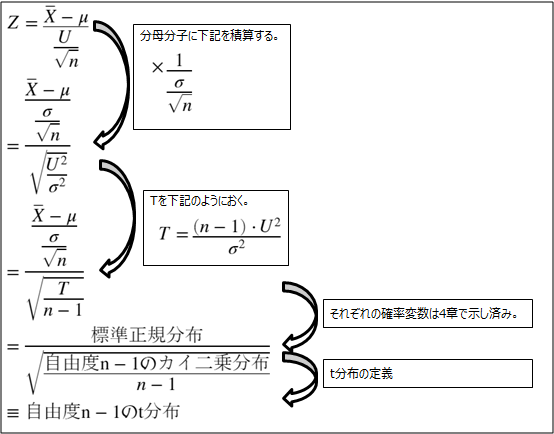
６．おまけ（確率密度関数）

関連する確率密度関数をMATLABでプロットしてみた。
本コードを実行するには，Statistics and Machine Learning Toolboxが必要です。

６．１．正規分布とt分布

t分布の自由度を増やすと，標準正規分布に近づいていく。
これは，nが大きくなると，不偏分散が母分散に近づいていくため。

Code

xrng = [-3,3];
fplot(@(x) normpdf(x,0,1),xrng,'DisplayName','Standard Normal Distribution') % 標準正規分布
hold on
fplot(@(x) tpdf(x,5),xrng,'DisplayName','t Distribution with \nu=5')      % 自由度5のt分布
fplot(@(x) tpdf(x,10),xrng,'DisplayName','t Distribution with \nu=10')    % 自由度10のt分布
legend
hold off

６．２．カイ二乗分布

Code

xrng = [0,20];
fplot(@(x) chi2pdf(x,1),xrng,'DisplayName','\nu=1') %自由度1のカイ二乗分布
hold on
fplot(@(x) chi2pdf(x,2),xrng,'DisplayName','\nu=2') %自由度2のカイ二乗分布
fplot(@(x) chi2pdf(x,3),xrng,'DisplayName','\nu=3') %自由度3のカイ二乗分布
fplot(@(x) chi2pdf(x,5),xrng,'DisplayName','\nu=5') %自由度5のカイ二乗分布
fplot(@(x) chi2pdf(x,10),xrng,'DisplayName','\nu=10') %自由度10のカイ二乗分布
legend
hold off

７．参考文献

・マセマ出版社　統計学キャンパス・ゼミ 改訂5
https://www.mathema.jp/product/統計学キャンパス・ゼミ-改訂5/

・ヨビノリ　確率統計　推定・検定入門
https://www.youtube.com/playlist?list=PLDJfzGjtVLHmx7qMP410-9gx0weC9d90X

・高校数学の美しい物語
https://mathtrain.jp/chinijoproof