この記事はfreeeデータに関わる人たち Advent Calendar 2019の4日目のエントリーです。
こんにちはfreeeのAnalyticsチームで分析基盤、機械学習基盤を作ったり、実際に分析している須貝です。この記事では統計的優位差と効果量の関係を可視化してみようと思います。途中ベイズっぽい用語と数式が出てきますが、多分スルーしても大丈夫です。
統計的有意差と効果量とは
色々な記事で取り上げられているので今回は詳しくは説明しませんが、少しだけ述べておきます。統計的な優位な差があったかどうかを確認する方法の一つに仮説検定があります。本記事では"z値"と"事後分布の比較"を扱います1。また統計的に優位だったとして、それがどれだけ効果があったのかを指すのが効果量です。分布によって使われる効果量は異なってくるのですが、例えば2項分布ではodds比やodds差、Relative risk2あたりが専門家以外にも説明しやすいかと思います。他にはどのようなものがあるかをざっくり知りたい場合は英語版wikipediaを参照するといいと思います。
細かいことはいいのでさっさと可視化する
下準備
ECサイトの広告を運用していて新しい施策をA/Bテストで評価することを考えます。このとき広告が表示された回数を$N$、その広告をクリックした回数を$n$、CTRを$p=n/N$と置きます。施策を適用したグループをB、何も変更しないグループをAとし、グループごとの値を$N_A$などと表記します。
またz値を
z = \frac{n - N p}{\sqrt{n p(1 - p)}}
で計算します。有意水準を$\alpha=0.05$とし、統計数値表からの$Z_{0.025}$の値を読み取ると1.96なので、この値よりも大きいかどうかで有意か否かを見ていきます3。
またMCMCで各グループで事後分布からサンプリングして次の値を計算します。
u^{(i)} =
\begin{cases}
1 & \text{ if } \ \ p_B^{(i)} > p_A^{(i)} \\
0 & \text{ else }
\end{cases}
P(p_B > p_A) = \frac{1}{N} \sum_{i}^{N} u^{(i)}
どれだけ事後分布が重なり合っているかを示していると思えば大丈夫です。
あとは効果量をRelative riskを $R=p_B\ /\ p_A$ とします。
パターン1: 試行回数が少なく、確率も似通っているとき
| 表示回数(N) | クリック数(n) | CTR(p) | |
|---|---|---|---|
| 条件A | 1,000 | 10 | 0.01 |
| 条件B | 1,000 | 11 | 0.011 |
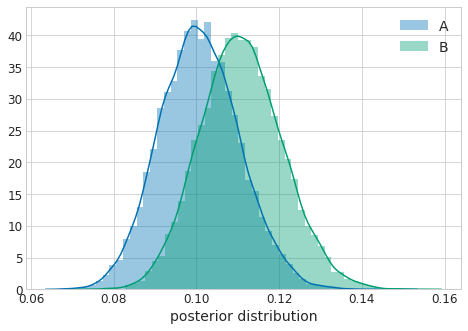
この結果をStanで2項分布でモデリングし、20,000ほど事後確率をサンプリングするとCTRの事後分布は以下のようになります。分布がある程度4重なっているのがわかります。
この各20,000のサンプルから $P(p_B > p_A)$ を計算したところ $P(p_B > p_A) = 0.59$ と出ました。施策を実施したほうが59%の確信でCTRは上がります。あまり自信を持ってこの施策を進められませんね。このときz値を計算すると$z=0.31$と出たので、有意水準を下回り、帰無仮説を棄却できませんでした。またこのときRelative riskは$R=0.011/0.01=1.1$です。
パターン2: 試行回数が少ないが、確率は差があるとき
| 表示回数(N) | クリック数(n) | CTR(p) | |
|---|---|---|---|
| 条件A | 1,000 | 10 | 0.01 |
| 条件B | 1,000 | 30 | 0.03 |
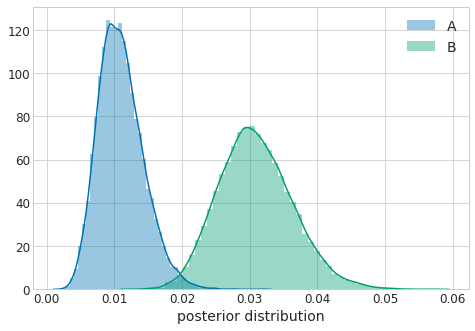
同じくモデリングした結果が以下になります。分布の重なりが少ない4のがわかります。
同じく$P(p_B > p_A)$ を計算すると $P(p_B > p_A) = 0.99.. \simeq 1.0$でした。z値は$z=6.36$で有意水準を上回り、帰無仮説を棄却できました。またこのときRelative riskは$R=0.03/0.01=3.0$です。
パターン3: 試行回数が多いが、確率は似通っているとき
| 表示回数(N) | クリック数(n) | CTR(p) | |
|---|---|---|---|
| 条件A | 1,000,000 | 10,000 | 0.01 |
| 条件B | 1,000,000 | 11,000 | 0.011 |
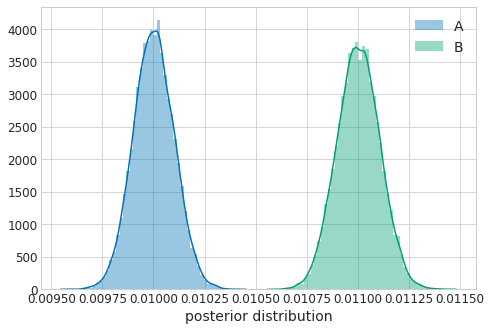
同じくモデリングした結果が以下になります。パターン2と同じく、分布の重なりが少ない4のがわかります。またパターン2よりも事後分布が収束しているのがわかります。
同様に色々計算すると$P(p_B > p_A) = 1.0$でした。z値は$z=10.0$で有意水準を上回り棄却しました。またこのときRelative riskはパターン1と同じく$R=1.1$です。
まとめと考察
以上から少ないサンプルでも効果量が大きいときは有意差がありますし、効果量が小さく5てもサンプルサイズを増やしていけば有意差がでることがわかりました。当たり前といえば当たり前なのですが、その割には初心者向けの効果量の説明が少なかったりして、検定だけしておしまい、みたいな人が増えないように書いてみました。