最近、ニュースなどで「機械学習」や「AI」といったフレーズを耳にすることも増えてきたのではないでしょうか。ただ、数学的な方法をベースにしながらモノを考えるといっても、実際にどう使えばよいだろうとピンと来ない方のほうが多いのではないでしょうか。コンピュータの世界で数学がどのように使えるのか、ということをPythonの基本的な書き方を確認しながら考えていきたいと思います。
「数学的な問題をPythonで簡単なスクリプトを作って動作を確認する」ということを複数回に分けて行っていきたいと思います。Pythonに慣れるという点でも手を動かして考える機会にして頂ければ幸いです。
今回は、Pythonで学び直す数学【集合・確率編】の確認をしていきたいと思います。
演習問題のダウンロードはこちらから

数学の授業で、「確率を求めるときに、図や一覧表を描いたり、ベン図や集合の要素数を利用して、場合の数を求め、全体でどれだけの数があるか正しく把握してください」と習った方も多いと思います。ここでは今一度、集合の基礎から学んでいきましょう。
まずは、集合の特徴についてみていきます。
・集合の定義
数学の世界で「1から10までの自然数」の集合は、A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
のように { } を使って表記します。
「A」は集合に付けた名前で、 { } に含まれる個々の値を要素といいます。
1つの集合に同じ要素が含まれることはなく、また、集合の要素には順番という概念がありません。
下のように「1から10までの自然数」の集合を考えた場合、
B = {2 ,5, 6, 7, 1, 3, 4, 9, 10, 8}
集合Aと集合Bは同じものとして扱われます。
< Type Python >
Pythonにはset という集合を扱うデータ型があります。
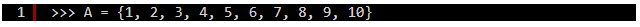
のようにすると、集合Aを定義できます。
集合Aの要素の順番を変えて、集合Bを定義して集合Aと比べてみましょう。

もう一つ、集合の要素には重複した値が含まれないことも確認しておきましょう。

len() 関数を利用すると、集合の要素数を確認できることも覚えておきましょう。
・全体集合、部分集合
集合Aのすべての要素が集合Uに含まれるとき、集合Aを集合Uの「部分集合」といい、 U⊃A のように表します。Pythonでは「<=」を使って部分集合かどうかを確認することができます。

部分集合が属する集合Uのことを全体集合といいます。
・集合演算(和集合・積集合・差集合)
・和集合
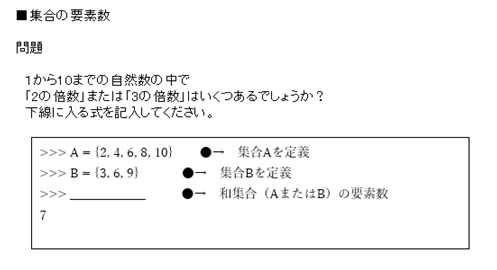
2つの集合の全要素を合わせた集合を和集合といい、
A∪B
のように表します。Pythonでは、|演算子を使って和集合を取得できます。

・積集合
2つの集合に共通する要素の集合を積集合といい、
A∩B
のように表します
Pythonでは、「&演算子」を使って積集合を取得できます。

・差集合
一方の集合から、もう一方の集合を引いたものを差集合といいます。
どちらの集合から引くかによって結果が変わるので注意してください。
Pythonでは、算術演算子の「-演算子」を使って差集合を取得できます。

⇒ ここで、添付資料「集合の要素数」シートにある演習問題を解いてみましょう
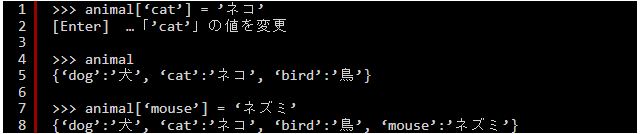
類似するケースとして、Pythonでの辞書, リストの使い方について確認していきましょう。

辞書(dictionary)とは、「キー:値」をカンマで区切って並べ、全体を「{}」で囲み、1組のデータをキーとそれに対応するペアで管理するデータ型です。
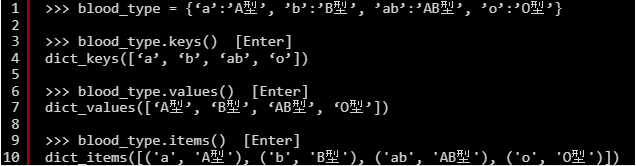
keys()、values()、items()メソッドの戻り値は、for文で順に取得できます。

参考:formatメソッドは変数の値を埋め込みたい時などに使われます。
例えば ‘str1{}:{}str2’.format(var1, var2) では、
1番目の{} にメソッド引数のvar1 が、2番目の{}にメソッド引数のvar2が埋め込まれます。
⇒ ここで、添付資料「辞書の使い方」シートにある演習問題を解いてみましょう


次は、図や一覧表を描いたり、ベン図や集合の要素数を利用したりして、場合の数の例題を解いていきましょう。
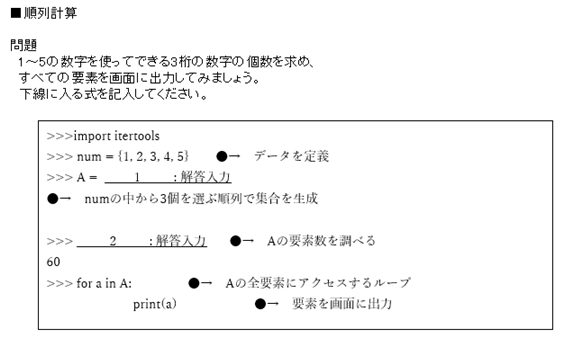
順列:n個のものからr個(r ≤n)を選んで並べる並べ方 nPr は
nPr = n (n-1) (n-2) … (n-r+1) = n! / (n-r)! (通り)
たとえば、1~9の9種類の数字を使ってできる2桁の数字は 9×8 = 72 (通り)
Pythonでは、以下のように求めることができます。

⇒ ここで、添付資料「順列」シートにある演習問題を解いてみましょう
⇒ ここで、添付資料「階乗」シートにある演習問題を解いてみましょう
組み合わせ:n個のものからr個を選び出す組み合わせ nCr は
nCr = nPr / r! = n! / r! (n-r)! (通り)
たとえば、1~5の5種類の数字から2つの数字を選ぶ組み合わせは 5×4 / 2×1 = 10(通り)
組み合わせが何通りかを調べるときは、itertoolsモジュールのcombinations() 関数を使います。
1~5のうち、2個の数字を選んだ場合は以下のようになります。

⇒ ここで、添付資料「組み合わせ」シートにある演習問題を解いてみましょう

次は確率(ある試行を行ったとき、結果として起こりうる全ての事象のうち、特定の事象になる割合)について考えてみましょう。
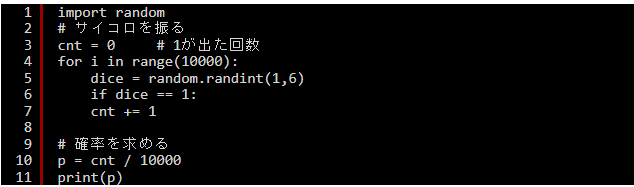
サイコロを振った時の特定の目が出る確率について、「大数の法則」という、試行の数が多ければ、確率は収束するという話を数学の授業で聞いたこともあるのではないでしょうか。
今回は実際に確認してみましょう。
以前学校で学んできた内容をもとにPythonでスクリプトを実行しながら確認できるのは面白いなと感じる方もいらっしゃるかもしれません。自分にできる範囲のものから少しずつPythonにも挑戦してみようかなと思っていただければ幸いです。
以上となります。
参考文献:
・大津真『基礎Python: 入門から実践へステップアップ』インプレス(2016年)
・谷尻かおり『文系プログラマーのためのPythonで学び直す高校数学』日経BP社(2021年)