初Qiitaにていきなりアドベントカレンダーです。
最近Graph Convolution界隈が盛り上がっているようですがすでに書かれている方がいらっしゃる(そもそも私にそこの知識はない)ようなので、ここではGraph Embeddingの手法について知識の整理もかねておさらいしていきます。
なお今回は基本的に無向グラフについて扱っていきます。
記載に誤り・誤解を招く表現がありましたらコメントにてご指摘お願いします。
(2018/12/31 Node2Vec部分追記しました)
今回扱うのは
・DeepWalk
・LINE
・Node2Vec
の3つです。
1. DeepWalk
論文はこちらです→Deepwalk: Online learning of social representations
DeepWalkがやっていることはすごくシンプルでNLPで用いられているSkipGramをそのままグラフに応用しただけです。
ただしグラフ構造のデータにSkipGramモデルをそのまま適用することはできないため、__Random Walk__という方法でデータを生成してからSkipGramモデルにかけます。
Random Walk
Rnadom Walkではそれぞれの頂点からランダムに出発し、そこで得られた頂点の組み合わせをNLPでいう文章のように扱います。
ある頂点$v_i$から出発して得られた頂点$v_1, v_2, ..., v_{i-1}$という条件のもと次の頂点$v_i$を観測する確率を以下のように考えます。
Pr(v_i\ |\ (v_1, v_2, ..., v_{i-1}))
しかしここでは共起の確率だけでなく潜在表現を学習することも目的とされています。
そこでマッピング関数$\Phi:v \in V \mapsto R^{|V| \times d}$を用いることで求めたい式を以下のように書きます。
Pr(v_i\ |\ (\Phi(v_1), \Phi(v_2), ..., \Phi(v_{i-1})))
例えばここでいう$\Phi(v_1)$は頂点$v_1$の潜在表現です。
しかしながらRandom Walkする長さが大きくなった場合$\Phi(v_i)$を全て計算するには大きなコストがかかります。
ですが
Efficient Estimation of Word Representations in Vector SpaceやDistributed representations of words and phrases and their compositionalityにて説明されているように
1. 文脈から単語を予測するのではなく単語から予測する
2. 文脈は対象の単語の前後に現れるものとする
3. 単語の順序を無視する代わりに前後の文脈を無視して予測したい単語が出現する確率を最大化する
という条件の緩和を行うことで
minimize_\Phi - \log{Pr} (\{v_{i-w}, ..., v_{i+w}\}\ /\ v_i\ |\ \Phi(v_i))
を最適化するよう問題を書き換えることができます。1
DeepWalkの大まかな流れ
改めて流れを整理すると以下のようになります。
1. 潜在表現$\Phi$を初期化
2. Random Walkにより頂点の集合$(v_1, v_2, ..., v_{i})$を獲得
3. SkipGramモデルにて重みを更新していく
SkipGramモデルについては他に詳しく説明してある記事がありますのですみませんが割愛します(例えばこことか)。
なおここではnegative samplingではなくhierarchical softmaxを用いていることに注意する必要があります。
2. LINE
論文はこちらです→LINE: Large-scale Information Network Embedding
LINEではローカルな構造(first-order proximity)とグローバルな構造(second-order proximity)のいずれも最適化するようモデリングされています。
ここでいきなりfirst order proximityとsecond order proximityという2つの単語が出てきましたのでこれらを説明します。
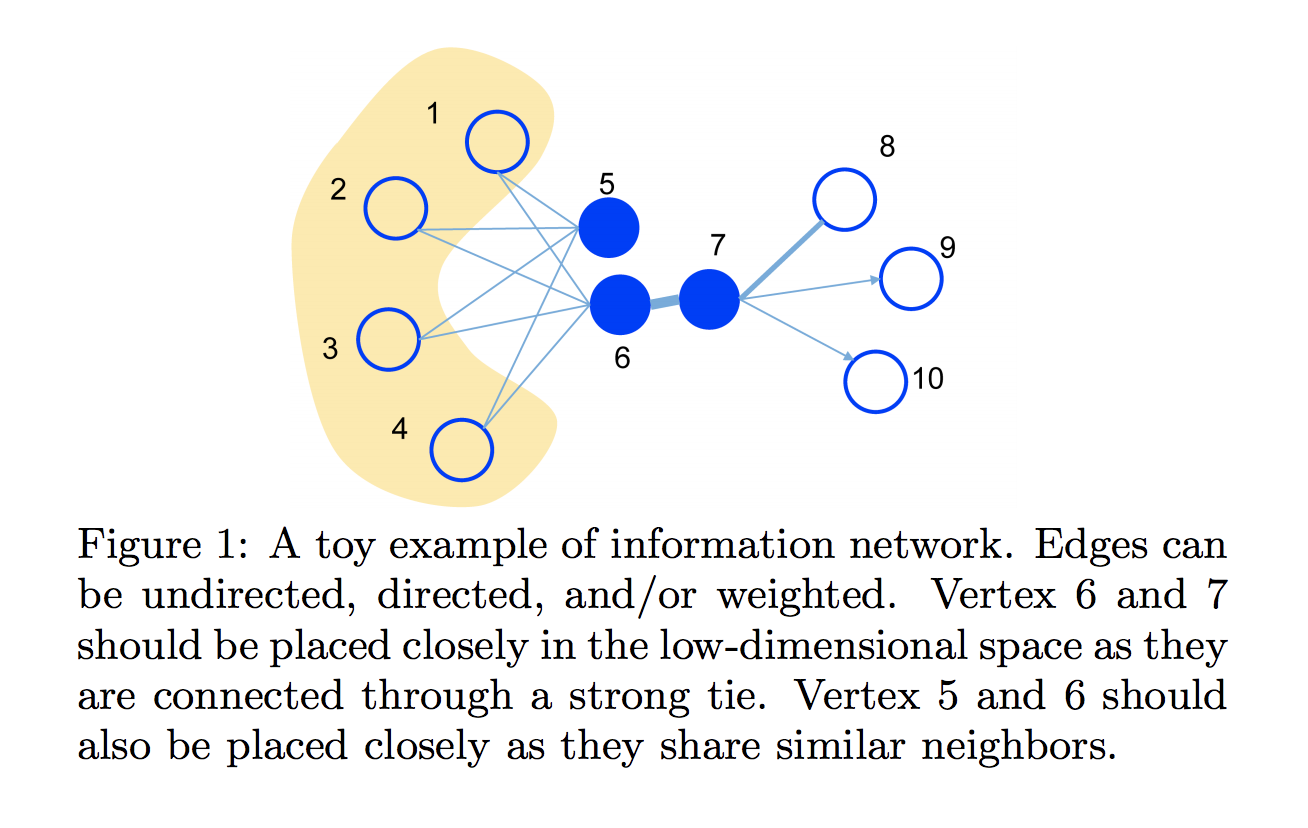
__first-order proximity__は直接的に観測される頂点v同士の近接性のことをいい、下の図でいうノード5 vs ノード1~4の部分に当たります。直接繋がっているから近しいという見方です。
一方__second-order proximity__は同じような頂点が近接している構造をもつ頂点同士の近接性のことをいいます。
下の図でいうとノード5とノード6はいずれもノード1~4と繋がっているため構造的に近しいといいます。
以下first-order proximityとsecond-order proximityについてそれぞれ定式化していきます。
first-order proximity
まず頂点$v_i$と$v_j$の同時確率は以下のように表現されます
p(v_i, v_j) = \frac{1}{1 + \exp(-\vec{u_i} ^T.\vec{u_j})}
ただし$\vec{u_i}\in R^d$は頂点$v_i$の低次元ベクトル表現です。
$w_{i,j}$をエッジに対する重み、$W = \sum_{i,j\in E} w_{i,j}$としたとき統計的な確率は$\hat{p_1}(i,j)= \frac{w_{i.j}}{W}$となります。
あとは以下の式を最適化するだけです($d$は二つの確率分布の距離)。
O_1 = d(\hat{p}_1(.,.), p_1(., .))
なお$d(., .)$をKLダイバージェンスで置き換え定数を除くと
O_1 = - \sum_{(i,j)\in E} w_{ij} \log p_1(v_i, v_j)
なおfirst-order proximityが当てはまるのは無向グラフのみである点にも注意が必要です。
second-order proximity
上で述べた通りsecond-order proximityは共通している他の頂点が似ているほど(=構造が似ているほど)2つの頂点を近しいものとします。
これを表現するためにここでは$\vec{u_i}$と$\vec{u_i}'$という2つのベクトルを以下のように考えます。
- $\vec{u_i}$ ... 頂点$v_i$の表現
- $\vec{u_i}'$ ... 頂点$v_i$の文脈(context)としての表現
以上を用いて$v_i$という条件のもとでの文脈(context)$v_j(i\neq j)$の確率を以下のように示します。
p_2(v_j|v_i) = \frac{\exp(\vec{u_j} ^T. \vec{u_i})}{\sum_{k=1}^{|V|}\exp(\vec{u'_k} ^T.\vec{u_i})}
ここにおける$|V|$は頂点でありcontextの数のことを言います。
そしてsecond-order proximityを最適化する式は以下のように導かれます。
O_2 = \sum_{i\in V} \lambda_i d(\hat{p}_2(.|v_i), p_2(.|v_i))
first-order proximityと同様$d(., .)$をKLダイバージェンスで置き換え定数を除くと
O_2 = - \sum_{(i, j)\in E}w_{ij}\log{p_2}(v_j | v_i)
となります。
first-order proximityとsecond-order proximityの両方を保持したまま最適化するためにはこれらをそれぞれ計算した後concatします。
最適化に関するあれこれ
$O_2$の最適化に関する話です。
最後の式を最適化しようとする場合全ての負例$v_i$について計算を行うためかなりコストが高いです。
そのためここではnegative samplingを用いて計算の負荷を減らします。最後の式をnegative samplingにすることで各エッジ$(i, j)$の最適化関数を以下のように書けます。
\log{\sigma(\vec{u'_j}^T . \vec{u_i})} + \sum_{i=1}^{K}E_{v_n \sim P_n (v)} [\log{\sigma}(- \vec{u'_n} ^T . \vec{u_i} )] \\
where \ \ \sigma(x) = \frac{1}{1 + \exp(-x)}
最適化にはasynchronous stochastic gradientを用いており、それぞれのステップにおける頂点iのembeddingベクトルは以下のように計算されます。
\frac{\partial O_2}{\partial \vec{u_i}} = w_{ij}. \frac{\partial \log{p_2}(v_j|v_i)}{\partial \vec{u_i}}
この記載のとおりエッジのウェイト$w_{ij}$が計算に使われているのですが、この分散が大きくなればなるほど学習率の調整が難しくなります。
この問題に対処するためサンプリングの手法にalias sampling methodを用いそれにより計算効率を改善しました。2
3. Node2Vec
論文はこちら→node2vec: Scalable Feature Learning for Networks
Node2Vecの基本的な構造はDeepWalkと同じですがサンプリング方法に違いがあります。
ここで起点ノード$u$から生成された近傍ノードの集合を$N_s (u)$、 特徴量の表現を$f(u)$として定義すると、目的関数は以下のように示されます。
max_s \sum_{u in V} \log Pr(N_s (u) | f(u))
ここの$N$についている$s$はサンプリング方法の戦略で、これについては後ほど触れます。
さらに2つ仮定をおきます。一つはある近傍ノードを選ぶ際の確率は他の近傍ノードを選ぶ確率とは独立であるとし、
Pr(N_s (u) | f(u)) = \prod_{n_i \in N_s (u)} Pr(n_i | f(u))
とします。また特徴量同士は対象的であるとし、ソフトマックスにて用いられるノードの組み合わせの見込みはそれぞれの特徴量ドット積で表されるとし、以下のように定義されると仮定します。
Pr(n_i | f(u)) = \frac{exp(f(n_i) . f(u))}{\sum_{v \in V} exp(f(v) . f(u))}
以上2つの仮定を元に元々の目的関数は以下のように書き換えられることができます。
max_f \sum_{u \in V} [- \log Z_u + \sum_{n_i \in N_S(u)} f(n_i ) . f(u)]
ここの$Z_u = \sum_{v \in V} exp(f(u) . f(v))$を計算するにはかなりコストが掛かるため、これまで同様negative samplingを用いて計算していきます。
BFSとDFS
Node2Vecの主題であるサンプリング方法の話です。
単なるRandom Walkではグラフ上のノードが(近隣にあるもののうち)ランダムに取得されていくわけですが、ここではその取得の方法をもっとグラフらしくしようという取り組みをしています。
そこでサンプリングの方法として__Breadth-first Sampling(BFS)__と__Depth-first Sampling(DFS)__の2つが挙げられています。
これらはそれぞれ以下のように説明されています
-
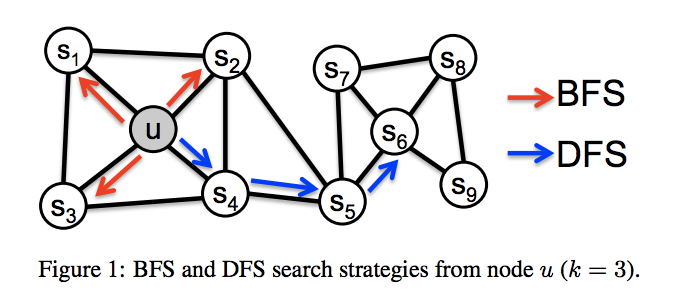
Breadth-first Sampling
→近傍$N_s$を実際に近接しているノードに限定する方法。例えば下の図の$s_1 \sim s_3$が該当 -
Depth-first Sampling
→近傍をより遠くのノードから構成する方法。下の図でいう$s_4 \sim s_6$が該当。
これらはどちらかが良いというタイプのものではなく使い分けが必要になります。
たとえばBFSばかりを重視してしまうと近隣の関係しか表現しきれず、DFSばかりを重視してしまうと得られたグラフのノードたちが起点のノードを表現しているのか怪しくなってしまいます。
つまりここではBFSとDFSをコントロールできるようRandom Walkを修正していくことになります。
そこでまず直前のノード$c_{i-1}$が得られたときに次にノード$c_i$が得られる確率を以下のように表現します。
P(c_i = x | c_{i-1} = v) = \left\{
\begin{array}{ll}
\frac{\pi_{vx} }{Z} & (if(v,x) \in E) \\
0 & (otherwise)
\end{array}
\right.
$\pi_{xv}$はノード$x, v$の遷移確率(unnormalized transition probability)で、$Z$は正規化のための定数です。
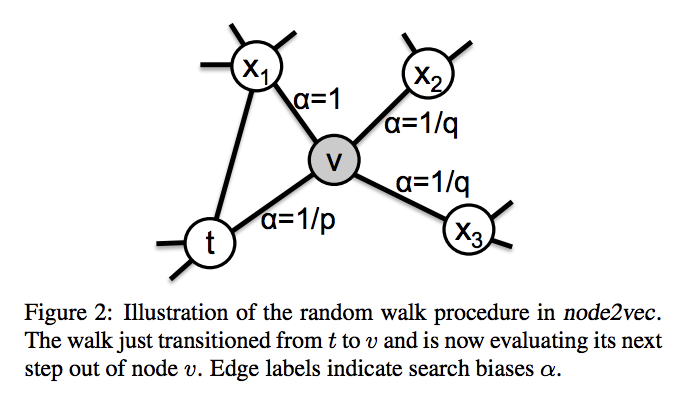
ここであるノード$t$から$v$へ遷移したとしそこからどのように遷移するかについて考えてみます(以下の図参照)。
ここでノード$t$からノード$x$への最短距離$d_{tx}$に応じて$\pi_{xv} = \alpha_{pq} (t,x).w_{vx} $が決定されるとすると、
\alpha_{pq} (t,x) = \left\{
\begin{array}{ll}
\frac{1}{p} & (if d_{tx} = 0) \\
1 & (if d_{tx} = 1) \\
\frac{1}{q} & (if d_{tx} = 2) \\
\end{array}
\right.
と表されます。
このように決定される$\alpha_{pq} (t,x)$のことをサーチバイアスといい、Node2Vecでは__return parameter__である$p$と__In-out parameter__である$q$を調節することでノードのサンプリング方法を調整していきます。
ここまで終えてしまえばあとはほとんどRandom Walkと同じです。
(なお実際にはこの後さらにalias samplingを入れてから勾配を調整していきます)
以上です。
今回紹介した論文
- Grover, Aditya and Leskovec, Jure “node2vec: Scalable Feature Learning for Networks” Proceedings of the 2second ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2016.
- Perozzi, Bryan, et al. "Deepwalk: Online learning of social representations" Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2014.
- Tang, Jian, et al. “LINE: Large-scale Information Network Embedding”, Proceedings of the 24th International Conference on World Wide Web, 2015
(GitHub: https://github.com/tangjianpku/LINE)