初心者がAIモデルで株価予測してみた #Python3

はじめに

2024年2月より、Aidemy premiumにて「データ分析講座6ヶ月コース」を受講しました。
育休中にスキルアップをして復職後の仕事の質を高めたい、そして働き方の選択肢を増やしたいと考えたのがきっかけでした。

本記事の概要

約半年間学んだ内容のアウトプットを目的としています。今回はハードルは高く設定しすぎず、基礎を大切に、まずは完成させることを第一にしています。
SARIMAモデルを用いた時系列分析を行い、株価予測をします。今回は資生堂の株価データのうち終値のデータを用い、以下の２パターンの分析を行います。
1. 日別データから算出した月平均データを用いて構築したモデルからの予測
2. 週別データを用いて構築したモデルからの予測

実行環境

Python 3.10.12
Google Colaboratory

株価予測の実装

その1. 日別データを月平均にならして利用

Yahoo!ファイナンスから取得した資生堂の日毎の株価データのうち終値を、月平均のデータに加工して用います。ここでは2019年1月〜2023年12月のデータから予測モデルを構築し、2023年1月〜2025年12月の株価を予測してみることにします。

1. 使用するライブラリをインポート

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import yfinance as yf
import statsmodels.api as sm
import itertools

2. 株価データの取得

Yahoo!ファイナンスから、資生堂（銘柄コード4911）の2019年1月〜2023年12月の日別の株価データを取得し、データの中身を確認します。

df = yf.download("4911.T", start="2019-01-01", end="2023-12-31", interval="1d")
df

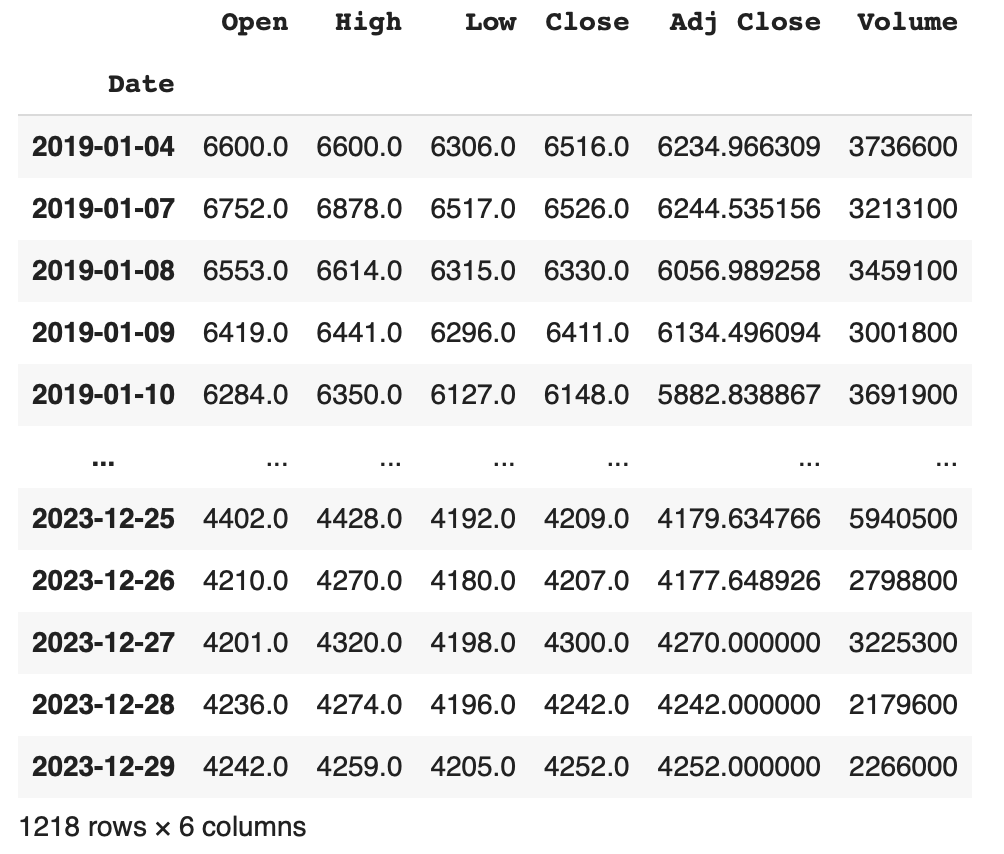
次に欠損値の確認を行います。

#欠損値の確認
df.isnull().sum()

欠損値がないことが確認できたので、このデータをこのまま使用します。

次に、今回使用する終値(Close)の値を抽出し、グラフで可視化します。

#1ヶ月毎（月平均）のデータに変更
df = df.resample(rule = "M").mean()
#グラフにして可視化
plt.plot(df["Close"])
plt.title("Close Price History of Shiseido")
plt.xlabel("Date")
plt.ylabel("Close price")
plt.show()

3. 自己相関係数・偏自己相関係数とその可視化

#自己相関・偏自己相関の可視化
fig=plt.figure(figsize=(9, 7))

#自己相関係数のグラフを出力
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df["Close"], lags=12, ax=ax1)

#偏自己相関係数のグラフを出力
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df["Close"], lags=12, ax=ax2)

plt.show()

コレログラムから、周期性はないと言えます。

4. 定常性の確認

原系列は、【トレンド + 季節変動 + 残差】に分解することができます。
つまり残差は、原系列からトレンドと季節変動が取り除かれた定常性のある時系列データになっています。

#季節調整を行い、原系列をトレンド、季節変動、残差に分けて出力する
sm.tsa.seasonal_decompose(df["Close"], period=12).plot()
plt.show()

グラフの上から原系列、トレンド、季節性、残差を表しています。
グラフより、右肩下がりのトレンドと、季節性があることが分かります。

5. モデルとパラメーターの決定

上記より、取得した株価データにはトレンドと季節性があることが分かったので、SARIMAモデルを用いて分析を行いたいと思います。
Pythonには、SARIMAモデルのパラメーター(p, d, q) (sp, sd, sq, s)の最も適切な値を自動で算出する機能はないので、情報量規準 (今回の場合は BIC(ベイズ情報量基準) )によってどの値が最も適切なのか調べるプログラムを書く必要があります。

下記のコードでは、時系列データ:DATA, パラメーターs(周期):sを入力すると、最も良いパラメーターとそのBICを出力します。
各パラメーターがそれぞれ、0,1の場合についてのSARIMAモデルのBICを計算し、最もBICが小さくなった場合を表示するようになっています。
今回はパラメーターsは12とします。

#関数の定義
def selectparameter(DATA,s):
    p = d = q = range(0, 2)
    pdq = list(itertools.product(p, d, q))
    seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
    parameters = []
    BICs = np.array([])
    for param in pdq:
        for param_seasonal in seasonal_pdq:
            try:
                mod = sm.tsa.statespace.SARIMAX(DATA,
                                            order=param,
                                            seasonal_order=param_seasonal)
                results = mod.fit()
                parameters.append([param, param_seasonal, results.bic])
                BICs = np.append(BICs,results.bic)
            except:
                continue
    return parameters[np.argmin(BICs)]

selectparameter(df["Close"],12)

6. モデルの構築

最適なパラメータ(p,d,q),(sp,sd,sq,s)が算出できたので、モデルを構築していきます。
確認のため構築したモデルのBICを出力し、パラメーター算出の際に出力したBICと一致することを確かめます。

#モデルの構築
SARIMA_close = sm.tsa.statespace.SARIMAX(df["Close"],order=(0, 1, 1),seasonal_order=(0, 1, 1, 12)).fit()
print(SARIMA_close.bic)

7. データの予測とその可視化

6で構築したモデルを用いて、2023年1月〜2025年12月の株価の終値を予測します。

#2023年1月〜2025年12月の終値を予測し、predに格納
pred = SARIMA_close.predict('2023-1', '2025-12')

#predと元の時系列データを可視化
#予測データは赤色で表示
fig=plt.figure(figsize=(10,6))
plt.title("Prediction of Close Price (monthly)")
plt.plot(df["Close"])
plt.plot(pred, "r")
plt.show()

下のグラフの青線が実績値（取得した株価データのうち終値の月平均）、赤線が得られた予測値です。

実績データと予測データのどちらもある2023年の1年間のデータに注目して比較してみると、
予測データの方がやや激しく上下していたり、多少のタイムラグがあったりするものの、グラフの形状は概ね合致しています。

その2. 週毎の株価データを取得して利用

同じ資生堂の株価データですが、データ取得の際のインターバルを1d（日毎）から1wk（週毎）に変えて試してみました。
というのも、上の予測結果で実績値と予測値の間にタイムラグがあったのは、データを月平均に加工して使用したのが一因としてあるのでは？と考えたからです。
株式市場は年中無休ではないため、年間365日のデータがあるわけではないという理由から、日別の株価をSARIMAモデルで予測することはできず（トライしましたがエラーが出てできませんでした）、取得した日別の株価データから月平均の終値を算出して使用しました。
今回はデータ取得の時点から日別ではなく週毎のデータを取得し、週毎の終値を使用してモデル構築と予測を行い、予測精度が高まるかどうかをみていきたいと思います。
流れは同じなので、異なるところのみ記述します。

1. 株価データの取得

引数のintervalを"1d"から"1wk"に変更することで、週毎のデータを取得できます。

df = yf.download("4911.T", start="2019-01-01", end="2023-12-31", interval="1wk")
df

2. パラメーターの決定

上で定義した関数selectparameter(DATA,s)を用いて算出します。
ここではs=52 (12ヶ月≒52週)とします。

#パラメーターの決定
selectparameter(df["Close"],52)

3. モデルの構築と予測・可視化

#モデルの構築
SARIMA_close = sm.tsa.statespace.SARIMAX(df,order=(0, 1, 0),seasonal_order=(1, 1, 1, 52)).fit()

#2023年1月〜2025年12月の終値を予測し、predに格納
pred = SARIMA_close.predict("2023-01", "2025-12")

#predと元の時系列データを可視化
#予測データは赤色で表示
fig=plt.figure(figsize=(10,6))
plt.plot(df)
plt.plot(pred, "r")
plt.show()

先に出した月平均のグラフと比較すると、2023年の1年間は実績値と予測値の乖離が、週毎のデータの方でより小さくなっていることが見て取れます。

ちょっと答え合わせ

ちなみに、分析には用いなかった2024年1月〜6月までの実績データもグラフにプロットして、答え合わせをしてみました（下記グラフのグレー背景部分）。
モデル構築時にも用いた2023年のデータとは違い、実績値と予測値の乖離が大きくなっています。SARIMAモデルによる予測ではあまり大きな山はなく推移していますが、実績では予測よりも大きな幅で株価が上昇しています。

おわりに

今回はSARIMAモデルを用いた時系列分析で株価予測を行いましたが、株価は時系列以外の様々な要素にも影響を受けているので、時系列分析だけでは高精度の予測を行うことは難しいと感じました。
今後も学習を続けて他のモデルを試したり、感情分析等も組み合わせたりして、さらなる分析にチャレンジしたいと思います。
また、今回用いた株価は365日毎日データがあるデータセットではなかったため、SARIMAモデルを用いた日別予測はできなかったのですが、毎日データがある気象データなどを使ってSARIMAモデルでの日別予測も試してみたいと思います。

Aidemyの受講期間はもうすぐ終了ですが、今後も学習を続けてスキルアップをしていきたいとおもいます。ここまで読んでくださりありがとうございました。

※このブログはAidemy Premiumのカリキュラムの一環で、受講修了条件を満たすために公開しています

初心者がAIモデルで株価予測してみた

目次