Groverのアルゴリズムで簡単なパズルを解く

量子アルゴリズムの一つである「Groverのアルゴリズム」について、「こう使えば良いのかな？」というのが割と固まったので、今後のためにある程度まとめておきます。
参考になる部分があれば幸いです。

実行環境

量子回路の実装にはqiskitを使用します。qiskitは、IBMQが提供しているpythonのライブラリです。
また、IBMQが提供しているIBM Q Experienceのアカウントを作成すると、クラウドを通じてqiskitやnumpyなど必要なライブラリをインストールせずに使用できるので、こちらを使う方がおすすめです。

IBM Q Experienceのアカウントは、普通の人か、研究機関に所属する研究者かどうかで使える実機の数が違うのですが、シミュレータで動かす場合は誰でも使えます。実機も7ビットまでは使えるっぽいです。

Groverのアルゴリズムとは1

量子探索アルゴリズムとも呼ばれています。理論的な解説は以下のサイトがとても分かりやすく、お世話になりました。

ただ、問題は「どう使うの？」って話なんです。Groverのアルゴリズムを調べると、皆さん理論面の解説は分かりやすいのですが、実装例がどれを見ても「0を探す」とか「1を探す」とかばかり。「0を探して0が見つかるのは当たり前じゃん」って話です。これだと、せっかく勉強したのに面白くないし、凄さもいまいち分からないですよね。
そこで、今回は簡単だけど「当たり前」ではないパズルを解いて、Groverのアルゴリズムの使い所について考えていきます。

パズル概要

正式名称はなさそうですが、以下のルールで「全てのボタンを点灯させる」ことがゴール、というパズルです。脱出ゲームのミニゲームにありそうな感じのやつですね。

1. ボタンを押すと、そのボタンと隣接したボタンの点滅が入れ替わる
2. 全てのボタンが光ったらゴール

3×3の場合、以下のようになります。

今回は3×3の問題を解いていきます。
その前にGroverのアルゴリズムの一般的な説明を挟みましょう。

Groverのアルゴリズムとは2

知っている方も多いと思いますが、Groverのアルゴリズムには、大きく分けると2つのシステムから成り立っています。

オラクル回路
オラクル(oracle)というのは、英語で「神託」という意味で、その名の通り、値$x$を入れると$x$が解であるかどうかを判定してくれる回路です。
もう少し数学的に書くと、オラクル回路の働きは以下のようになります。

O: \ket j =
\begin{cases}
    -\ket j & j\text{ が解のとき} \\
    \ket j & j\text{ が解でないとき} \\
\end{cases}

実際には、jという状態は2進数で構成されているわけなので、例えば4qubitなら、

\ket 0 =\ket{0000} =\ket0\otimes\ket0\otimes\ket0\otimes\ket 0 

だったり、

\ket 5 =\ket{0101} 

だったり、

\ket {14} =\ket{1110} 

というわけです。

振幅増幅回路
正式名称は分からないのですが、オラクル回路で位相が反転した（つまりマイナスになった）状態ベクトルの確率的な振幅を増幅させます。これをしないと、どれだけオラクル回路にかけても、正負だけ行ったり来たりしながら確率は変わらない（2乗したら正負の違いはなくなるから）わけです。
では、どうやって振幅を増幅させるのかというと、「一番最初の状態（つまり全状態ベクトルが均等に混ざっている状態）に対して折り返す」という操作をすれば良いわけです。
数式で書くと、n qubit, m=2^n 個の状態に対して、最初の状態を

\ket s =\frac{1}{\sqrt m}\sum_{j=0}^{m-1}\ket j

と書くと、振幅増幅回路は

U_s=2\ket s \bra s-I

と表せます。詳しい説明は上記のサイトを見た方が良いです。

オラクルをどう実装するか

ネット上の教材やブログ記事のほとんどは、理論の説明だけして、使い方の方は数字当てだけしてお茶を濁しています。これだと、「オラクル回路は簡単に組むのは難しくて、凄いアイディアが必要なのかも」と思ってしまいます。
ところが、オラクル回路というのは、「神託」という何ともエスパーな名前をしているのにも関わらず、実は最も単純で泥臭い回路なんです。

「探索問題」について考える
例えば、オフィスや大学などの大きな建物の警備員になったとします。あなたは、どこかの部屋の窓が一つだけ開いていて、その部屋を探しています。どうやって探しますか？
人によっては、「外からライトを当てて、反射しているかどうかで窓が開いているか分かる」など、頭の良い方法を思いつくかもしれません。では、誰でも思いつける、単純で泥臭い探し方は何でしょうか。それは「総当たりで全部屋探す」ことですよね。
あなたは、1階の101から順に窓が開いているかどうかを調べていきます。「扉の鍵を開け」、まず「正面の窓を確認」、次に「左右に窓があれば、それも確認」、そして「チェックリストに開閉のどちらかをチェック」というように、各部屋調べていきます。もしかしたら、「邪魔な椅子を退かす」「カーテンが閉じていたら一度開ける」みたいな場面もあるかもしれません。

決して頭の良いやり方ではありません。マニュアルに従った単なる繰り返し。n部屋あったらn回確認しないといけない、面倒な作業。
実はこのマニュアルが、Groverのアルゴリズムにおけるオラクルなのです。

パズルを解く

オラクルは「総当たり」の「マニュアル」である。では、今回のパズルの場合、「マニュアル」はどうなりますか？
それは、パズルのルールに既に示されています。

1. ボタンを押すと、そのボタンと隣接したボタンが点灯する
2. ボタンを押したあと、全てのボタンが光っていれば「正解」

つまり、「どのボタンを押すか」という入力状態が与えられれば、入力状態に1の操作をして、出力を2で判定すれば、与えられた入力状態が「正解」か分かるわけです。
そう考えると、自ずと「入力状態をどう表現するか」も決まります。9ビットの01で各ボタンを押すかどうかを表現できますね。入力状態は2^9=512通りです。
これをもとに、量子回路を組んでいきます。

ライブラリのインポート

IBM Q Experienceでの実装を想定していることに注意してください。

import numpy as np
import matplotlib.pyplot as plt

# Importing standard Qiskit libraries
from qiskit import QuantumCircuit, transpile, Aer, IBMQ, execute
from qiskit.tools.jupyter import *
from qiskit.visualization import *
from ibm_quantum_widgets import *
from qiskit.providers.aer import QasmSimulator
from qiskit.providers.ibmq.job import job_monitor
provider = IBMQ.load_account()

回路の概要

回路を実際に組む前に、大まかな回路の全容をまとめておきます。
今回使う量子ビット数は18です。入力状態は9ビットで済むのですが、その9ビットにゲートをかけて上書きしていくと入力状態を保持できなくなるので、

• ビット0〜8が入力状態を保持
• ビット9〜15に出力、正解を判定
• 逆操作で元の入力状態に戻し、振幅増幅回路をかける

を繰り返し、最後にビット0〜8を測定する、という流れになります。そのため古典ビットは9個です。
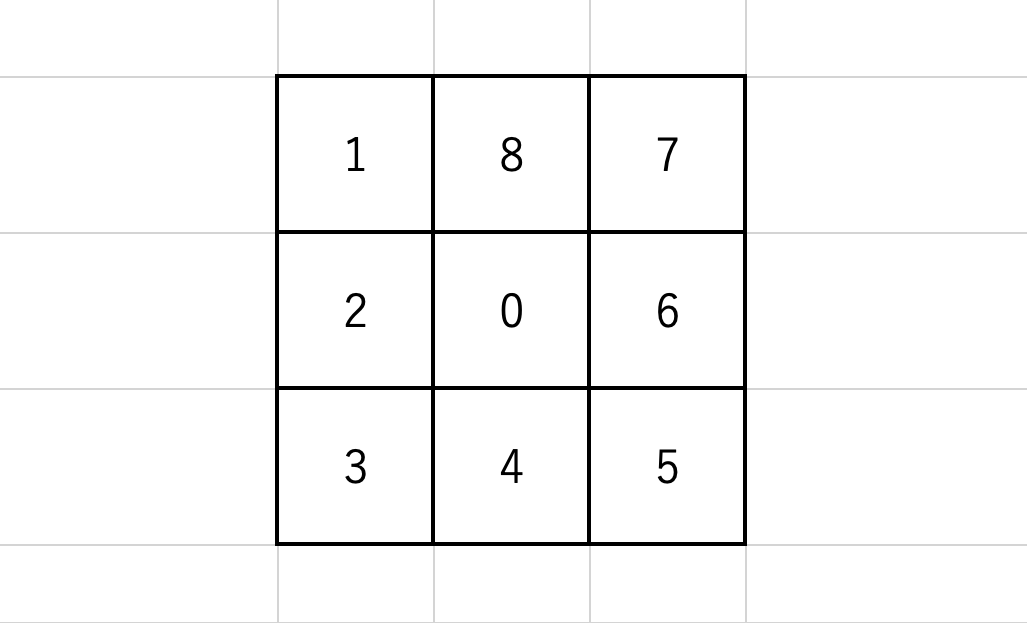
ボタンと量子ビットの番号は、以下のように対応付けておきます。出力状態の番号は入力+9と考えてください。

オラクル回路

まずは、ボタンを押す操作に対応する回路を組んでいきましょう。これは、「入力が1なら出力を反転させる」と言い換えることができるので、CNOTゲートで実装できます。例えば、ビット0が1なら、自身と隣接するボタンを点滅させるので、ビット0がコントロールビット、ビット9,11,13,15,17がターゲットビットです。

# ビット番号iを押す操作
def push_button(qc, i):
    if i == 0:
        qc.cx(0, 9)
        qc.cx(0, 11)
        qc.cx(0, 13)
        qc.cx(0, 15)
        qc.cx(0, 17)
    elif i == 1:
        qc.cx(1, 10)
        qc.cx(1, 17)
        qc.cx(1, 11)
    elif i == 8:
        qc.cx(8, 17)
        qc.cx(8, 16)
        qc.cx(8, 9)
        qc.cx(8, 10)
    elif i % 2 == 0:
        qc.cx(i, i+9)
        qc.cx(i, i+8)
        qc.cx(i, 9)
        qc.cx(i, i+10)
    else:
        qc.cx(i, i+9)
        qc.cx(i, i+8)
        qc.cx(i, i+10)

これらの操作で入力状態（ビット0〜8）は変化しないので、どの番号からかけても結果は変わりません。工夫は全くありませんが、「マニュアル」として最低限の要素を満たしているわけです。
次に、正解の状態だけ位相を反転させる回路を組んでいきます。

# 全ボタンが光っている時のみ位相を反転する
def is_correct(qc):
    qc.h(17)
    qc.mct(list(range(9,17)),17)
    qc.h(17)

「え、これだけ？」と思うかもしれませんが、qiskitに備え付けられているMCT = Multi-controlled Toffoli ゲートが超有能で、そのおかげで簡潔にまとまっています。MCTゲートは複数ビットを制御ビットにしてNOTをかけるゲートで、言うなればCNOTの上位互換です（実装方法によるコストの違いは無視しています）。
それに加えて、Xゲートの両側をHゲートで挟むとZゲートになることから、この回路全体は Multi-controlled Z ゲートになっています。つまり、回路を翻訳すると、
「ビット9〜16が全て1の場合のみ、ビット17の1の部分のみ位相を反転する」
＝「出力が全て1の時だけマイナスにする」
となります。

振幅増幅回路

次に、振幅増幅回路です。説明の前に回路を提示してしまいます。

# 正解の振幅を増幅する回路
def make_diffuser(qc, n):
    qc.h(range(n))
    qc.x(range(n))
    qc.h(n-1)
    qc.mct(list(range(n-1)),n-1)
    qc.h(n-1)
    qc.x(range(n))
    qc.h(range(n))

コードを見て分かることがありませんか？
実は、振幅増幅回路は何ビットでも同じ形で回路が組めるのです。その理由をもう少し見ていきましょう。
まず、回路の真ん中3列、H→MCT→Hは見覚えがありますよね。これはビットが111...の時だけマイナスをかける回路です。さらにその両側、全てのビットにNOTゲートをかけています。つまり、qc.h(range(n))で挟まれた部分は、ビットが000...のときだけマイナスをかける回路になっています。これは、以下のゲートと等しいです。

U = I - 2\ket 0 \bra 0 \ \ (\ket 0 = \ket{000\cdots})

では、このゲートを挟んでいる、全てのビットにHゲートをかける操作というのはどのような操作なのでしょうか？Hゲートは

H: \ \ket{0} \rightarrow \frac{\ket 0 + \ket 1}{\sqrt 2}

という、0と1を均等に混合するゲートでした。ということはn個のビットにそれぞれHゲートをかけたら、

H^{\otimes n}: \ \ket{000\cdots} \rightarrow \frac{1}{\sqrt{2^n}}\sum_{j=0}^{2^n-1}\ket j = \ket s

つまり、初期状態を作るゲートだったわけです。ということは、振幅増幅回路は

H^{\otimes n}(I - 2\ket 0 \bra 0 )H^{\otimes n} \newline
= H^{\otimes n}H^{\otimes n}-2(H^{\otimes n}\ket 0)(\bra 0 H^{\otimes n})
=I - 2\ket s\bra s

となり、理論で出てきた演算子と（マイナスにはなっていますが）一致します。

回路を完成させる

定義した関数を使って回路を完成させましょう。
早速コードを組んでいきます。

# 量子ビット数と古典ビット数
n = 9 #ボタンの数
q = 2 * n #量子ビット数. 2倍なのはボタン操作用に記録するビットがそれぞれあるから
c = 9 #古典ビット数

        
    
# 最初に全ての状態を同じ確率で重ね合わせる
circ_init = QuantumCircuit(q, c)
circ_init.h(range(n))



# オラクル回路
oracle = QuantumCircuit(q, c)
oracle.barrier()

# 各ボタンの操作を重ねる
for i in range(0, n):
    push_button(oracle, i)

oracle.barrier()

# 正解しているものだけ位相を反転させる
is_correct(oracle)

oracle.barrier()

# 逆操作で状態を元に戻す
for i in range(0, n):
    push_button(oracle, n-i-1)



# 振幅増幅回路
diffuser = QuantumCircuit(q, c)
diffuser.barrier()
make_diffuser(diffuser, n)


# 繋げてグローバーの繰り返し回路を作る
circ_g = oracle.compose(diffuser)

# 測定回路
meas = QuantumCircuit(q, c)
meas.barrier()
meas.measure(range(n),range(n))


# n回繰り返した回路を出力する
def repeated_circuit(n):
    circ = circ_init
    for i in range(0,n):
        circ = circ.compose(circ_g)
    circ = circ.compose(meas)
    return circ


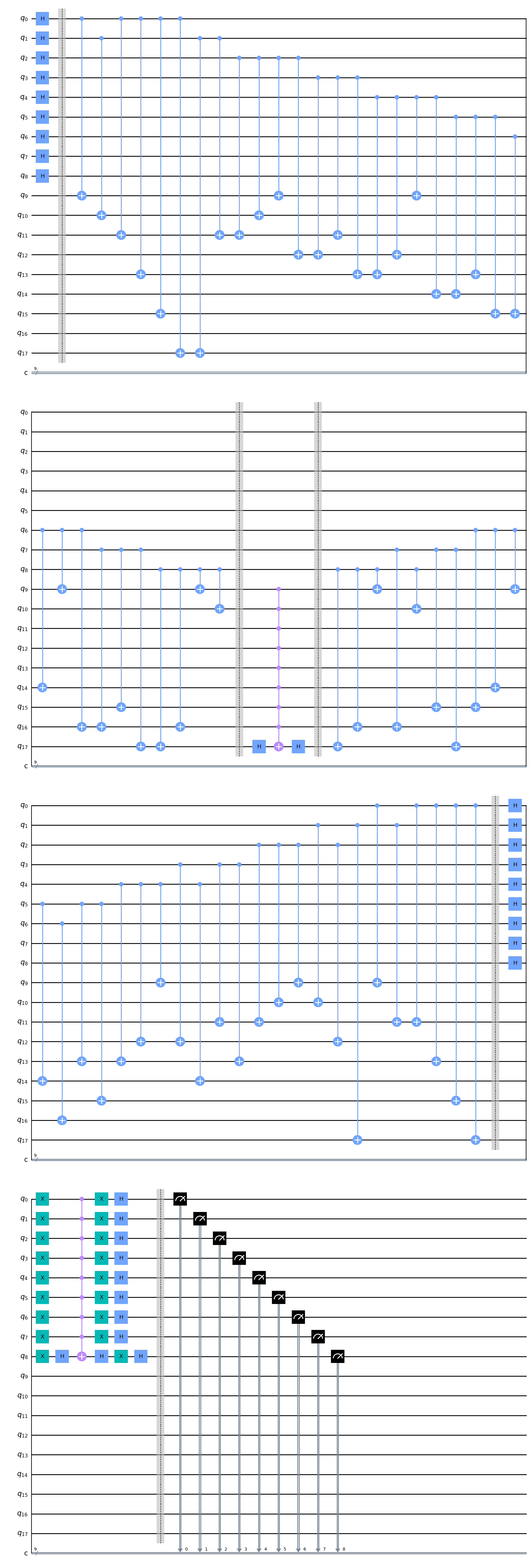
# 繰り返し回数が1の時の回路を表示
repeated_circuit(1).draw(output='mpl')

回路は次のようになります。結構長いですね。

回路をシュミレータで実行する

回路も完成したので、早速動かしてみましょう！...と言いたいところですが、最後に一つ考えるべきことがあります。それは、「回路を何回繰り返すか」という問題です。
「適切な繰り返し回数がある」という話は、さっきのリンクの解説が分かりやすいのでぜひ見て欲しいですが、回数自体は普通に数式で調べることができます。探索ビット数をn, 正解の個数をmとして、

y = \left(\frac{\pi}{2}+\pi x\right)\frac{1}{2\arcsin(m/\sqrt{2^n})}-\frac12

という式の、「整数値xに対するyに近い整数」が、繰り返し回数になるというわけです。yが整数に近いほど、正解の割合が大きくなっていきます。手計算で出すのは流石に面倒なので、グラフにして確認してみます。

9ビットの場合なので、繰り返し回数nは
解が1個の場合、n = 17
解が2個の場合、n = 8
解が3個の場合、n = 5 ...
が最適なようです。
（実は、シミュレータの場合、nがそれほど大きくなくても差が目に見えて分かるので、あまり気にする必要はない）

繰り返し回数も決まったので実行していきましょう。結果は、測定回数が多かった順に10個だけ表示するようにして、解がはっきり表れるか確認します。

#シミュレータで試す
simulator = Aer.get_backend('qasm_simulator')

shots = 8192 # 実行回数
n = 17 # 繰り返し回数

job_sim = execute(repeated_circuit(n), backend=simulator, shots=shots)

#実行結果から測定部分（辞書データ）のみ取得
counts_sim = job_sim.result().get_counts(repeated_circuit(n))

#得られた辞書データを大きい順にソート
sorted_counts_sim = sorted(counts_sim.items(), key=lambda x: x[1], reverse=True)[:10]
print(sorted_counts_sim)

実行例:

[('010101011', 8186), ('010110100', 1), ('110111000', 1), ('000101100', 1), ('001011100', 1), ('000011001', 1), ('101000110', 1)]

無事正解が求まりました！かなり高い確率で出せています。
ボタン操作と振幅増幅回路はそのままに、正解判定の部分だけ変えて色々試してみるのも良いかもしれません。

まとめ: 結局、アルゴリズムは役に立つの？

正解が求まってめでたしめでたし、と言いたいところですが、まだ肝心の問題が解決していません。それは、「どこが優れているのか」という問題です。
ただ、実はもうほとんど解決しています。
今回解いたパズルを例に考えてみましょう。入力状態の全パターンは512通りでした。総当たりで調べるなら、マニュアルを最大512回繰り返す可能性があります。平均だと256回ですね。
Groverのアルゴリズムの場合はどうでしょうか？マニュアルに対応しているのは繰り返し部分ですね。ということは、マニュアルを17回繰り返すだけで答えが確実に見つかります。
これがGroverのアルゴリズムの凄いところです。「完全にランダムな探索」という場面で、古典コンピューターではO(n)のオーダーで終えるものを、量子コンピューター
の場合、O(√n)で終えることができるわけです。（オーダーの導出については、上記のリンクを参考にしてください。）
もちろん、「完全にランダムな探索」というのがポイントです。ソートできた瞬間に一気に計算量が減りますし。ただ、古典的な「頭の良い」方法とは違うアプローチで計算量を減らせるのは楽しいですね。

最後に、Groverのアルゴリズムを実際の問題に適用するコツみたいなのを書いておきます。かなり抽象的ですが、

• 全ての入力状態を量子ビットに振り分けることができる
• 各出力状態に『正解』か『不正解』を一意に割り振ることができる
• 定められた操作や、制約条件に基づく状態変化がマニュアル化できる

この3つを満たせば、ある意味「実装できる」ことが確約されているのかなと思いました。その上で、どれだけコスト、ビット数を節約できるかというのも面白いところです。

以上、Groverのアルゴリズムで簡単なパズルを解く話でした。pythonも量子アルゴリズムも初心者なので、改善点たくさんあると思いますが、参考にしていただけたら幸いです。