今回、こちらを参考にg-hフィルタについて学んでいく。
これはRoger R. Labbe 著 Kalman and Bayesian Filters in Pythonです。
英語版は CC BY 4.0 International ライセンスで公開されています。
g-hフィルタとは
g-h フィルタとはあるデータの値をもつ時系列順のデータからそのデータの未来の値を予測するアルゴリズムである。
g と h はどちらもスケーリング係数を表す。
g は観測値に対するスケーリング係数であり、h は観測値の変化に対するスケーリング係数である。
g と h ではなく α と β が使われることもあり、そのときは α-β フィルタ と呼ばれる。
def g_h_filter(data, x0, dx, g, h, dt=1.):
"""
固定された g と h を使った g-h フィルタを単一の状態変数に対して適用する
'data': フィルタリングを行うデータ
'x0': 状態変数の初期値
'dx': 状態変数の変化率の初期値
'g': g-h フィルタの g 係数
'h': g-h フィルタの h 係数
'dt': タイムステップの間隔
"""
x_est = x0
results = []
for z in data:
# 予測ステップ
x_pred = x_est + (dx*dt)
dx = dx
# 更新ステップ
residual = z - x_pred
dx = dx + h * (residual) / dt
x_est = x_pred + g * residual
results.append(x_est)
return np.array(results)
(参考:https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python)
g-h フィルタは膨大な種類のフィルタの土台になっている(カルマンフィルタ、最小二乗フィルタ、ベネディクト-ボードナーフィルタなど)。
これらのフィルタは g と h に異なる方法で値を割り当てるものの、その点を除けばアルゴリズムは変わらない。
例えばベネディクト-ボードナーフィルタは g と h に特定の範囲に収まる定数を割り当てる。またカルマンフィルタのように g と h を各ステップで変化させるフィルタも存在する。
直感的な考え方
g-h フィルタの考え方の前にまずは真の値の推定においての直感的な考え方として体重計を例にとる。
同じ正確さの体重計2つを使用
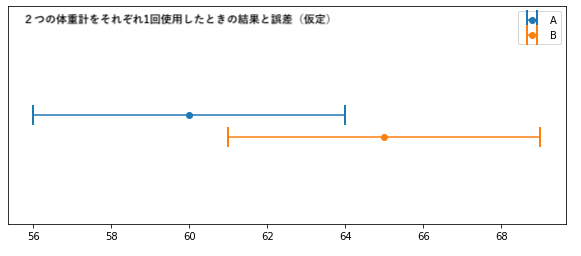
例えば、ほぼ同じ正確さ(誤差が同じ)と仮定した2つの体重計があったときにそれぞれの体重計で体重を測った。
体重計Aでは「60kg」、体重計Bでは「65kg」と2つともばらばらな値が観測された。
この場合どちらの体重計が正確かわからない。
体重計が二つとも正確でないなら、そして体重計で真の値より大きい値が観測される確率と真の値より小さい値が観測される確率が同じなら、真の値は A と B の間にあることが多いはずだ。
そのため多くの人の場合は、自分の体重の推定値を採用するときその二つの値の範囲の間にあると推定するはずである。(体重Aの方が軽いのでそちらを信じて採用する人もいると思うが)
この考え方は数学の期待値の考え方である。
もし、この計測を百万回行なったとしたとき”普通”ならなにが起こるだろうか?
もちろん、真の体重の値よりも2つの体重計は大きい値や小さい値を取りうることはあるだろうがほとんどの場合、真の値をまたぐことになるだろう。
たとえ、またがなかったとしてもAとBの間を選ぶことで悪い方の観測値の影響を和らげることができるためどちらか片方選んで誤差が大きくなるよりは優れた推定値が得られるはずである。
サンプルコード
import matplotlib.pyplot as plt
plt.errorbar(x=60, y=0, xerr=4, fmt='o', capthick=2, capsize=10, label="A")
plt.errorbar(x=65, y=0.2, xerr=4, fmt='o', capthick=2, capsize=10, label="B")
plt.ylim(1, -1)
plt.legend()
plt.gca().axes.yaxis.set_ticks([])
plt.show()
(参考:https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python)
異なる精度の体重計を使う
次に今までの体重計よりもより正確(誤差が少ない)な体重計(C)を使用した場合を考える。
先程の体重計Aよりも正確なため体重計Bを無視してAだけを使って推定値を得れば良いか。
この答えは2つの体重計を使うことにより「さらに正確になる」である。
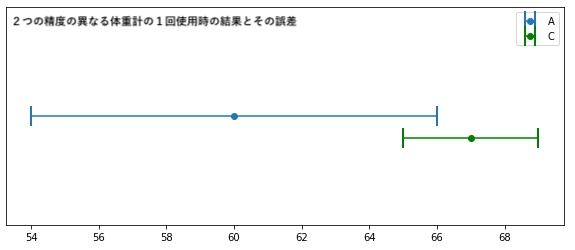
2つの体重計(A,C)の観測点がそれぞれ60kg、67kgとする。
Aの誤差が±6kg、Cの誤差が±2kgとすると以下のようなグラフになる。
サンプルコード
import matplotlib.pyplot as plt
plt.errorbar(x=60, y=0, xerr=6, fmt='o', capthick=2, capsize=10, label="A")
plt.errorbar(x=67, y=0.2, xerr=2, fmt='o', capthick=2, capsize=10, label="C", ecolor='green', mec='green', mfc='green')
plt.ylim(1, -1)
plt.legend()
plt.gca().axes.yaxis.set_ticks([])
plt.show()
(参考:https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python)
上のグラフからAとCのエラーバーの交わるところのどこかに真の値は存在であろう。
また、今回の注目すべき部分は重なっている部分に今回の観測値の60kg、67kgのどちらも含まれないことである。
つまり、Cの方が正確だからと言ってAの観測値をそのまま推定値に使ったり、AとCの平均値である63.5kgを推定値と扱うと体重計の正確さ(誤差)に関する知識からこの2つの値はどちらも真の体重の値としてありえないものであり推定値は65kg〜66kgの間の値とすべきである。
このことから2つのセンサー(今回のケースだと体重計)があると、たとえ片方のセンサーがあまり正確でなくても、1つのセンサーより推定値は正確になることがわかる。
同じ体重計を使う
持っている体重計が1つでそれで何度も体重を測った場合について考える。
同じ体重計を使う場合は同じ正確さの体重計2つを使用する場合と同様にそれぞれの観測値の平均を取るべきであることは説明した。
では1つの体重計で体重を10,000回計測した場合どうなるか?
一回の測定で真の値より大きい値が観測される確率と真の値より小さい値が観測される確率は同じだと仮定しているので、観測値の平均値が真の値に非常に近くなるはずである。
import numpy as np
measurements = np.random.uniform(50, 70, size=10000)
mean = measurements.mean()
print(f'平均:{mean:.4f}')
# out: 平均:59.9810
(参考:https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python)
ここでこの体重計の仮定として置いている
”真の値より大きい値が観測される確率と真の値より小さい値が観測される確率は同じ”
について考える。
これはつまり、真の値が60kgであったときに体重計は50kgとなる確率と70kgになる確率が等しいと仮定しているということである。
しかし、現実の体重計でこのことがあり得るだろうか?
現実のセンサーは真の値に近い値を観測する確率が高く、真の値から遠い値を観測する確率は真の値からの距離が大きくなるに従って小さくなるはずだ。
つまり、体重計のとりうる値は正規分布にしたがって真の値の近辺を観測しやすいと考えると
import numpy as np
mean = np.random.normal(60, 10, size=10000).mean()
print(f'観測値の平均は {mean:.4f}')
# out: 平均: 59.9226
(参考:https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python)
こちらも60に非常に近い。
ただこの方法は何度も体重を測る必要があるため真の値を表す推定値として現実的ではない。
体重を10日間計測する
ある体重計を使って毎日体重を測定したところ、59, 60, 59, 61, 60, 61, 59, 60, 59, 60 という観測値が得られたとしよう。
直感的にどう思うか?
「毎日1kgずつ体重が増えていて、ノイズ(誤差)により同じような体重が観測されてた」可能性もあれば、「毎日1kgずつ体重が減っていて、ノイズ(誤差)によって同じような体重が観測された」可能性もありうる。
しかし、そういった可能性が高いとは思えない。
コインを投げて10回連続で表が出る確率を考えれば、これは非常に低い。
この観測値だけでは確かなことは証明できないが、体重はほとんど変わらなかった可能性が非常に高く思える。
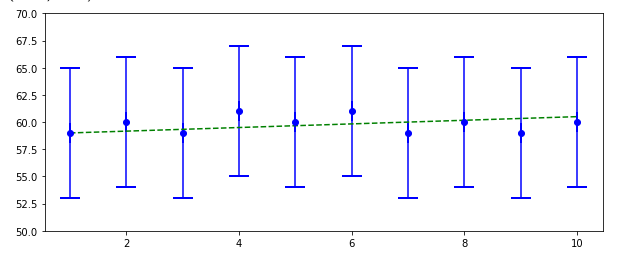
次のグラフは今回の体重の観測値+誤差をつけたエラーバーと緑の波線はあり得そうに見える真の体重(つまり観測値で説明できる理にかなった推定値)を表す。
サンプルコード
import matplotlib.pyplot as plt
plt.errorbar(range(1, 11), [59, 60, 59, 61, 60, 61, 59, 60, 59, 60],
xerr=0, yerr=6, fmt='bo', capthick=2, capsize=10)
plt.plot([1, 10], [59, 60.5], color='g', ls='--')
plt.ylim(50, 70)
次に別パターンでのシナリオを考える。
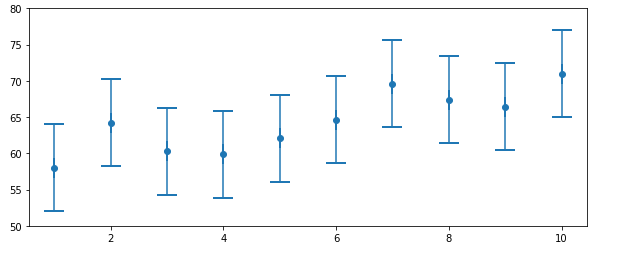
観測値が58.0, 64.2, 60.3, 59.9, 62.1, 64.6, 69.6, 67.4, 66.4, 71.0だった場合のグラフから何かわからないか考えよう。
サンプルコード
plt.errorbar(range(1, 11), [58.0, 64.2, 60.3, 59.9, 62.1, 64.6, 69.6, 67.4, 66.4, 71.0],
xerr=0, yerr=6, fmt='o', capthick=2, capsize=10)
plt.ylim(50, 80)
(参考:https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python)
このグラフの観測値から見ると明らかに体重は増加傾向にみえる。
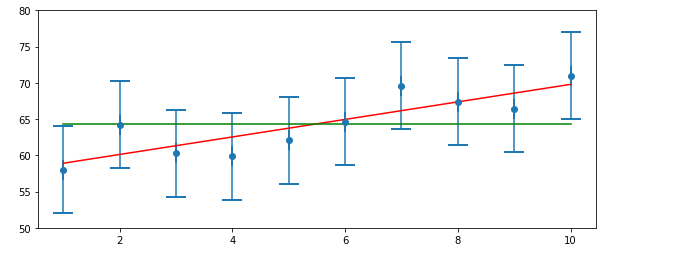
実際にこのグラフに体重が変わっていない仮説(緑線)と体重が増加する仮説(赤線)をグラフに表してみる。
そうすると可能性としてはやはり「体重が増加した」可能性が高そうだ。
これからわかるように観測値からでも体重の予想はある程度たてられることがわかる。
サンプルコード
plt.errorbar(range(1, 11), [58.0, 64.2, 60.3, 59.9, 62.1, 64.6, 69.6, 67.4, 66.4, 71.0],xerr=0, yerr=6, fmt='o', capthick=2, capsize=10)
ave = np.sum([58.0, 64.2, 60.3, 59.9, 62.1, 64.6, 69.6, 67.4, 66.4, 71.0]) / len([58.0, 64.2, 60.3, 59.9, 62.1, 64.6, 69.6, 67.4, 66.4, 71.0])
xs = range(1, len([58.0, 64.2, 60.3, 59.9, 62.1, 64.6, 69.6, 67.4, 66.4, 71.0])+1)
line = np.poly1d(np.polyfit(xs, [58.0, 64.2, 60.3, 59.9, 62.1, 64.6, 69.6, 67.4, 66.4, 71.0], 1))
plt.plot (xs, line(xs), c='r', label='hypothesis')
plt.plot([1, 10], [ave,ave], c='g', label='hypothesis')
plt.ylim(50, 80)
(参考:https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python)
体重の予測を行う
一日に約1kg体重を増すと知っている状況を仮定する。
初日の観測値は58kgだとする。最初は何も情報がないためこの値を推定値とする。
次の日の体重はいくつになると予想できるか?
一日に約1kg体重が増えると仮定しているため次の日の体重は59kgと予想できる。
さてこの予測がどれほど正しいだろうか?
もちろん、「一日に約1kg体重が増える」のが全体に正しいと決め込んで10日間の予測値を計算することもできるが、体重計を使っておいてその観測値を捨てるのは馬鹿な真似に思える。
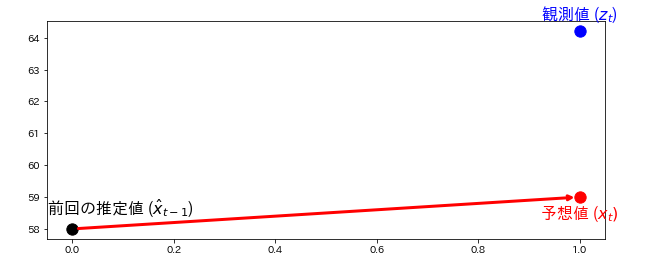
そこで観測値も見てみる。次の日に体重に乗ると64.2kgを指した。
(参考:https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python)
このグラフからわかるように予測値と観測値が合っていない。
しかし、これは驚くようなことでもないはずだ。予測値が必ず観測値と一致するなら、観測値がフィルタに新しい情報を追加することはない。
ではどうするか?
観測値だけから推定値を計算すると、予測値が結果に影響せず
予測値から推定値を計算すると観測値が無視されてしまう。
つまり、2つの値を活用するには予測値と観測値を何らかの方法で混ぜ合わせる必要がある
この2つの値を混ぜ合わせるーこれは前に触れた体重計2つを使用する状況とよく似ている。
そのときの結果によれば予測値と観測値の間にある値を推定値として選ぶことは良い選択だと言える。
では、予測値と観測値の間のどの位置を推定値とすべきだろうか?
今回の場合、体重計の正確さと予測値の正確さはことなり一般的に観測値よりも予測値の方がある程度正確であることが多いように思える。(一日で前回の推定値から6kgも増えるだろうか?)
そのため、前に触れた精度の異なる体重計の結果から推定値は観測値よりも予想値に近い値を取るべきだと言える。
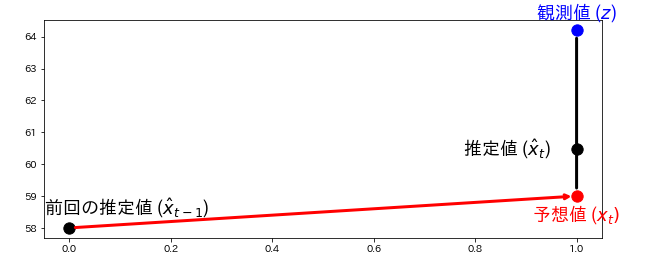
この考え方をグラフに示す。
サンプルコード
plt.annotate('', xy=[1,59], xytext=[0,58],arrowprops=dict(arrowstyle='->',ec='r', lw=3, shrinkA=6, shrinkB=5))
plt.annotate('', xy=[1,59], xytext=[1,64.2],arrowprops=dict(arrowstyle='-',ec='k', lw=3, shrinkA=8, shrinkB=8))
est_y = (58 + .4*(64.2-58))
plt.scatter ([0,1], [58.0,est_y], c='k',s=128)
plt.scatter ([1], [64.2], c='b',s=128)
plt.scatter ([1], [59], c='r', s=128)
plt.text (1.0, 58.8, "予想値 ($x_t)$", ha='center',va='top',fontsize=18,color='red')
plt.text (1.0, 64.4, "観測値 ($z$)",ha='center',va='bottom',fontsize=18,color='blue')
plt.text (-0.05, 59.0, "前回の推定値 ($\hat{x}_{t-1}$)", ha='left', va='top',fontsize=18)
plt.text (0.95, est_y, "推定値 ($\hat{x}_{t}$)", ha='right', va='center',fontsize=18)
(参考:https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python)
推定値をスケールする係数を適当に選ぶ。
「観測値より予測値の方がある程度精度がよい」という信念のもと推定値の式は以下で計算することにする。
推定値 = 予測値 + \frac{4}{10}(観測値-予測値)
ここで観測値と予測値の違いは残差(residual)と呼ばれる。
上述した推定値の算出方法(g:推定値をスケールする係数)を適用したとき今回の観測結果に対してどのような結果になるかコードとその結果のグラフを示す。
また、今回もう1つ定めなければならない係数(h:観測値の変化に対するスケーリング係数)については単位は「重さ/時間」なので1日を時間ステップとしている。
※今回、仮定として一日あたりの体重増加は1kgと仮定する。
今回、真の体重データはスタート時の体重を60kg。
体重の増加は1日あたり1kgになるように作成しました。
つまり、初日(0日目)の真の体重は60kg,二日目(1日目 、軽量初日)の真の体重は61kgとなります。
なお、初日の体重の初期値は60kgと設定する。
# 10日間分の体重計の観測値
weights = [58.0, 64.2, 60.3, 59.9, 62.1, 64.6,
69.6, 67.4, 66.4, 71.0, 71.2, 72.6]
def predict_using_gain_guess(estimated_weight, gain_rate):
# フィルタ結果の格納場所
estimates, predictions = [estimated_weight], []
time_step = 1.0 # day
scale_factor = 4.0/10
# フィルタリングの文献では観測値に z を使うことが多い
for z in weights:
# 前回の推定値から予測値の算出
predicted_weight = estimated_weight + gain_rate * time_step
# フィルタ更新部分
estimated_weight = predicted_weight + scale_factor * (z - predicted_weight)
# 結果の格納
estimates.append(estimated_weight)
predictions.append(predicted_weight)
return estimates, predictions
#初期値の設定
initial_estimate = 60
estimates, predictions = predict_using_gain_guess(
estimated_weight=initial_estimate, gain_rate=1)
xs = [i + 1 for i in range(len(weights))]
plt.plot(range(0, 13), estimates, c='b', label='推定値', marker='o')
plt.plot([0, 12], [60, 72], c='k', label='真の体重')
plt.plot(range(1, 13), weights, c='black', label='観測値', marker='o', linestyle='', mfc='None', mec='black', mew=2)
plt.plot(xs, predictions, c='r', label='予測値', marker='v', linestyle=':')
plt.legend()
(参考:https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python)
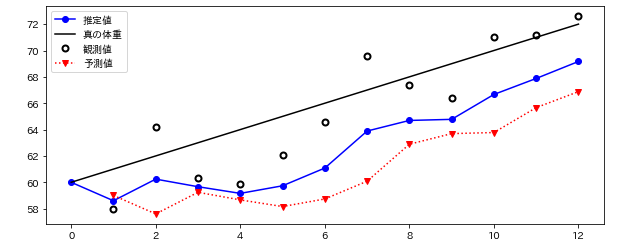
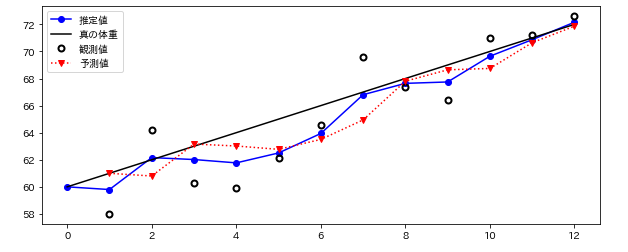
この結果から推定値は真の体重にかなりフィットしているように見える。
まず、青い実線はフィルタからが出力する推定値を表し初期推定値は60kgとしている。
赤い波線は予測値であり前回の推定値から計算した予測値を表す。体重の増加は一日1kgと仮定しているため第1日目では前日の推定値60kg(初期値)から61kgとなっている。
黒い実線は真の体重の増分を示す。
ここで確認するのは推定値は必ず観測値と予測値の中間にあることである。
計算される推定値を結んでも直線にはならないが、観測値を結んだものよりは振れ幅が小さく、観測値を生成するのに使った値に近くなっている。また時間が進むにつれ推測値が正確になっているようにも見える。
ただ、この結果はふざけたものである。
もともと体重の増分を一日1kg増加すると真の体重の増加推移と同じ仮定しているため結果が正しくなるのはとうぜんな結果である。
では先程の関数に体重の増減分を一日1kg減少すると推測するとどうなるか
サンプルコード
#初期値の設定
initial_estimate = 60
estimates, predictions = predict_using_gain_guess(
estimated_weight=initial_estimate, gain_rate=-1)
xs = [i + 1 for i in range(len(weights))]
plt.plot(range(0, 13), estimates, c='b', label='推定値', marker='o')
plt.plot([0, 12], [60, 72], c='k', label='真の体重')
plt.plot(range(1, 13), weights, c='black', label='観測値', marker='o', linestyle='', mfc='None', mec='black', mew=2)
plt.plot(xs, predictions, c='r', label='予測値', marker='v', linestyle=':')
plt.legend()
(参考:https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python)
これはあまり良い推定ができているとはいえない。
推定値は観測値からすぐに離れていっている。ここからわかることはデータの変化率を正しく推測しなければならないフィルタというのは明らかに役に立たない。
さらにたとえ最初の推測が正しかったとしても、その後の変化率が変わればフィルタは値の推定が失敗してしまうということになる。
ただここで注意してほしいのはフィルタはうまく適応できないが適応自体は起きている(調整が追いついていないだけ)ということである。
では、このフィルタを改善するために一日の体重増加率の初期推定値である1kgの代わりに
既存の観測値と推定値から計算するという方法がある。
1日目の予測値と2日目の観測値から体重の増加率を考えるとする。
2日目の体重の増加は1kgではなく4.4kgの体重増加を示しています(64.2-60.0=4.2のため)。
この情報を利用することは理にかなっています。
結局のところは体重の測定自体は体重の実測値に基づいているので有用な情報になります。
ノイズが含まれているかもしれませんが、ただ何の根拠もなく一日1kg増加(もしくは減少)すると推測するよりは優れた推測になるはずです。
では、新しい体重増加量/日を4.2kgにすべきでしょうか?
ちなみに前日の増加量は1kgです。せっかく2つの数値があるので今までのように2つの数値の中間の値を選んでみます。(今回は1/3[h:観測値の変化に対するスケーリング係数]にしてみます。)
ただ、今回のこの体重増加量は割合(1日あたりの増加量)のため単位を合わせるために以下のような式にします。
new gain = oldgain + \frac{1}{3}\frac{(観測値-予測値)}{1day}
weight = 60. # 体重初期値
gain_rate = -1.0 # 先程うまくいかなかった一日1kg減少すると仮定した増加率
time_step = 1.
weight_scale = 4./10
gain_scale = 1./3
estimates = [weight]
predictions = []
for z in weights:
# 予想ステップ
weight = weight + gain_rate*time_step
gain_rate = gain_rate
predictions.append(weight)
# 更新ステップ
residual = z - weight
gain_rate = gain_rate + gain_scale * (residual/time_step)
weight = weight + weight_scale * residual
estimates.append(weight)
plt.plot(range(0, 13), estimates, c='b', label='推定値', marker='o')
plt.plot([0, 12], [60, 72], c='k', label='真の体重')
plt.plot(range(1, 13), weights, c='black', label='観測値', marker='o', linestyle='', mfc='None', mec='black', mew=2)
plt.plot(xs, predictions, c='r', label='予測値', marker='v', linestyle=':')
plt.legend()
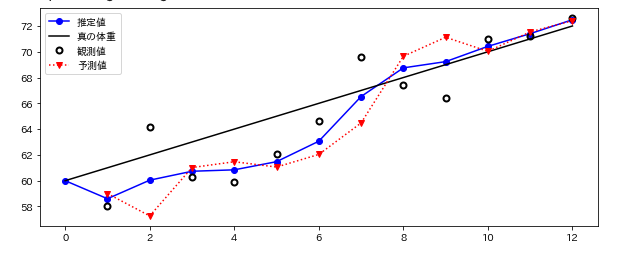
(参考:https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python)
このグラフはいい感じになっています。
最初の方では体重増加の推測が-1となっているためフィルターが正確に体重を予測するのに時間がかかってますが体重を正確に追跡できています。
g-hフィルタ
以上までがg-hフィルタと呼ばれているアルゴリズムのg と h の二つのスケーリング係数 (weight_scale と gain_scale) を表しています。
ここまでの要点で重要なことは以下のことです。
- 単一のデータ点を使うより複数のデータ点を使う方が正確なので、どんなに不正確であってもデータ点を捨てない。
- データ点が二つあるなら、必ずその中間にある値を推定値として選択して正確さを向上させる。
- 現在の推定値と変化率の推定から、次の観測値と変化率を予測する。
- 予測値と次の観測値をそれぞれの正確さでスケールして混ぜ合わせ、新しい推定値を計算する。
def g_h_filter(data, x0, dx, g, h, dt=1.):
"""
固定された g と h を使った g-h フィルタを単一の状態変数に対して適用する
'data': フィルタリングを行うデータ
'x0': 状態変数の初期値
'dx': 状態変数の変化率の初期値
'g': g-h フィルタの g 係数
'h': g-h フィルタの h 係数
'dt': タイムステップの間隔
"""
x_est = x0
results = []
for z in data:
# 予測ステップ
x_pred = x_est + (dx*dt)
dx = dx
# 更新ステップ
residual = z - x_pred
dx = dx + h * (residual) / dt
x_est = x_pred + g * residual
results.append(x_est)
return np.array(results)
(参考:https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python)
ここで最初に述べたg-hフィルタの関数を示す。
ここまでの流れから難しいところはないはずである。
体重問題に対するコードに含まれていた変数をすこし変化しただけで他の部分と変わっていないはずである。