$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$

量子テレポーテーション

今回は量子テレポーテーションを実装してみます。有名なアルゴリズムですが、数式ベースでも掘り下げてみたいと思います。

量子情報の専門書ではよく取り上げられていますが、共通して最初の方に書いてあると認識しています。つまり量子の特性を活かした基本的なアルゴリズムであります。

特にQKD(量子鍵配送)を理解するにあたり、量子テレポーテーションの考え方は通ずる話が多いと感じています。(時系列的にはテレポーテーションが後ですが)

量子テレポーテーションとは

端的にいうと以下のようになります。

Aさんが任意の量子状態$\ket{\psi}$を遠く離れたBさんに送るというものです。

自分が誤って認識していた点

"量子テレポーテーション"という名前だけ聞いたときの自分が考えていたのは量子状態が瞬時に遠距離に移動するというものですが、全然違いました。

①実際にAさんの量子は移動していない
②通信手段は古典通信

QKDの代表格、BB84も肝となるロジックは古典通信で行います。
感覚的には、ごちゃごちゃやったらBさん（受け手）の手元の量子がAさん（送り手）が用意したものになっているという感じ。

実際に流れを追ってみる

今回はアリスからボブへ、任意の量子状態を伝えたいと思います。
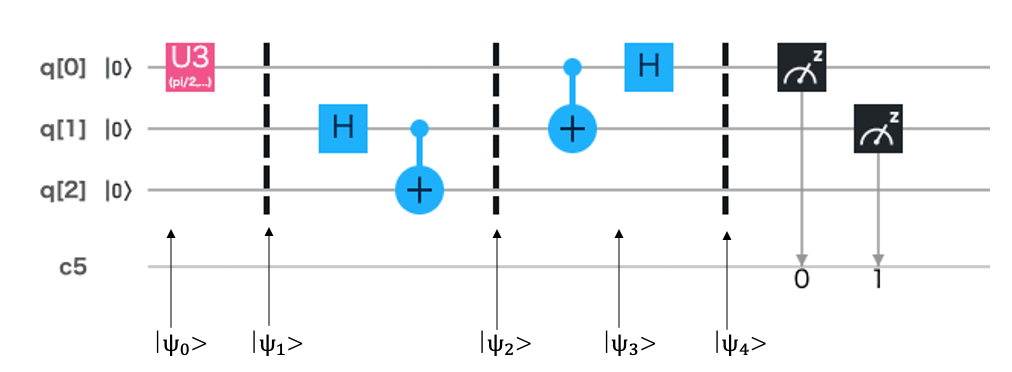
以下の量子回路で**アリスが持っているqubitはq[0]とq[1]、ボブが持っているのqubitはq[2]**です。

⓪初期状態は　

\ket{\psi_{0}}= \ket{0}_2⊗\ket{0}_1⊗\ket{0}_0 = \ket{000}_{210}

三つのqubitのうち、一番右のqubitが量子回路の一番上のqubit(q[0])に対応しています。つまり、q[0]が$\ket{0}_0$に対応します。
わかりにくくてすみません。

①アリスが送りたい量子状態を用意する。

\ket{\psi_{1}} = \ket{00}_{21}⊗(\alpha\ket{0} + \beta\ket{1})_0

$\ket{0}_0$をアリスが送りたい量子状態$(\alpha\ket{0} + \beta\ket{1})$にします。

②第三者イブがエンタングルしたペアq[1],q[2]ををそれぞれアリスとボブに配布

\ket{\psi_{2}} = \frac{1}{\sqrt{2}}(\ket{00}+\ket{11})_{21}⊗(\alpha\ket{0} + \beta\ket{1})_0

q[1],q[2]をエンタングルさせてアリスとボブに配布します。結果的にアリスはq[0],q[1]、ボブはq[2]を持っていることになります。
ここでイブが出てきましたが、ここのプロセスは人間ではなくプロトコルと考えた方がいいかもしれません。

ここまでで量子テレポーテーションの準備完了です！

③アリスの送りたいq[0]とイブから受け取ったもつれの片割れq[1]をもつれさせる

\ket{\psi_{3}} = \frac{1}{\sqrt{2}}( 
\alpha(\ket{00}+\ket{11})_{21}\ket{0}_0+\beta(\ket{01}+\ket{10})_{21}\ket{1}_0)

CNOTゲートなので$\beta$がかかっている方は、コントロールビットが1であるため

(\ket{00}+\ket{11})_{21}\ket{1}_0→(\ket{01}+\ket{10})_{21}\ket{1}_0

となっていることに注意します。(q[1]がフリップしています)

④q[0]にアダマールゲートをかける

\ket{\psi_{4}} = \frac{1}{\sqrt{2}}(\alpha(\ket{00}+\ket{11})_{21}\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})_0+\beta(\ket{01}+\ket{10})_{21}\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})_0)

= \frac{1}{2}(\alpha(\ket{00}+\ket{11})_{21}(\ket{0}+\ket{1})_0+\beta(\ket{01}+\ket{10})_{21}(\ket{0}+\ket{1})_0)

さらに展開して整理すると

= \frac{1}{2}((\alpha\ket{0}+\beta\ket{1})_{2}\ket{00}_{10}+(\alpha\ket{1}+\beta\ket{0})_{2}\ket{10}_{10}+(\alpha\ket{0}-\beta\ket{1})_{2}\ket{01}_{10}+(\alpha\ket{1}-\beta\ket{0})_{2}\ket{11}_{10})

ここでボブが持つq[2]が何やら最初にアリスが用意したqubitと似た形をしていることに気づきます。

⑤アリスの観測結果を古典通信でボブに伝える

アリスはq[0]とq[1]を持っているため、④で最終的に求めた式からアリスの観測結果は以下の4通りとなります。

\ket{00}_{10}, \ket{10}_{10}, \ket{01}_{10}, \ket{11}_{10}

⑥ボブは受け取った観測結果に応じてゲート操作を施す

さて、ここでボブは４通りの観測結果を得るため、観測結果によりボブのて手元のqubitをアリスが送りたい量子状態にするためには何かしらの操作を加えねばなりません。

以下に場合わけします。

( i )　$\ket{00}_{10}$だった場合

ボブの持つq[2]は$(\alpha\ket{0}+\beta\ket{1})_{2}$であるためそのまま

( ii )　$\ket{10}_{10}$だった場合

ボブの持つq[2]は$(\alpha\ket{1}+\beta\ket{0})_{2}$であるため、Xゲートを施すことにより

(\alpha\ket{1}+\beta\ket{0})_{2}→(\alpha\ket{0}+\beta\ket{1})_{2}

となります。

( iii )　$\ket{01}_{10}$だった場合

ボブの持つq[2]は$(\alpha\ket{0}-\beta\ket{1})_{2}$であるため、Zゲートを施すことにより

(\alpha\ket{0}-\beta\ket{1})_{2}→(\alpha\ket{0}+\beta\ket{1})_{2}

( iiii )　$\ket{11}_{10}$だった場合

ボブの持つq[2]は$(\alpha\ket{1}-\beta\ket{0})_{2}$であるため、Xゲート、Zゲート両方施すことにより

(\alpha\ket{1}-\beta\ket{0})_{2}→(\alpha\ket{0}+\beta\ket{1})_{2}

コードベースで追ってみる

⓪準備します

# Qiskitのライブラリをインポート
from qiskit import *
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np

# 3量子ビット回路を用意
qr = QuantumRegister(3)    
a_0 = ClassicalRegister(1)
a_1 = ClassicalRegister(1)
b_2 = ClassicalRegister(1)

qc = QuantumCircuit(qr,a_0,a_1,b_2)    

# 回路を描画
qc.draw(output="mpl")

下３列の回路は補助回路のようなものです。量子回路として扱うのは先ほど添付した図同様上の３列です。

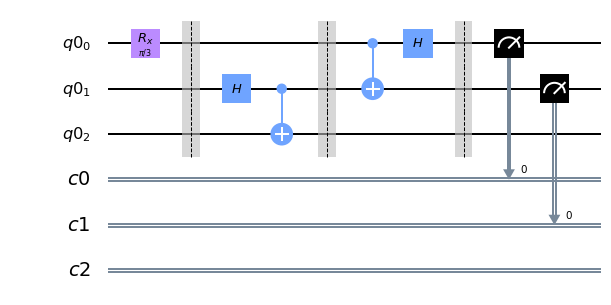
①アリスが送りたい量子状態を用意する。

# アリスのもつ未知の量子状態ψを今回はRxで作ります（図ではU3ゲートだが何でも良い、送りたい量子状態を作ってるだけ）
qc.rx(np.pi/3,0)
qc.barrier()

②第三者イブがエンタングルしたペアq[1],q[2]ををそれぞれアリスとボブに配布

# イブがEPRペアを作ってq[1]をアリスにq[2]をボブに渡します
qc.h(1)
qc.cx(1, 2)
qc.barrier()

③アリスの送りたいq[0]とイブから受け取ったもつれの片割れq[1]をもつれさせる

qc.cx(0, 1)

④q[0]にアダマールゲートをかける

qc.h(0)

⑤アリスの観測結果を古典通信でボブに伝える

qc.barrier()
qc.measure(0, a_0)
qc.measure(1, a_1)

# 回路を描画
qc.draw(output="mpl")

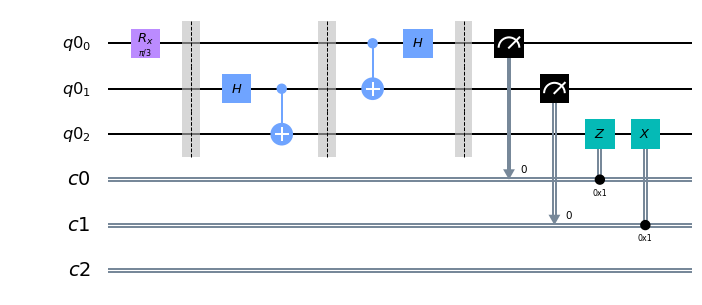
⑥ボブは受け取った観測結果に応じてゲート操作を施す

# q[0]が1ならZゲート、q[1]が1ならXゲートかける
qc.z(2).c_if(a_0, 1)
qc.x(2).c_if(a_1, 1)

qc.draw(output="mpl")

終わりに

どうでしょうか。量子テレポーテーションは何だか名前が抽象的なので、今回紹介したテレポーテーションの他にも色々種類があるかもしれません。

（QCQIには抽象化された回路の説明がありました）


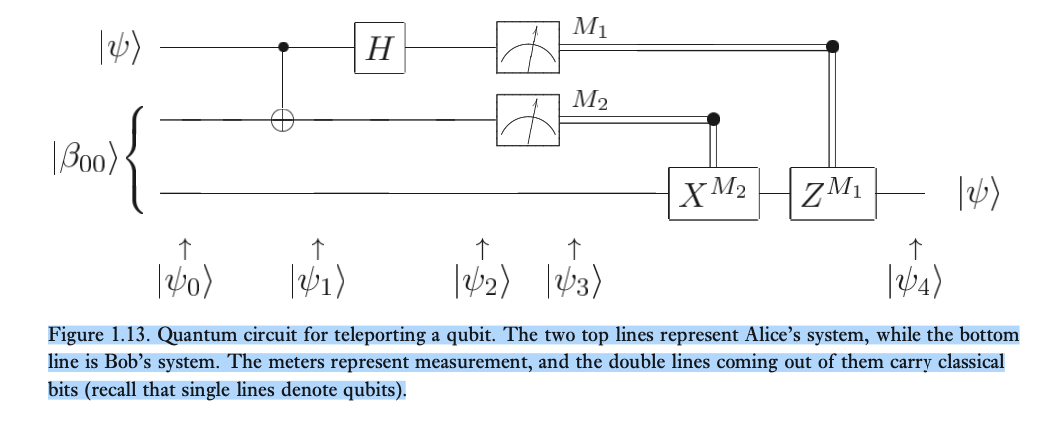
数式を追うのは大変ですが、いつの間にかボブの量子ビットがアリスが用意したものになってて感動します（笑）。
とにもかくにも、量子状態を直接古典通信で教えることなくボブに伝えることができました。この考え方はQKDでも重要になります。

参考文献

Quantum Computation and Quantum Information

日本のIBMの量子コンピュータチームの動画！このシリーズ貴重お世話になる予感。
https://youtu.be/YXho8MHC134