$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
量子インターネット(量子中継ネットワーク)の物理を量子鍵配送をスタート地点として説明していきたいと思います。
僕の整理のためでもあるので間違え等ありましたらご指摘お願いします。
量子鍵配送
まずはQKDです。とりあえずBB84に基づいて説明します。
①アリスがランダムなビット列と基底を選択
②ビット列を選択した基底で符号化し、ボブに送信
③ボブはアリスとは別でランダムな基底を選択し、受け取った光子をその基底で測定する
④各々の基底を共有し、基底が一致した部分のみを共有鍵とする。

1. 光子の発信 レーザーが代表的
理想的には1光子ずつ送りたいですが、現実はそうもいかず、光子数 $n$ が出力される確率は、平均光子数 $\mu$ として以下のようなポアソン分布に従います。
P(n)=
\frac{\mu^{n}}{n!}e^{-\mu}
このため複数光子が含まれていた場合、PNS攻撃が考えられますが、Decoy stateを使った手法(古典的な解析)で対処します。
2. 通信路 古典とは異なり、通信路で光子を増幅できません。
No-Cloning Theoremより
U(\left|\psi\right>\left|0\right>)=\left|\psi\right>\left|\psi\right>
のようなユニタリ操作は存在しないため、光子の情報を複製することができません。
そのため通信路の距離に応じて指数的に減衰してしまう光子をいかにして遠くまで飛ばすかというのが実験的・理論的に重要です。
3. 測定 光学素子による測定
ベーシックな考え方は以下のように偏光ビームスピリッタ(PBS)と検出器により測定します。

偏光によって空間的に分岐させ、どちらの検出器がクリックされたかによって受信者は送信者のビット情報を判断します。
ダークカウントレートをなるべく低いかつ安価なものを使用したいです。
注意点
任意のメッセージはQKD自体で送ることはできません。QKDで生成した共通鍵をOTPで使用します。
また、情報理論的安全性の文脈では送受信システムと、初期の認証は考慮しません。
情報理論的安全性(無条件安全性)は無限の計算能力を持つ計算機を仮定したときにも安全であるということで盗聴は難しいですが妨害する(鍵配送失敗させる)ことは可能です。
2ノード間の量子鍵配送ができましたが、より距離を長くしたいです。
どうすれば良いでしょうか?
とりあえずQKDプロトコルを接続してみましょう。
できました。これが量子鍵配送ネットワークだ!!
量子鍵配送ネットワーク
具体的な仕組みを見ていきます。
①各セグメントで量子通信と古典通信によりQKDを実行し、共通鍵を配布

ここで一番重要なのは、各ノードを信頼しなければならない点です。
以下のように悪意のあるノードがいた場合、秘密にすべき共通鍵が丸見えとなってしまいます。
ここまでの問題点として①単体のQKDでは光子の減衰により短距離②量子鍵配送ネットワークではTrusted node(古典中継)が前提のため、End-to-Endで情報理論的安全性が達成されません。
①②を量子物理的なアプローチで解決していくのが量子中継
量子中継ネットワーク
どのように解決していくのか、その前に量子中継に必要な道具を示していきます。
プロトコルの構造
量子中継を考えていく上で、セグメントのプロトコル(QKDプロトコルに該当)の構造は重要になってきます。ここでは量子中継的な文脈でプロトコルをカテゴライズします。
1. Sender receiver型

BB84、DPSとか
2. Meet in the middle型

MDI, Twin-fieldとか
3. Midpoint source型

BBM92とか
上記の1つのセグメントでのentanglement distribution rateの向上が量子中継ネットワーク全体のレート向上に繋がります。
線形光学ベル測定
線形光学ベル測定を用いたQKDプロトコル、MDI-QKDを用いて説明します。
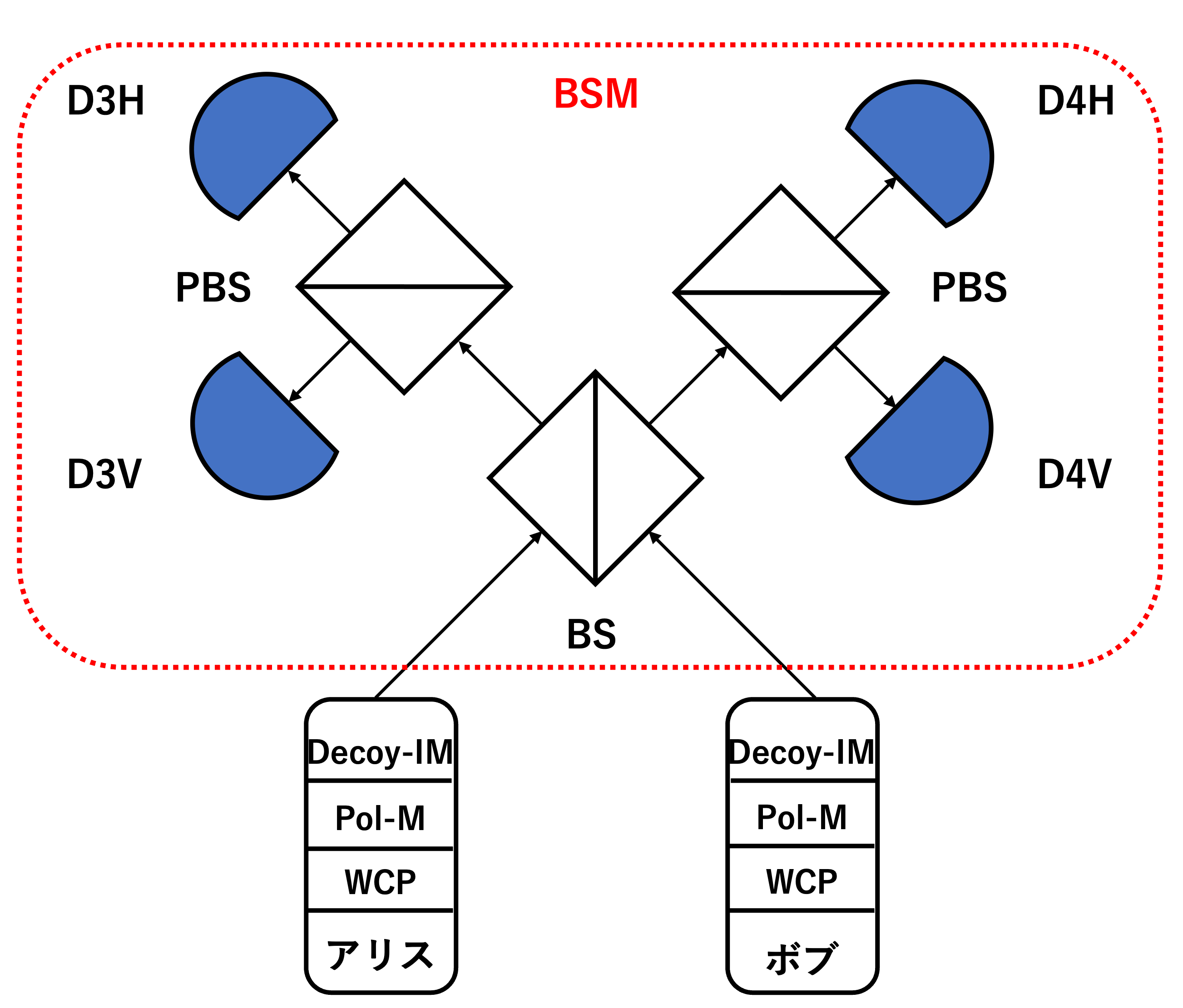
光学系は上記のような形になります。プロトコルの動きとしては、アリスとボブから発信された光子を中央でベル測定し、測定結果をアリスとボブに知らせることでビット情報を共有する流れです。赤色でBSMと示されている部分が線形光学ベル測定を行う部分です。
線形光学ベル測定は4つの検出器のクリックのされ方によってベル状態を見分ける手法です。アリスとボブがどのような入力を行なったときにどのようなベル状態として測定されるのかが重要です。
アリスとボブからの入力を$i_{1},i_{2}$として出力(ビームスピリッタ通過後)を$o_{3}, o_{4}$とすると、
\begin{pmatrix}
o_{3} \\
o_{4}
\end{pmatrix}
=
\frac{1}{\sqrt{2}}
\begin{pmatrix}
1 & i \\
i & 1
\end{pmatrix}
\begin{pmatrix}
i_{1} \\
i_{2}
\end{pmatrix} \\
\Leftrightarrow \begin{pmatrix}
i_{1} \\
i_{2}
\end{pmatrix}
=
\frac{1}{\sqrt{2}}
\begin{pmatrix}
1 & -i \\
-i & 1
\end{pmatrix}
\begin{pmatrix}
o_{3} \\
o_{4}
\end{pmatrix}
のようになります。これを用いて、各ベル状態がどのように検出器にクリックされるかみていきます。$1, 2$はBSへの入力位置を示し、$3, 4$はBSからの出力位置を示します。
パターン1 $\left|\psi^{-}\right>$のとき
\left|\psi^{-}\right>_{12}=\frac{1}{\sqrt{2}}(\hat{h}^{\dagger}_{1}\hat{v}^{\dagger}_{2}-\hat{v}^{\dagger}_{1}\hat{h}^{\dagger}_{2})\left|0, 0\right>_{1, 2} \\
\Rightarrow \frac{1}{\sqrt{2}}(\hat{h}^{\dagger}_{3}\hat{v}^{\dagger}_{4}-\hat{v}^{\dagger}_{3}\hat{h}^{\dagger}_{4})\left|0, 0\right>_{3, 4}
$H_{3}, V_{4} or V_{3}, H_{4}$で検出された時、つまり検出器D3HとD4V、またはD3VとD4Hで検出された時に$\left|\psi^{-}\right>$だと判断します。
パターン2 $\left|\psi^{+}\right>$のとき
\left|\psi^{+}\right>_{12}=\frac{1}{\sqrt{2}}(\hat{h}^{\dagger}_{1}\hat{v}^{\dagger}_{2}+\hat{v}^{\dagger}_{1}\hat{h}^{\dagger}_{2})\left|0, 0\right>_{1, 2} \\
\Rightarrow-\frac{i}{\sqrt{2}}(\hat{h}^{\dagger}_{3}\hat{v}^{\dagger}_{3}+
\hat{v}^{\dagger}_{4}\hat{h}^{\dagger}_{4})\left|0, 0\right>_{3, 4}
$H_{3}, V_{3} or V_{4}, H_{4}$で検出された時、つまり検出器D3HとD3V、またはD4VとD4Hで検出された時に$\left|\psi^{+}\right>$だと判断します。
パターン3 $\left|\phi^{\pm}\right>$のとき
\left|\phi^{\pm}\right>_{12}=\frac{1}{\sqrt{2}}(\hat{h}^{\dagger}_{1}\hat{h}^{\dagger}_{2}\pm\hat{v}^{\dagger}_{1}\hat{v}^{\dagger}_{2})\left|0, 0\right>_{1, 2} \\
\Rightarrow-\frac{i}{2}(\hat{h}^{\dagger}_{3}\hat{h}^{\dagger}_{3}+
\hat{h}^{\dagger}_{4}\hat{h}^{\dagger}_{4}\pm\hat{v}^{\dagger}_{3}\hat{v}^{\dagger}_{3}\pm\hat{v}^{\dagger}_{4}\hat{v}^{\dagger}_{4})\left|0, 0\right>_{3, 4}
2光子が$H_{3} or H_{4} or V_{3} or V_{4}$で検出された時、つまり検出器D3H、D3V、D4V、D4Hのいずれかで検出された時は$\left|\phi^{+}\right>$もしくは$\left|\phi^{-}\right>$のいずれかで判別できません。
以上から、$\left|\psi^{-}\right>, \left|\psi^{+}\right>, \left|\phi^{-}\right>, \left|\phi^{+}\right>$のうち二つのベル状態が判別可能ということになります。
つまり線形光学ベル測定では基本的に成功確率が50%です。
この線形光学ベル測定を用いてどのように鍵配送を行うのでしょうか。

MDI-QKDでは、中央にいるチャーリーさんがアリスとボブに測定結果を古典通信で伝えます。
測定結果というのは検出器がどのようにクリックされたかという内容です。
アリスとボブはパターン1,2であればベル測定が成功し、どの状態かわかります。パターン3の場合は失敗したんだなとわかります。
そしてアリスとボブはBB84同様基底情報を交換し、ビット情報を共有します。
例えば図のケースの場合、HV基底でアリスがH偏光、ボブがV偏光を発信し、ベル状態が$\left|\psi^{-}\right>$であったとします。アリスとボブはチャーリーから$\left|\psi^{-}\right>$であったことを知り、またアリスからしてみると
「自分はH偏光だったからボブはV偏光だったんだな」
ということがわかります。
しかし、チャーリーにとってはどうでしょうか。
測定結果が$\left|\psi^{+}\right>$であったことはわかりますが、アリスとボブが各々H偏光を送信したかV偏光を送信したかまではわかりません。

つまりチャーリーに悪意があった場合でも盗聴されることはありません。
この部分が重要です。
このロジックにより中継ノードを信頼できなくても、情報理論的安全性をもたらすことができます。
偏光状態でなくともDLCZのような一光子干渉の場合でも同様です。
Entanglement Swapping
ベル測定に関して学んだところで、今度はEntanglement Swapping(以下ES)に関して説明します。
①各のセグメントでもつれ光子対を共有

AB間、BC間の構造は上で記述されたうちのどれでもよいです。例えばDLCZであればMeet in the middle型。とにかく二者間でもつれ(Bell pair)を共有します。
AB間:\left|\psi^{-}\right>_{A0B0}=\frac{1}{\sqrt{2}}(\left|H\right>_{A0}\left|V\right>_{B0}-\left|V\right>_{A0}\left|H\right>_{B0}) \\
BC間:\left|\psi^{-}\right>_{B1C1}=\frac{1}{\sqrt{2}}(\left|H\right>_{B1}\left|V\right>_{C1}-\left|V\right>_{B1}\left|H\right>_{C1})
②Bは、Aともつれている光子B0とCともつれている光子B1でベル測定を行います。

\left|\psi^{-}\right>_{A0B0} \otimes \left|\psi^{-}\right>_{B1C1} \\
=\frac{1}{2}(\left|\psi^{-}\right>_{B0B1} \otimes \left|\psi^{-}\right>_{A0C1}+\left|\psi^{+}\right>_{B0B1} \otimes \left|\psi^{+}\right>_{A0C1} \\
+\left|\phi^{-}\right>_{B0B1} \otimes \left|\phi^{-}\right>_{A0C1}+\left|\phi^{+}\right>_{B0B1} \otimes \left|\phi^{+}\right>_{A0C1}) \\
上式よりBでベル測定を行うとAC間(A0C1間)でのもつれは、
\left|\psi^{-}\right>_{A0C1}, \left|\psi^{+}\right>_{A0C1}, \left|\phi^{-}\right>_{A0C1}, \left|\phi^{+}\right>_{A0C1}
のいずれかに確定し、結果的に二つのエンタングルメントを消費し、拡張したエンタングルメントを作成しました。これは量子性を維持したまま中継しており、Bを信頼せずとも成立する情報理論的安全性を維持していると言えます。
ESが完了した後は測定すればQKDが実行できますし、双方量子コンピュータと接続すれば分散量子計算が実行できるなど、実行可能なアプリケーションの幅が広がります。
しかし、量子中継を用いて長距離化を行いたい場合、ESだけでは十分条件にはなりません。
量子メモリ
量子メモリは量子インターネット(量子中継ネットワーク)において重要な役割を果たします。
ここでは量子メモリの物理には触れず、十分な時間保存できる機構と定義します。
例えば上記のように各セグメントでエンタングルメントを配布するような状況を考えます。AC間の距離がLだとすると、光子は距離Lの減衰に耐えなければなりません。
ですが、量子メモリが各ノードに設置されているとどうでしょうか。
光子が受ける減衰は距離L/2の減衰になります。
これは例えばAB間ではもつれ配布が成功し、BC間で失敗した場合に、量子メモリがない場合は再度各セグメントでもつれ配布を実行し直さなければなりません。ですが量子メモリがある場合、成功したセグメントに関しては他のセグメントが成功するまで量子メモリで量子情報を保存しておくことができます。
このようにして、量子メモリの存在が量子中継ネットワークの減衰の傾きを小さくすることができます。
※ 量子メモリを使用せずに量子中継を行うアプローチとして全光量子中継があります。
entanglement purification
さらに改善していきたいといった場合にどんなアプローチが考えられるでしょうか。
エンタングルメントとして今回はBell状態で説明しましたが、もつれ配布を行う時、フィデリティを維持したまま配布するというのは難しく、
\rho_{ab} = F\left|\phi^{+}\right>_{ab}\bra{\phi^{+}}+(1-F)\left|\psi^{+}\right>_{ab}\bra{\psi^{+}}
のような混合状態になってしまいます。このような状態を複数消費していって、最大エンタングルメント状態であるBell状態に近づけようというのがお気持ちになります。
例えば以下のように光学系でpurificationすることを考えます。

このプロトコルの場合は、4つのoutput(4 mode case)にそれぞれ1光子ずつ出力された場合を選択し、purificationを行います。ただし4 mode caseにならない場合があり、
\left|\phi^{+}\right>_{a1b1}\left|\psi^{+}\right>_{a2b2}, \left|\psi^{+}\right>_{a1b1}\left|\phi^{+}\right>_{a2b2}
このようなケースの場合は捨てます。
一方、
\left|\phi^{+}\right>_{a1b1}\left|\phi^{+}\right>_{a2b2}, \left|\psi^{+}\right>_{a1b1}\left|\psi^{+}\right>_{a2b2}
の場合、purificationを行うことにより、
\left|\phi^{+}\right>_{a3b3},\left|\psi^{+}\right>_{a3b3}
をそれぞれ $F^2/2, (1-F)^2/2$で得ることができ、
\rho^{\prime}_{ab} = F^{\prime}\left|\phi^{+}\right>_{ab}\bra{\phi^{+}}+(1-F^{\prime})\left|\psi^{+}\right>_{ab}\bra{\psi^{+}} (F^{\prime}=\frac{F^2}{F^2+(1-F)^2})
を得ることができ、$F^{\prime}$は$F$が0.5より大きい時、$F^{\prime}>F$となります。さらにこの処理を繰り返すことにより、最大エンタングルメントに近づけることができ、ES等を行いやすくできます。
最後に
今回は光学的なところを中心にQKDから量子インターネットに必要な物理を紹介しましたが、量子メモリなど掘り下げていくと様々な物理系が登場してきます。
また、量子インターネットの物理を考えましたが、量子インターネットを考える上ではより上のレイヤーも考えなければいけません。
参考文献
[1]Bennett, C. H. & Brassard, G. in Proc. IEEE Int. Conf. on Computers, Systems and Signal Processing 175–179 (IEEE, New York, 1984).
[2]Measurement-Device-Independent Quantum Key Distribution Hoi-Kwong Lo, Marcos Curty, and Bing Qi Phys. Rev. Lett. 108, 130503 – Published 30 March 2012
[3]量子インターネットタスクフォース ホワイトペーパー https://qitf.org/files/20210210_qitf_whitepaper.pdf
[4]Pan, JW., Simon, C., Brukner, Č. et al. Entanglement purification for quantum communication. Nature 410, 1067–1070 (2001). https://doi.org/10.1038/35074041
[5]Vasileios Mavroeidis, Kamer Vishi, Mateusz Dominik Zych, Audun Jøsang. The Impact of Quantum Computing on Present Cryptography. DOI: 10.14569/IJACSA.2018.090354 Article Published in International Journal of Advanced Computer Science and Applications(ijacsa), Volume 9 Issue 3, 2018.





