1. はじめに
当社は、複雑なデータにも対応可能で、かつ説明性の高いホワイトボックス型AI、EXAMHEL1(特許登録済)を開発しました。EXAMHELは、進化型自己組織化マップ(ESOM)の一種です。自己組織化マップとは、教師なし学習の1手法で、分類のルールを教えていないにも関わらず、データを与えると、データの特性を反映したマップを生成します。
自己組織化マップの学習ステップは、人間が言葉を覚える過程に似ていると言われています。赤ちゃんが言葉を覚える時は、まだ言葉が分からないので、教えることができません。赤ちゃんは、人間が話す言葉を聞き、自然と単語を分類し、場面に応じて言葉を使うことを覚えていきます。
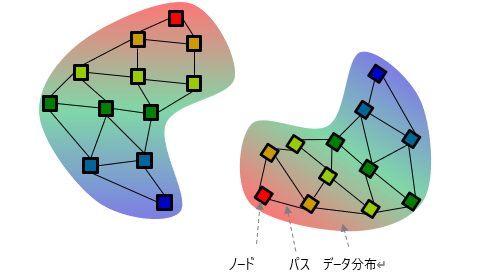
進化型自己組織化マップでは、データの集合をノード(代表点)の集合で近似し、つながりのあるノード間をパスで接続して自己組織化マップを作成します。非線形なデータ分布に対しても柔軟なクラスタリングが可能な特徴を持ちますが、学習時に設定するハイパーパラメータに敏感で学習が不安定になる欠点があります。EXAMHELでは、ハイパーパラメータを見直し、パスとノードに年齢の概念を導入し、活性度=活性値/年齢が閾値以下のノードとパスを削除することで、安定したオンライン学習を実現しています。本稿では、EXAMHELが学習した自己組織化マップのことをEXAMHELマップと呼びます。
EXAMHELは以下のような特徴を持っています。
- 少ないパラメータで安定したオンライン学習が可能 です。
- 非線形なクラスタリングにも対応し、クラスタ数を指定する必要がありません。
- 教師なし学習の一種ですが、教師あり学習にも適用可能です。
- 小数の教師データで、汎化性能が高い非線形な学習モデルを得ることができます(一般的には少数データに対して非線形な学習を行うと、汎化性能が落ちる傾向があります)。
- データとノードの位置関係で決まるため、結果の説明性を有しています。
2. EXAMHELのアルゴリズム
EXAMHELはオンライン学習でマップを生成していきます。最初のデータが初期ノードとなり、2番目以降のデータについては、最も近いノードとの距離$d_1$が閾値$d_{max}$以下であれば、ノードに属するデータと判断し、近接ノードの情報を更新します。一方、$d_1$が閾値$d_{max}$よりも大きければ、そのデータを新規ノードとして登録します。このようなシンプルなステップで学習マップを作成していきます。
より詳細なEXAMHELのアルゴリズムを以下に示します。なお、本記事の内容は、詳細なアルゴリズムを把握しなくても理解できますので、以下に説明するアルゴリズムについては、ご興味のある方のみお読みいただき、それ以外の方は、「3. EXAMHELを利用した教師なし学習」にお進みください。
① ハイパーパラメータの決定:入力データ$D(i)$ ($i=1~M$)を分析し、パラメータと初期ノードを設定します。
② データインデックス$i=1$とします。
③ $D(i)$に近いノードを、距離が近い順に第$N$勝者(距離$d_n$)まで求めます。
④ $d_1>d_{max}$であれば⑤へ、それ以外は⑥へ進みます。
➄ ノード追加:$D(i)$をノードに追加し勝者ノードを更新します。
ノードの年齢($Age_w=0$)とノードの活性値($A_w=0$)、パスの年齢($Age_s=0$)とパスの活性値($A_s=0$)を初期化します。
⑥ ノード更新:$D(i)$と第$N$勝者までの活性値$a_n$($n=1~N$)を求め、ノード位置、ノード活性値$Aw$、パス活性値$A_s$を更新します。
活性値$a_n$の計算式:$a_n=exp(\frac{-d^2}{d_{max}^2})$
$d$: ノード$n$とデータ$D(i)$間の距離
$d_{max}$:ノード間の最大距離(①の初期化で求まる値)
ノード活性値$A_w$の更新式: $A_w(n_1) += a_1$
パス活性値$A_s$の更新式: $A_s(n_1,n_2) += a_1\cdot a_2$
⑦ 生き残っているすべてのノードとパスの年齢を更新し($Age_w++$, $Age_s++$), 活性度$A_{rate}$を求めます。($A_{rate_w}=A_w/Age_w$ $A_{rate_s}=A_s/Age_s$)
⑧ $mod(i,指定間隔L)=0$の場合は、活性度$A_{rate}$が閾値を下回るパスとノードを削除します。
⑨ $i=M$なら終了、それ以外は$i=i+1$として③へ戻ります。
次に、①におけるハイパーパラメータの決定と初期ノードついて説明します。EXAMHELでは、最初にデータの統計的な性質を解析し、ハイパーパラメータを決定することで、安定した学習が可能となっています。ハイパーパラメータは、$N_n$:1ノードが代表するデータ数の目安、$N_{dw}$:ノード削除順位、$N_{ds}$:パス削除順位、の3つになります。
- 全データ(データ数$M$)について、距離の昇順に$N_n$番目の近傍データとの距離を求め、その平均値をノード間の最大距離$d_{max}$とします。
- 各データ($i=1~M$)について、各データをノードと仮定して、以下の計算を行います。
距離$d_{max}$以内の近傍データからノード活性度を計算し、配列$A_{rate_w}(i)$に代入します。
$A_{rate_w}(i)$ $i=1~M$、は1次元の配列で、全ノードの活性値が入ります。
$A_{rate_w}(i)$は、ノード$i$に属するデータのノード活性値の和を、年齢($M$)で割ったものです。
距離$d_{max}$以上離れたデータのうち最も距離が近い近傍データ$j$とのパス活性度を計算し、配列$A_{rate_s}(i,j)$に代入します。
$A_{rate_s}(i,j)$ $i=1~M$、$j=1~M$、は2次元の配列で、全パスの活性値が入ります。
$A_{rate_s}(i,j)$ は、パス$i-j$に属するデータのパス活性値の和を、年齢($M$)で割ったものです。 - 初期ノード$N$を以下のように計算します。
$A_{rate_w}$を降順にソートし、活性度の高い順から、初期ノードに追加します。
ただし、すでに追加したノードとの距離が$d_{max}$未満の場合は、追加しません。 - ノードとパスの削除閾値を以下のように計算します。
ノード削除閾値$=A_{rate_w}$を降順にソートし、指定された順位($N_{dw}$)の$A_{rate_w}$の値を閾値として設定します。
パス削除閾値$=A_{rate_s}$を降順にソートし、指定された順位($N_{ds}$)の$A_{rate_s}$の値を閾値として設定します。
3. EXAMHELを利用した教師なし学習
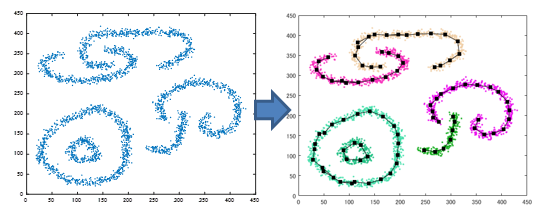
EXAMHELを利用すると、非線形なクラスタリングを行うことができます。図表 2はEXAMHELによるクラスタリング結果の例です。データのつながりを考慮した非線形なクラスタリングが実行できていることが分かります。
4. EXAMHELを利用した教師あり学習
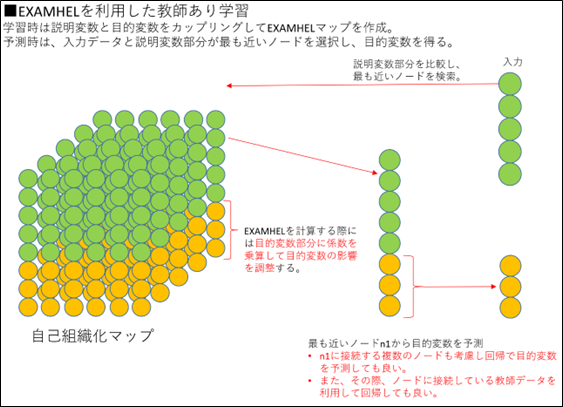
説明変数と目的変数をカップリングしてEXAMHELマップを作成することで、教師あり学習にも適用することができます。予測時には、入力データに最も近いノードを検索し、最近接ノードの目的変数を取り出せば、予測値が得られますので、予測値が得られた原因を説明することが可能です。
一般に非線形モデルは、予測精度が高い反面、説明性に難がある場合が多いのですが、EXAMHELマップは、非線形モデルでありながら、説明性が高いのが特徴です。
5. EXAMHELの活用事例:景気動向指数の分析
EXAMHELの有効性を検証するため、景気動向指数(CI一致指数)を推定する学習に適用してみました2。
当社が開発した変数選択手法RACSISを利用し、$3367$個の説明変数の中から選択した$26$個を用いてEXAMHELで学習したところ、目的変数と説明変数の関係を表す$19$個のノードからなるマップが得られました。
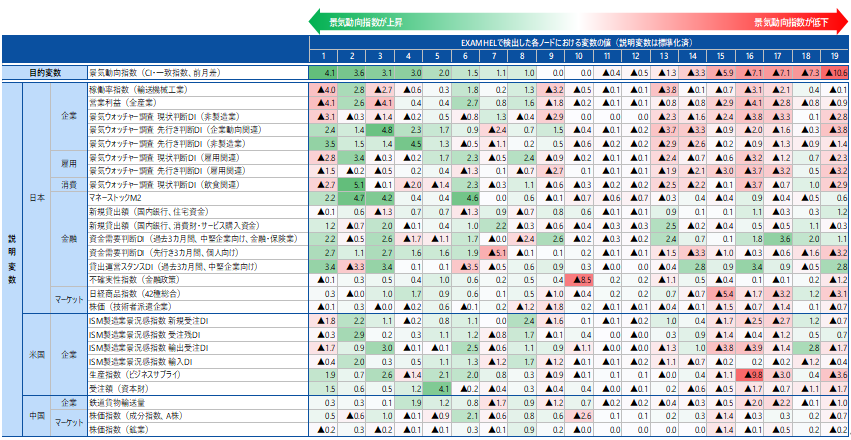
図表 4は、検出したノードについて、目的変数(景気動向指数の前月差)が大きい順に$1~19$の番号をつけ、各ノードにおける目的変数と説明変数の値を一覧にしたものです。
図表 4 EXAMHELマップの各ノードにおける目的変数と説明変数の値
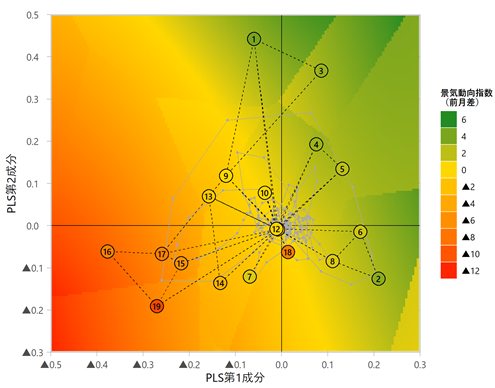
$26$次元の空間を部分的最小二乗回帰(PLS)により2次元に次元圧縮したものを図表 5に示します。一般的に次元圧縮には主成分分析(PCA)が用いられますが、PLSは目的変数と相関の高い主成分軸を求めることが可能であるため、今回のような回帰を行う場合は、PLSを用いる方が、目的に合致した次元圧縮を行うことが可能です。オレンジは景気が悪化している領域で、緑は景気が改善している領域です。図中の数字はノード番号を示しており、灰色の折れ線は、実際の景気変動について移動平均を取ったものです。
図表 5 景気動向指数のEXAMHELマップ(PLSにより2次元に圧縮)
(注)
1. ノード11はノード12とほぼ同じ位置にあり、マーカーが重なっている
2. 灰色の折れ線グラフは2005年3月~2021年9月の説明変数$26$系列をPLS第1・2成分に変換し、後方$3$カ月移動平均をとったもの
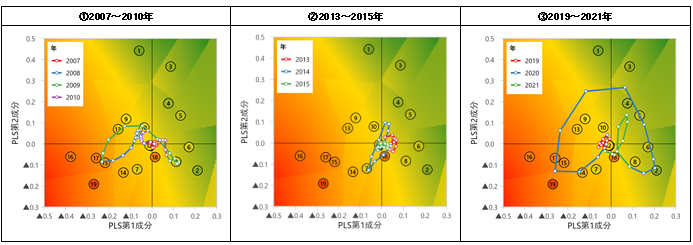
実際の説明変数の動きから過去の日本経済の局面を把握してみましょう(図表 6の①~③の折れ線グラフ)。
まず2008年には図表 6(①)の原点付近から左下のノード15方向に移動し、マーケットや海外部門も含め経済が全般的に悪化したことを示唆しています。米国のサブプライムローン問題に端を発するリーマンショックにより、海外経済や市場の悪化が日本の急速な景気後退につながった動きが現れていると言えます。一方、2009年には左上のノード13付近を経由して右下のノード8へ循環し、日米中の経済指標が改善したことを伺わせる動きとなっています。
次の図表 6(②)では、2014年に再び原点付近からやや左下のノード7方向に移動しています。これは、2014年4月に実施された消費税率引き上げ($5%$→$8%$)に起因するものであり、海外経済や市場の悪化を伴った2008~2009年の局面とは図中の位置が全く異なることが分かります。
その後、2019年までは原点付近で目立った動きはみられませんが、2020年には新型コロナの感染拡大に伴う都市ロックダウンで経済が急速に悪化し、2008年と同様に原点付近から左下へ移動しました(図表 6の③)。2020年後半にはロックダウン解除により景気が回復し、左下~原点上側~右下にかけて時計回りに大きく循環しました。左下・右上方向ともに2005年以降で最も外側の領域まで移動しており、コロナ禍初期における経済の落ち込みと回復の振幅が非常に大きかったことを示しています。なお、2020年の循環(図表 6の③)では2009年の循環(図表 6の①)に比べ、原点上側のノード1、3の近くを通っていることが確認できます。ノード1、3は日本の企業・雇用・消費指標がマイナスである一方、金融指標がプラスであることを示しており、コロナ禍における景気の改善が金融面の後押しに強く依存していたことを示唆しています。
このように、EXAMHELマップを利用すると、予測結果の因果関係を説明するだけでなく、学習したモデルを人間が解釈し、判断材料にすることが可能です。言い換えると、AIとヒトの協調を可能にするのがEXAMHELなのです。
6. まとめ
当社が開発した、説明性の高いAIであるEXAMHELについてご紹介しました。EXAMHELは、教師なし学習(クラスタリング)と、教師あり学習(回帰、分類)の両方に適用することが可能で、非線形な学習モデルでありながら説明性が高いという優れた特徴を持っています。
実際に、景気動向指数の予測に対してEXAMHELを活用し、学習モデルから様々な知見が得られることが示されました。今後も、様々な課題に対して、EXAMHELを適用し、機械学習の可能性を広げていきたいと考えています。
情報通信研究部 永田 毅
-
永田 毅、竹田 康亮、前川 秀正、世古 千博、小泉 拓、水谷 麻紀子、根本 裕也、橋本 大樹、森 悠史、玉垣 勇樹、岩渕 耕平、小永吉 健太、信夫 大志、学習システム、学習方法及び学習プログラム、特願2022-002464 ↩
-
みずほインサイト「AIが可視化する日本の景気変動─ 独自開発のホワイトボックス型AIによる経済分析 ─」(https://www.mizuho-rt.co.jp/publication/report/research/insight/2022/insight-jp221012.html) ↩