1.はじめに
RACSIS(Random Combination Selection with Iterative Step)1は、全く新しい変数選択手法です。本稿では、なぜ今新しい変数選択手法を開発したのか、その経緯と開発のヒントになった粘菌の研究に触れた後、RACSISの中身について述べ、その応用事例についてもご紹介します。
2. 機械学習の精度向上の鍵を握る変数選択
変数選択は機械学習で重要なテーマの一つですが、これまで、なかなか進展がなく、精度向上の大きな足枷となっていました。どうしてかと言うと、あまりに組み合わせが膨大過ぎて、全探索による最適解探索が困難だからです。説明変数の候補が$N$個ある場合、説明変数の組み合わせの数は、$2^N-1$個になるため、たった$16$個の説明変数でも、その組み合わせ数は$65535$通りとなってしまいます。
では、一般的な変数選択手法はどうしているかと言うと、説明変数単独での有効性を求めて降順にソートし、上位$K$個を選択する手法を取ることが多いです。例えば、LASSO2は線形重回帰における説明変数の重みを有効性の指標とする手法であり、BORUTA3はランダムフォレストにおいて説明変数をランダムにシャッフルして説明変数の重要度を求めて有効性の指標とする手法です。
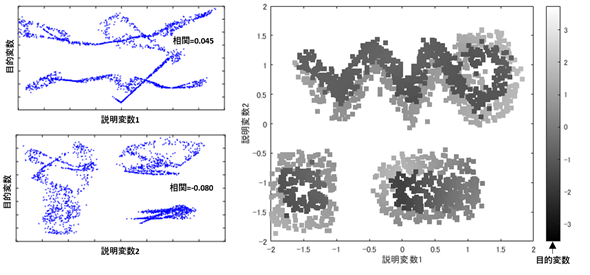
しかし、やっかいなのは、説明変数単独での有効性は低いけれども、組み合わせると有効な説明変数になるというものが存在するという点です。下図(単独では有効性が低いが、組み合わせると有効な説明変数の例)左側の2つのグラフは、あるデータの2つの説明変数を横軸に取り、縦軸に目的変数を取ったものですが、横軸の値が決まっても、縦軸の値は一意に決まらず、説明変数と目的変数の相関はほとんどないため、説明変数単独の有効性は非常に低くなります。右側のグラフは、横軸と縦軸に先ほどの2つの説明変数を取り、目的変数を色でプロットしたものです。このグラフより、この2つの説明変数が決まると目的変数が一意に決まり、かつ、色の分布に規則性があるため、機械学習で非常に高い精度の予測が可能であり、この2つの説明変数を組み合わせた場合の有効性は非常に高いことが予想できます。しかし、残念ながら、説明変数単独での有効性が高い変数を組み合わせる手法では、このような組み合わせを見つけられない場合があるのです。
3. 粘菌の最適解探索は凄い!
近年、自然界の最適解探索技術が注目を集めています。筆者が注目しているのは粘菌です。イグノーベル賞を2回も受賞された北海道大学電子科学研究所の中垣俊之先生の研究では、粘菌が迷路を解いたことが報告されています4。

迷路も最適解探索問題です。長さの短い通路を繋げていけば最適解が得られる、というわけでもありません。説明変数単独の有効性が高いものを選べばよいわけではない、という変数選択問題と似ていませんか?しかも、迷路は、通路の順番も重要なので、順番つき組み合わせ問題ですが、変数選択問題は、順番なしの組み合わせ問題なので、変数選択問題の方が簡単なはずなのです。
人間のように高度な知能を持ち合わせていない粘菌が高度なパズルが解ける、これは大きな驚きでした。粘菌は、迷路を満たした状態からスタートし、通路ごとに、自律分散的に、重要な通路は太くなり、そうでない通路は細くなり、最終的には最適解に到達したのです。
粘菌のような単純なルールに従う単細胞生物が、高度なパズルを解けるのならば、変数選択にも応用できるのではないか、筆者は直感的にそう感じ、RACSISの開発にとりかかりました。このようなわけで、RACSISの開発には、粘菌が大きなヒントになっています。粘菌は最初すべての経路を覆うように配置され、試行錯誤を繰り返す中で、不要な経路が細くなり排除されていき、最終的に最適解となる経路が残ります。RACSISも同様に、すべての説明変数を選択したところからスタートし、試行錯誤を経て、組み合わせの中で不要な説明変数を削除していきます。その具体的な処理について、次章で詳しく見ていくことにしましょう。
4.RACSISについて
RACSISは、前節で述べた、粘菌をヒントに、当社が独自に開発した変数選択手法であり、説明変数単独での有効性ではなく、組み合わせた場合の有効性をもとに変数選択を行います。ランダムに説明変数を選択して学習することを繰り返して、統計的に有効な説明変数の組み合わせを求めていきます。以下にその手順について説明します。
① 説明変数セット$M$の初期値として全変数を$M$に代入し、$M$で学習した場合の精度をベスト精度の初期値とし、ベスト説明変数の初期値を$M$とする。
② $M$の中から、ランダムに$P$%選択して学習し、その精度をRACSIS表の選択した説明変数に代入することを指定回数$N$回繰り返す。
③ 完成したRACSIS表を縦方向に平均を取り、説明変数ごとの平均精度$A_i$を求める。
④ 説明変数ごとの平均精度$A_i$の平均$A_{mean}$と標準偏差$A_{sd}$を計算し、$M$のうち、平均精度が、$A_{mean}-A_{sd}・Q$ 未満のものを削除し、$M$を更新する。
⑤ $M$で学習した場合の精度を計算し、ベスト精度を更新した場合はベスト精度とベスト説明変数を更新。
⑥ $M$の個数が$1$になった場合は終了。それ以外は、②に戻る。
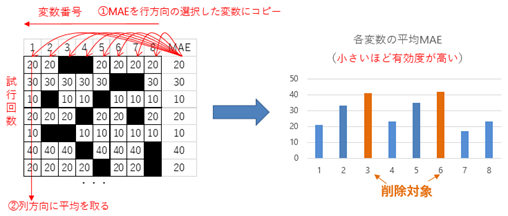
ここで、ステップ②、③、④におけるRACSIS表の作成と、説明変数削除のイメージについて、下図(RACSIS表の作成と説明変数の削除イメージ(説明変数が8個、$P=75$%の場合の例))を用いて説明します。RACSIS表は、行方向を説明変数方向、列方向を試行回数としたもので、ランダムに求めた説明変数の精度(MAE:平均絶対誤差)を表に代入していきます。もし、最適な説明変数の組み合わせが、選択した説明変数セットに含まれている場合、精度が良くなる可能性が高くなります。十分な試行回数の後、列方向に平均の精度を求めると、最適な説明変数の組み合わせの精度が高くなると期待されます。つまり、求めた平均精度が小さい程、各説明変数の組み合わせの有効性が高いことを示していると考えられます。粘菌の実験で言うと、好ましい経路は太くなり、そうでない経路は細くなるようなイメージです。
このように、RACSISは説明変数を組み合わせた場合の有効性を統計的に求めていくため、目的変数と説明変数の間に非線形な関係があったり、説明変数間の相互依存関係があったりしても、精度の高い説明変数の組み合わせが得られる可能性が高く、また、どのような機械学習手法にも適用できる汎用性を持っています。
5. RACSISによる景気動向指数の分析
RACSISの有効性を検証するため、景気動向指数を推定する学習に適用してみました。なお、この検証は、当社みずほリサーチ&テクノロジーズの情報通信研究部と調査部が共同で行った研究(以下、「本研究」とします。)です。当社の情報工学と経済・金融のスペシャリストが結集したことで、素晴らしい成果が得られています。
5.1. 分析の手順
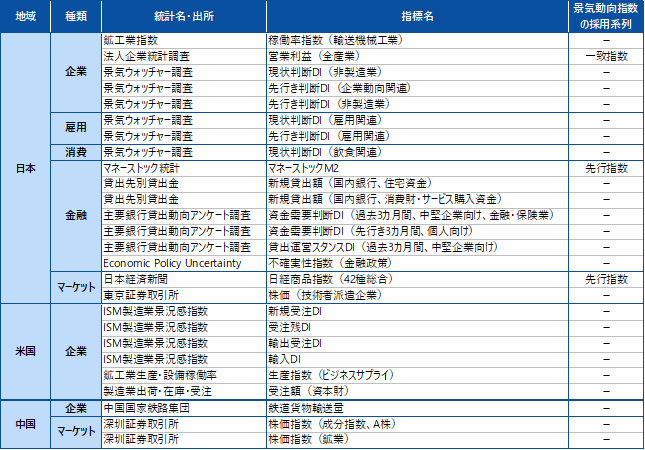
本研究では、2004年8月1日から 2021年9月1日までの$206$ヶ月分のデータを利用しました。下表に、本研究で用いた説明変数と目的変数について示します。説明変数の候補は、日本の景気動向に影響すると考えられる日本、米国、中国の経済・金融指標$481$個としました。なお、4章で説明したRACSISのパラメータは、$P=60$、$N=400$、$Q=1.25$に設定しました。
| 項目 | 説明 |
|---|---|
| 説明変数 (データ数$199$) |
$481$個の変数について、過去との差分を追加し、$481×7=3367$個の説明変数とした 当該月の値 当該月の値-$1$ヶ月前の値 当該月の値-$2$ヶ月前の値 ・・・ 当該月の値-$6$ヶ月前の値 |
| 目的変数 (データ数$199$) |
翌月の景気動向指数の変動 (当該月の翌月の景気動向指数-当該月の景気動向指数) |
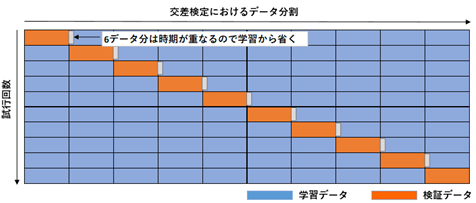
機械学習手法はSVR(サポートベクトル回帰)とし、RACSISで変数選択を行い、$10$-fold交差検証による精度検証を行いました。通常の交差検証では、教師データをシャッフルして行いますが、今回の場合、シャッフルすると、目的変数が同じ教師データの説明変数に含まれてしまい、正しい検証になりません。そこで本研究では、学習データと検証データ間でデータが重ならないように、データを連続的に取り、検証データと教師データの境界は、6ヵ月間空けるようにしました(下図($10$-fold交差検証のデータ分割イメージ))。
5.2. RACSISによる変数選択結果
RACSIS+SVRで変数選択を行った結果、$3367$個の説明変数から、下図(RACSISで選択した説明変数一覧)の$26$個の変数が選択されました。
選択された$26$個の説明変数による交差検証結果を下図(RACSIS+SVRによる景気動向指数推定結果($10$-fold交差検証))に示します。リーマンショックやコロナショックのように、事前に兆候があったと思われる落ち込みについては、かなり正確に予測できている一方、東日本大震災のような突発的な事象については、予測できておらず、モデルがオーバーフィッティングにならず汎化性能が高いことが分かります。

他の変数選択手法との比較を下表(各変数選択手法による交差検証精度比較)に示します。RACSISが最も精度が良いことが確認できます。
| 手法 | 選択説明変数の個数 | MAE(平均絶対予測誤差) |
|---|---|---|
| RACSIS+SVR | $26$ | $0.801$ |
| BORUTA+ランダムフォレスト | $30$ | $0.842$ |
| LASSO+SVR | $50$ | $1.027$ |
6. まとめ
当社が開発した、全く新しい変数選択手法RACSISについてご紹介しました。RACSISは、従来のように、説明変数単独での有効性を利用するのではなく、説明変数を組み合わせた際の有効性をもとに選択していますので、従来法では向上しなかったケースでも、精度の向上が期待できます。実際に、景気動向指数の予測に利用したところ、従来法よりも精度が向上することが確認できました。
今回は、SVRに対してRACSISを適用しましたが、RACSISはどのような機械学習手法にも適用できる汎用性を持っています。様々な課題に対して、RACSISを適用し、機械学習の可能性を広げていきたいと考えています。
情報通信研究部 永田 毅
-
永田 毅、竹田 康亮、前川 秀正、世古 千博、小泉 拓、水谷 麻紀子、根本 裕也、橋本 大樹、森 悠史、玉垣 勇樹、岩渕 耕平、小永吉 健太、信夫 大志、情報選択システム、情報選択方法及び情報選択プログラム、特願2022-002565 ↩
-
Tibshirani, R. (1996) “Regression shrinkage and selection via the lasso”, Journal of the Royal Statistical Society, Vol. 58(1), pp.267–288. ↩
-
Kursa, Miron B., and Witold R. Rudnicki. "Feature selection with the Boruta package." Journal of statistical software 36 (2010): 1-13. ↩
-
Nakagaki, T., Yamada, H. and Toth, A.(2000), Nature 407, 470. ↩