機械学習における精度向上のための工夫 ～外観検査アルゴリズムコンテストでの成果を振り返る～

1. はじめに

　筆者¹は2010年頃より、機械学習を取り入れた画像認識技術の研究開発に従事しており、腕試しに精密工学会画像応用技術専門委員会（IAIP）が主催する外観検査アルゴリズムコンテストに参加しています²。特に、2013年と2014年には、おかげさまで、2年連続で最優秀賞を受賞させていただくことができ、学会・業界に名前を知っていただくきっかけとなりました。かなり昔のことになってしまい恐縮なのですが、当時私が工夫した点を振り返ると、今でも参考になることが多いので、ここに記すことにしました。

2. 精度向上には、データと機械学習の性質を掴むことが重要！

　言わずもがなですが、機械学習で高い精度を達成するには、データと機械学習アルゴリズムの性質を掴み、両者の特徴が上手く噛み合うように誘導してあげることが重要です。何だかよく分からないが、大量のデータを機械学習器に入力すれば、勝手にAIがうまい具合に調理してくれる、ということは、まずないでしょう。

　2013年と2014年の外観検査アルゴリズムコンテストでは、自動車鋳造部品からの異常箇所の自動検出が課題となっており、特に2014年では、１部品に対して、カメラでラスタスキャンさせた連続撮影画像が事前に提供されていました。部品毎に連続撮影画像が210枚、正常部品2個+異常部品2個の計840枚という構成です。
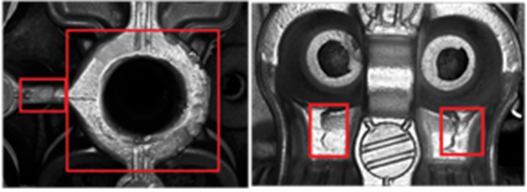
提供画像210枚から作成した鋳造部品のパノラマ画像の例を下図に示します。赤と黄の枠内が異常箇所を示しています。

　2014年当時は、まだ深層学習による画像認識が実用化されておらず、画像認識では、画像をパッチ分割し、パッチ単位でSIFT特徴量³とBag of Visual Words⁴を用いて画像特徴ベクトルを求め、SVM⁵でクラス分類することが主流でしたので、私も、この方法で課題に取り組むことにし、840枚の画像を、64x64のパッチ画像25万枚に分解して学習することにしました。
　しかし、学習する上で、２つの大きな問題がありました。一つは、異常領域が特定の領域に限定されており、異常パッチ画像が圧倒的に少ないこと、二つ目は、当時の私の計算機環境では、25万個もの教師データは多すぎて、とても学習しきれないことでした。この問題を、データと機械学習の性質を考慮しながら、どのように解決していったのか、次節以降で説明することにします。

3. 少ない異常データにおける機械学習の工夫

　ここでは、少ない異常データで機械学習の精度を向上させるために行った工夫について、説明します。

3.1. データ拡張

　異常データが少ない場合、現在では、まずデータ拡張（データの水増し）が頭に浮かぶと思いますが、2014年当時は、データ拡張はあまり認知されておらず、ノウハウもあまり蓄積されていませんでした。仕方なく、自己流でデータ拡張を行ったのですが、異常画像（下図）を確認すると、亀裂や歪みなど、画像処理的な水増し手法（画像の平行移動・回転・リサイズ・ノイズ付与等）でパターンを水増しできそうだということが分かりました。画像処理的な水増しについては、一般的な手法なので、これ以上の説明は不要だと思いますが、1点だけ、ここでコメントしておきます。今回採用した画像特徴量はSIFTになります。SIFTは、サイズや方向の違いに対して不変であるという特徴があります。よって、水増しする場合に、回転とリサイズによる水増しは不要だということが分かります。よって、私が試した水増しは、平行移動とノイズ付与になります。

3.2. 異常データの検知感度を敏感にする

　異常データを疑似的に水増しできましたが、あくまで提供された異常パターンの疑似データになりますので、未知の異常に対応できるのか、疑問が残りました。そこで、未知の異常データへの対応力を向上させるため、異常データの検知感度がより敏感になるように、正常と異常を識別する境界において、異常領域側のマージンを大きくとって異常データ領域を拡大することを考えました。この処理の詳細は、次節の内容が必要になるため、4.2節で議論します。

4. 膨大なデータから精度を落とさずに教師データを絞り込む工夫

　ここでは、データが多過ぎて全データでの学習が困難な場合に、精度を落とさずにデータを絞り込む方法について説明します。

4.1. 精度を落とさずに教師データを削減するステップ学習

　全データでの学習が困難な場合、一般的には、ランダムにデータを選択して学習することが多いと思います。しかし、全データによる学習よりも精度が劣化することが懸念されます。異常データが少ない場合、異常データは全データ採用することが可能だとしても、正常データは絞り込む必要があり、ランダムに正常データを選択すると、学習に重要なデータをオミットする可能性があるからです。
　では、どのようにして、機械学習の精度を落とさずに、教師データを絞り込むことが可能なのでしょうか？ここで重要なのが、「機械学習アルゴリズムの性質を掴む」という点です。今回のアルゴリズムは、SVMになります。SVMでは、正常と異常の境界付近に存在するデータ（サポートベクトルと呼ばれます）が、境界面を求める際に利用されます。逆に言えば、サポートベクトル以外のデータは、SVMの学習には不要です。もう、私が言いたいことはお分かりでしょう。そうです、サポートベクトルだけを収集すれば、学習精度を落とさずにデータを効率的に削減することが可能です。
　では、どのようにして、サポートベクトルだけを収集することができるでしょうか？本来、全データを学習しないとサポートベクトルは決まりません。でも、考えてみてください。境界付近のデータって、予測でミスしやすいデータですよね。だとすると、一部のデータで学習して、暫定的な境界を求めておき、その境界で予測に失敗したデータが、サポートベクトル候補と言えるのではないでしょうか？
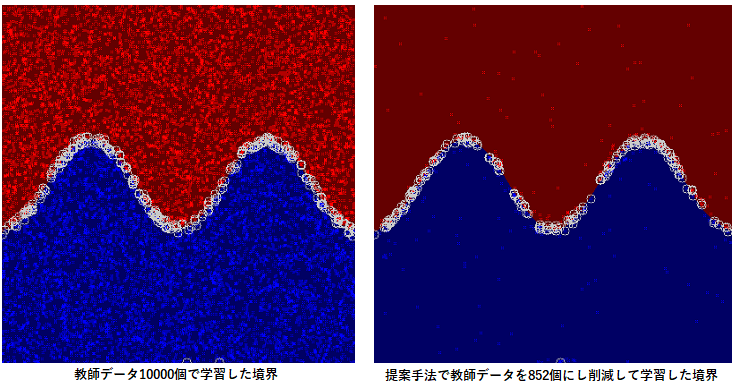
　このような発想で私が考案したのがステップ学習という手法です。例えば、1万個のデータがあり、これを500個ずつ20グループにランダムに分けておきます。そして、最初のグループ500個で学習して暫定境界を求めておき、2番目のグループ500個を予測し、予測に失敗したデータのみを最初の500個の教師データに追加して再学習して暫定境界を更新します。これを3番目以降のグループに対して逐次的に行えば、効率的にサポートベクトルが収集することができます。下図は人工的に作成した一万個の教師データで学習した場合（左）と、ステップ学習によって852個に削減して学習した結果を比較したものです。下図において、点が教師データ、〇がサポートベクトルを表しています。ほぼ同じようなサポートベクトルと識別境界が得らえていることが確認できます。このように、データと機械学習の性質を見極めることで、効率的に学習することが可能となります。

4.2. 異常データの追加確率の調整

　ステップ学習でデータを絞り込むことが可能となりましたが、サポートベクトル候補を追加する際に、すべてのデータを追加するのではなく、追加する確率を設定し、正常データと異常データで、異なる確率を与えたらどうなるでしょうか？SVMの場合、サポートベクトルが多いクラスの方が、領域面積が大きくなる傾向があることが知られています。もし、異常データの追加確率を、正常データよりも大きくすれば、異常データの領域が大きくなり、異常データの検知感度を向上させることができるのではないでしょうか？
　実は、一方のクラスの領域を拡大させる手法として、SVMでは、各クラスの重みを調整する手法が知られています。正常データよりも異常データの重みを大きくすれば、異常データの領域を拡大することが可能です。ただし、重みを調整すると、全空間において、一律に異常領域が拡大してしまい、正常データが欠陥と推定される可能性が高まり、実用的ではなくなる場合があります。
　私が提案した、追加確率を調整する手法は、こうした場合に有効です。予測に失敗したデータを追加する際に、異常クラスの確率を大きく設定すれば、必要な欠陥領域のみを拡大することに繋がります。下図は重みを調整した場合と追加確率を調整した場合の結果を比較したものです。水色〇が正常、黄+が異常データを表しています。教師データは、中央を境界として左右にランダムにデータを分布させ、中央の突起状の領域のみ、異常データと正常データが混在するように作成しました。よって突起状領域以外は中央が識別境界となるはずです。一律に重みを大きくした場合（左側）は、異常領域がすべて左方向に拡大してしまっているのに対して、提案手法の場合（右側）は、正常と異常が混在した突起状領域のみ左側に拡大しており、異常が疑われる領域はすべて異常と判定しつつ、正常データの誤判定は最小限に抑えることに成功しています。

5. まとめ

　2013年と2014年の外観検査アルゴリズムコンテストの受賞事例をもとに、データと機械学習アルゴリズムの性質を掴み、両者の特徴が上手く噛み合うように誘導するとはどういうことか、具体的に見てみました。精度を落とさずに教師データを削減する、正常データの誤検知リスクを抑えつつ異常データの検知感度を向上させる、といった工夫は、深層学習が主流となった現在でも参考になるのではないでしょうか？本記事が、温故知新となることを期待して、筆を置きたいと思います。

情報通信研究部　永田　毅

1. みずほリサーチ＆テクノロジーズ株式会社　情報通信研究部　永田　毅 ↩

2. http://alcon.itlab.org/ ↩

3. D. G. Lowe，"Object recognition from local scale-invariant features", Proc. IEEE International Conference on Computer Vision, pp.1150-1157, 1999. ↩

4. G. Csurka, C. R. Dance, L. Fan, J. Willamowski,and C. Bray，"Visual categorization with bags of key-points", Proc. ECCVWorkshop on Statistical Learn-ing in Computer Vision, pp.1-22, 2004. ↩

5. J.A.K. Suykens and J. Vandewalle, "Least Squares Support Vector Machine Classiers", Neural Process-ing Letters 9: 293-300, 1999. ↩