(ブログ記事からの転載)
1週間遅れですが、ABCで木構造の問題が解けなかったので、2度同じ間違いを繰り返さぬようメモります。
問題内容・解法
D - Ki
D - Ki

問題文その通りの考え方をすると、以下のように計算されていくことになります(ピンクの丸が頂点id、白い丸が値)。
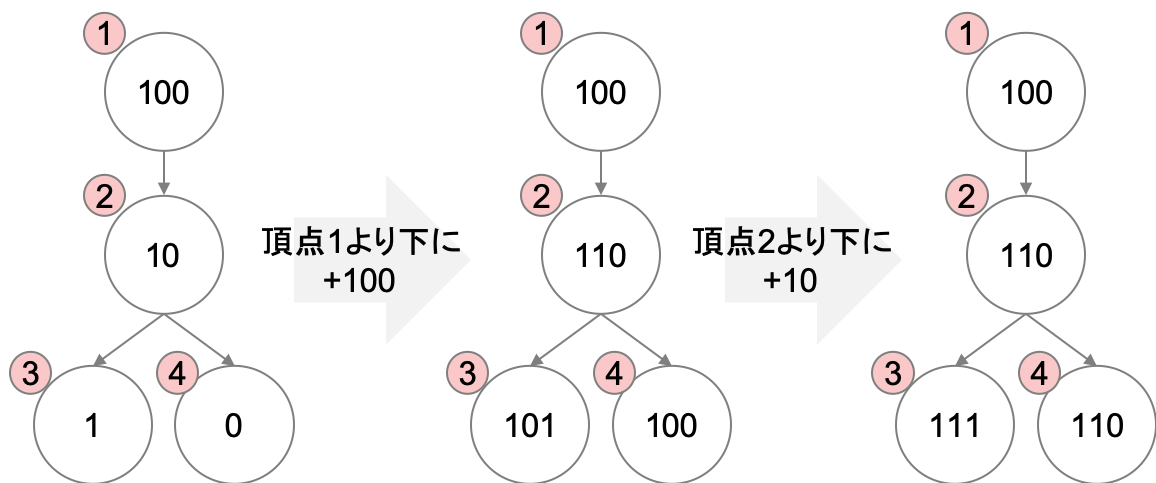
しかし、このロジックのまま実装すると何度も下層に降りて和を計算する必要があるため、非効率です。
このようなケースの常套手段として、累積和をとる方法があります。図にすると以下のような考え方です。
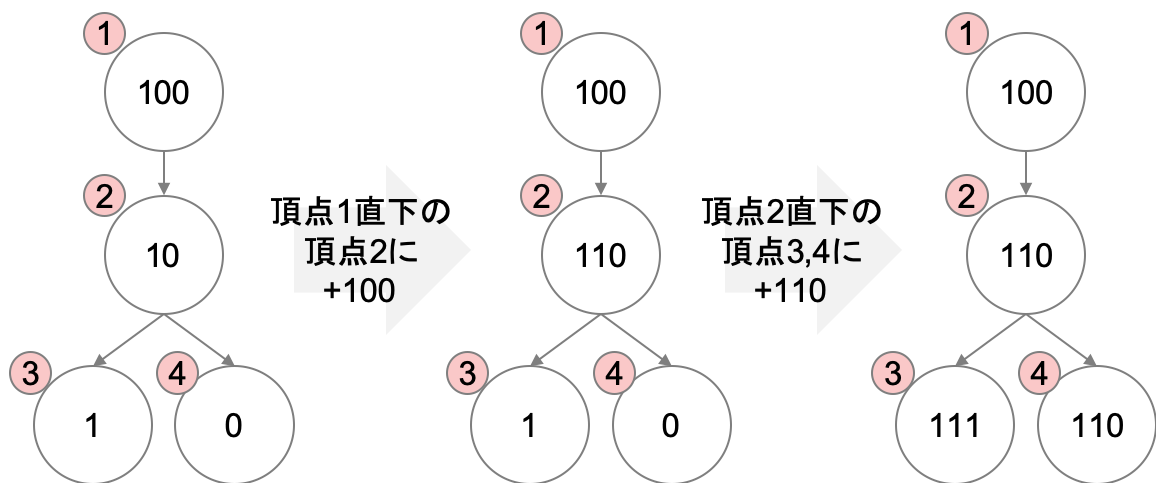
各頂点直下の頂点にのみ値を足し、足された値をまた直下の頂点に足すことで、結果的に問題文の指示通りの和が計算されることになります。
さて、このようにどんどん下層に降りていって和をとる問題なので、DFSを適用することになります。
コードは@dn6049949さんのものを多少改変して転載しています。
import sys
def LI(): return [int(x) for x in sys.stdin.readline().split()]
n,q = LI()
v = [[] for i in range(n)]
for i in range(n-1):
a,b = LI()
a -= 1 # listのindex参照をそのまま使いたいので頂点id(1から始まっている)を-1しておく
b -= 1 # aと同様
v[a].append(b)
v[b].append(a)
f = [0]*n
for i in range(q):
p,x = LI()
p -= 1 # aと同様
f[p] += x
def dfs(x,d,s): # x:計算する頂点(上側), d:計算済み(0)か否か(1), s:頂点xの値
for y in v[x]: # 頂点xとつながる各頂点yの計算を行う
if d[y]: # 頂点yが計算未了の場合
s += f[y] # 頂点xの値sに頂点yの値を足す
ans[y] = s # 頂点yの値はsに確定
d[y] = 0 # 頂点yの計算は終わったのでd[y]=0とする
dfs(y,d,s) # 頂点yの下層についても再帰的に計算
s -= f[y] # 頂点yの下層の計算が終わったので、sを頂点xの値に戻す
ans = [0]*n
d = [1]*n
d[0] = 0
ans[0] = f[0]
s = f[0]
dfs(0,d,s)
print(*ans)