幅優先探索を用いて迷路の最短手数を求めてみる

概要

迷路問題を解くときに使われるアルゴリズムの一種として、幅優先探索アルゴリズムがあります。
簡単な題材を元に解説し、最後に例題を掲載しますので、これを機に †完全に理解した†　になりましょう！

因みにこの記事は「Qiita Engineer Festa 2022」に向けて書きました。

今回の迷路問題を解く流れについては、@E869120さんが天才的な動画を作成していたので共有します！　　

例題

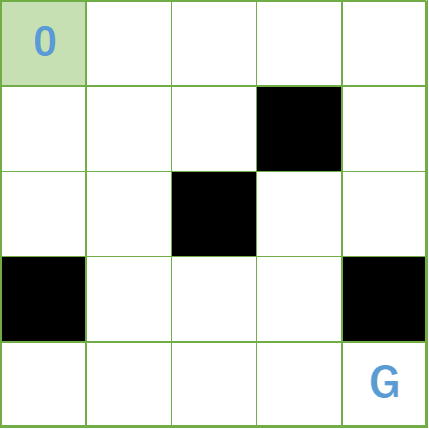
下記の迷路のスタート地点からゴール地点までの最短手数がいくつか求めなさい。ルールは下記のとおりとする。

• Sをスタート地点、Gをゴール地点とする。
• 移動は上下左右の4つの方向にしか進めない。
• 色がついている部分を"壁"とし、その方向には進むことは出来ない。
  

解き方

1. スタート地点は最短手数が0で到達できるので確定させる(背景色の緑が確定したことを示す)
   

2. スタート地点から1手で到達できる場所について、確定されていなければ1で確定させる
   

3. 2.で確定させたマスから1手で到達できるマスについて、確定されていなければ2で確定させる
   

4. 上記を繰り返し、確定させるマスがなくなったら終了させる
   

何がやりたいのかは、上記で共有した動画の流れと同じです。
現在地点から行けるマスで行ったことがなければ(確定していなければ)進んでいく方式です。

Queueを用いて実装する

この手順で実装する際にはQueueを使うことが知られています。
Queueとは 先入れ先出し(FIFO) のデータ構造で、先に入れたものを先に出す動作を高速に行うことができます。
Queueを使用し、

• 確定したマスを追加する
• 追加したマスを取り出し、1手で到達できるマスについて調べる

ことを繰り返し行っていくことで、上記の流れをプログラム上で再現できます。

因みにPythonではcollectionsモジュールのdequeがよく使用されます。
queueに比べて高速に動作するためです。

1手で到達できるかを調べる

これは意外と単純で、現在の地点を(h, w)とすると、

• 上のマスは、(h-1, w)
• 下のマスは、(h+1, w)
• 左のマスは、(h, w-1)
• 右のマスは、(h, w+1)

で求めることが出来るので、これをいい感じにコードに実装するだけです。　　
　　
自分の場合は単純なループだけで調べたいので、移動範囲を定義した下記の2つのリストを用意しています。

dh = [-1, 1, 0, 0]
dw = [0, 0, -1, 1]

これを下記のようなループで回してあげると、現在地点から上下左右のマスを求めることが出来ます。

for i in range(4):
  print(h+dh[i], w+dw[i])

今回の場合、移動後のマスが迷路の外になっていないか、壁にめり込んでいないか注意する必要があります。
応用問題

マス目の確定

マス目ごとの最短手数を持った配列を用意しておき、-1などで初期化しておきます。
移動先が-1であれば未確定なので、現在のマスの最短手数+1で確定させればOKです。

コードに落とし込む際の補足

入力の順番は下記のとおりとする。

• 迷路の大きさ (縦、横の順)
• スタート地点の情報
• ゴール地点の情報
• 迷路の情報
  • 迷路で進めるマスを.とし、壁を#とする
  • スタート地点とゴール地点は必ず.となる

上記の図の情報を入力する際には下記のように入力します。

5 5
0 0
4 4
.....
...#.
..#..
#...#
.....

Pythonでの実装

from collections import deque


def main():
    H, W = map(int, input().split())
    sh, sw = map(int, input().split()) # スタート地点
    gh, gw = map(int, input().split()) # ゴール地点
    Field = [list(input()) for _ in range(H)] # 迷路情報
    dist = [[-1] * W for _ in range(H)] # 最短手数情報
    dh = [1, -1, 0, 0]
    dw = [0, 0, -1, 1]

    Q = deque()
    # スタート地点を確定させ、マス目の情報をキューに格納する
    dist[sh][sw] = 0
    Q.append((sh, sw))
    while Q:
        h, w = Q.popleft()
        for i in range(4):
            next_h = h + dh[i]
            next_w = w + dw[i]
            if 0 <= next_h < H and 0 <= next_w < W and Field[next_h][next_w] == ".":
                if dist[next_h][next_w] == -1:
                    dist[next_h][next_w] = dist[h][w] + 1
                    Q.append((next_h, next_w))
    
    print(dist[gh][gw])


if __name__ == "__main__":
    main()

例題

解けないのが当たり前ぐらいの気持ちでやってみましょう！(本当に慣れていないと難しいので…)

迷路関連

• ATC001-A
  • 典型的な迷路問題
• ABC151-D
  • 一応迷路
• ABC176-D
  • 迷路…？
• ABC213-E　
  • 難しいが、ここで学んだ迷路と異なる点に着目しよう
• 典型090-043
  • 変わった迷路問題。面白いのでおすすめ(なかなか難しい)

幅優先探索関連

• アルゴ式
  • ここに幅優先探索の教科書があるので、見ておくことをお勧めします。
• AOJ
  • AOJの幅優先探索の例題。
  • 右上の虫眼鏡マークから他人の解法が見れるので、分からなかったら覗いてみよう！
• ABC224-D
  • こういう最短手数を求めるゲームも幅優先探索で解くことができる(めちゃくちゃ難しい)

幅優先探索はめちゃくちゃ活用場所が多いので、上記のような典型を覚えるだけで力になります。

終わりに

今回は迷路問題を解く幅優先探索アルゴリズムについての記事を書きましたが、世の中にはもっと面白く画期的なアルゴリズムが存在しています。
幅優先探索と一緒に語られる深さ優先探索アルゴリズムなどもありますので、興味がある方は一度調べてみてはいかがでしょうか！