はじめに
主成分分析はデータを縮約する手法であり、たくさんの変数があるようなデータについて、傾向等を分析するのに役立ちます。個人的な話で恐縮ですが、最近、主成分分析を使いたいと思う場面が何度かありましたので、この機会に流れをおさらいしてみたいと思います。
自分用のメモです。
※ 2023/09/08 コメントで貴重なご指摘をいただき、記事を修正しました(@WolfMoon 様、ありがとうございます)。詳しくはコメントをご確認ください。
環境
R ver 4.2.1 を用います。なお、パッケージは、なるべく組み込みのものを利用する方針で行きます。
参考資料
以下の2つの資料を参考にしました。
主成分分析の分析の流れ
データの準備
今回は、各市町村ごとの「指定緊急避難場所」の指定個所数を分析します。指定緊急避難場所は、災害対策基本法第49条の4に基づいて、市町村長が「異常な現象の種類」毎に指定します。異常な現象は、以下の8種類です。
- 洪水
- 崖崩れ、土石流及び地滑り
- 高潮
- 地震
- 津波
- 大規模な火事
- 内水氾濫
- 火山現象
各市町村ごとの指定緊急避難場所のデータは、国土地理院から CSV で提供されているので、こちらを用います(作業時は2023/08/31版でした)。
この CSV データは、各指定緊急避難場所毎のデータとなっているので、Excel のピボットテーブルで各市町村毎・種別毎の合計として集計した結果を skhb-230831-table.csv という名前で保存しておきます。
なお、8種類の異常な現象の他、「指定避難所との住所同一」かどうかの情報も含まれているので、こちらも利用します。また、データ識別のため、市町村コードと市町村名も含めます。
データの読込
準備した skhb-230831-table.csv を R で読み込みます。
df <- read.csv("./data/skhb-230831-table.csv", header=TRUE)
# 空白(NA)を0に置き換え
df[is.na(df)] <- 0
# 必要なデータのみを取り出す
tdf <- df[,c(3:11)]
# 市町村コードと祖町村名を行名に設定
rownames(tdf) <- paste(df[,1], df[,2], sep="-")
以下は、参考にデータの中身です。
head(df)
# 市町村コード 都道府県名及び市町村名 合計...洪水 合計...崖崩れ.土石流及び地滑り 合計...高潮 合計...地震 合計...津波 合計...大規模な火事 合計...内水氾濫 合計...火山現象 合計...指定避難所との住所同一
# 1 1202 北海道函館市 49 73 0 135 170 0 0 9 81
# 2 1203 北海道小樽市 20 37 0 42 19 2 0 0 37
# 3 1204 北海道旭川市 53 53 1 53 0 52 66 0 16
# 4 1205 北海道室蘭市 251 238 0 0 185 0 0 0 4
# 5 1206 北海道釧路市 0 0 0 0 153 0 0 0 33
# 6 1207 北海道帯広市 57 3 0 105 0 54 0 0 102
下処理を全て R で行う場合
Excel を利用せずに、R で集計処理も行う方法をコメントで教えていただきましたので記載いたします。split() と sapply() を組み合わせるテクニックです。なお、読み込むデータは、国土地理院から取得してきた CSV そのものとなります。
df <- read.csv("全国指定緊急避難場所データ.csv")[c(1,6:14)];
df[is.na(df)] <- 0
gdf <- split(df, df$市町村コード)
tdf <- t(sapply(gdf, function(x) colSums(x[2:10])))
主成分解析の実行
主成分分析は、prcomp() を用います。特に理由がなければ、scale=TRUE としておいた方が良さそうです。
pca <- prcomp(tdf, scale=TRUE)
結果については、各サンプル(今回の場合は市町村ごと)の各主成分特典は pca$x に、各変数の固有ベクトルは pca$rotation に入っています。(str() で結果のデータ構造を確認できます。)
また、以下の通り結果を把握することができます。
# 実行結果を表示
summary(pca)
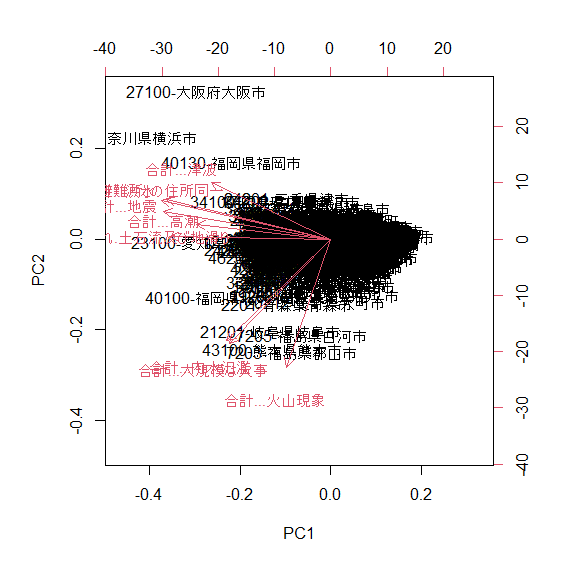
biplot(pca)
上記の実行結果は以下の通りです。
# Importance of components:
# PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9
# Standard deviation 2.2101 1.1520 0.86596 0.79612 0.7530 0.67252 0.42573 0.32817 0.31078
# Proportion of Variance 0.5427 0.1474 0.08332 0.07042 0.0630 0.05025 0.02014 0.01197 0.01073
# Cumulative Proportion 0.5427 0.6902 0.77348 0.84391 0.9069 0.95716 0.97730 0.98927 1.00000
第1主成分で寄与率約54%、第2主成分が約15%といったことが分かります。また、グラフ(biplot)から、多くの変数が第1主成分に影響していそうです。第2主成分を見ると、内水氾濫、大規模な火事、そして特に火山が影響していそうだと読み取れるほか、津波(主に海岸での被害が多い)と火山(主に内陸での被害が多い)が逆方向を向いていることがわかります。
因子負荷量の計算
各因子負荷量は prcomp() には直接記述されていないので、以下のように計算で出す必要があります。
ld <- sweep(pca$rotation, MARGIN=2, pca$sdev, FUN="*")
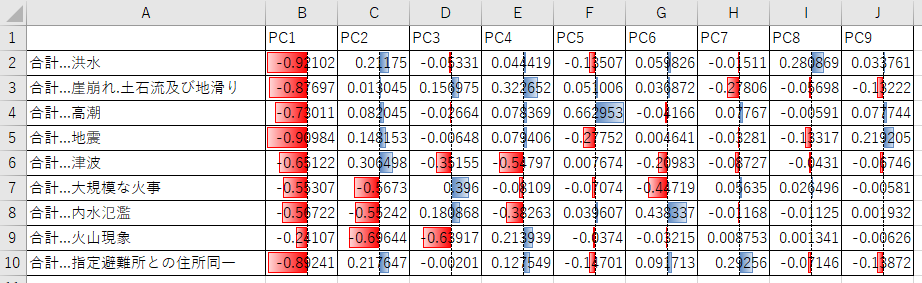
因子負荷量の図示ですが、CSV 出力して Excel に取り込み、Excel の条件付き書式の「データ バー」で表形式と棒グラフを組み合わせる形で図示するのが分かりやすいのではないかと思います。
write.csv(ld, "loadings.csv")
主成分の選択
岩田先生の講義資料を確認すると、有効な主成分数を決めるための簡単なルールが紹介されています。
- 累積寄与率が、ある定められた割合を超える主成分数を採用する。定められた割合として 70%〜90%の値が使われることが多い。
- 寄与率が、元の変数1つあたりの平均説明力を超える主成分を採用する。変数の数が q の場合、寄与率が 1/q を超える主成分を採用する。
- 相関行列の場合、上のルールでは“固有値が 1 を超える”主成分が採用される。しかし、この基準は厳しすぎる場合が多い。0.7 程度が適当であるという報告もある。
- 固有値のグラフで、急な変化からなだらかな変化に変わる点を採用する主成分とする。
個人的には、1.の累積寄与率を見ることが多かったですが、微妙な判断になることが多いです。例えば、ある主成分までで累積寄与率が78%の時、次の主成分を含めるかどうか?は悩むことになりそうです。事前に決めておけばよいのですが、事前に決めておかないで結果を見ると恣意的になりそうな気がします……。
そのため、2.か3.のルールが魅力的です(3.で固有値の基準を1とした場合は、2.と3.は一緒になります。)。これでは厳しいという意見もあるようですが、こちらを採用して今回の主成分を選択すると、
- Standard deviation(固有値の平方根に相当)が1以上
- Proportion of Variance(寄与率)が 100/9 = 11.1% 以上
が基準となりますので、第2主成分までが選ばれるということになります。(結果論ですが、4.の方法にも合致する選び方になります。)
この後は、今選択された主成分を用いて分析を続けていく、という流れになりそうです。
追加の分析
選択した主成分を用いて、どのような分析ができるか考えてみます。
クラスタリングによるグループ分け
選ばれた主成分を用いてクラスタリングを行ってみます。階層的クラスタリングの実行は以下のコードで実行できます。
dist <- dist(pca$x[,c(1:2)])
hc <- hclust(dist, "ward.D2")
# 樹形図の表示
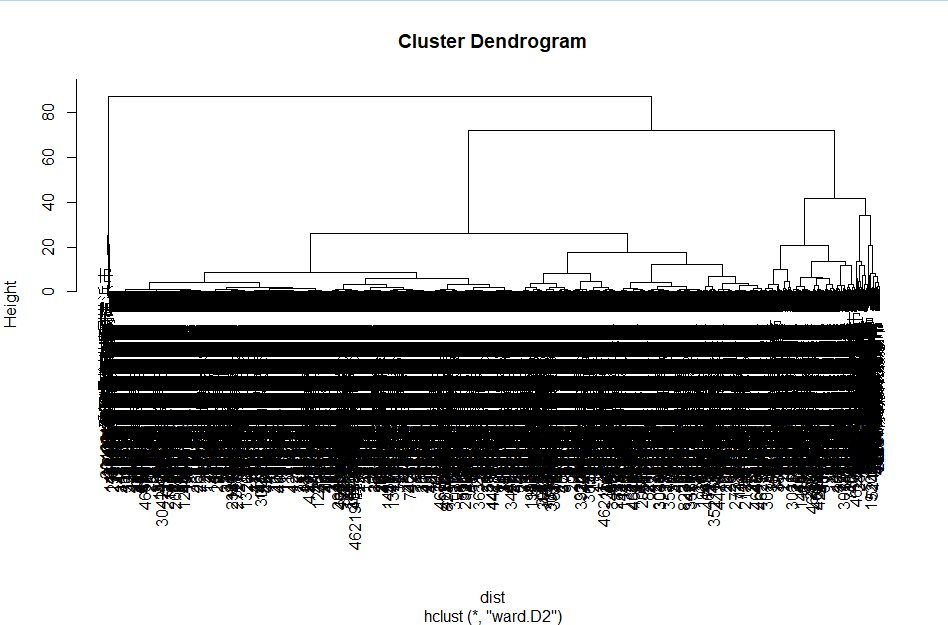
plot(hc)
樹形図を見て、適当なサイズ(今回は h=60 )で枝を切って、グループ分けをします。今回、データの加工はここまでなので、CSV へ出力しておきます。
g <- cutree(hc, h = 60)
# 元のデータにグループ分け(と主成分分析の結果)を統合
odf <- cbind(df, g, pca$x)
# CSV へ出力
write.csv(odf, "output.csv")
グループ分けを反映した biplot の作成
グループを記載したデータができましたので、各グループごとに、変数や主成分の平均値等を比較する場合は、aggregate() という関数が利用できます。
aggregate(odf, by=list(odf$g), mean)
# 各グループを構成するサンプル(今回は市町村)を表示
rownames(subset(odf,odf$g==1))
rownames(subset(odf,odf$g==2))
rownames(subset(odf,odf$g==3))
また、グループの情報を用いて、改めて第1主成分と第2主成分の biplot を作成してみます。
# プロットしたい主成分と主成分負荷量図示時の倍率指定
n1 <- 1; n2 <- 2; scale <- 10;
# 各サンプルの主成分得点をグループごとに色と形を変更して表示
plot(pca$x[,n1], pca$x[,n2], pch=g+1, col=g+1, main=paste("PC", n1, "vs", n2))
# 変数の主成分負荷量を図示
arrows(0, 0, ld[,n1]*scale, ld[,n2]*scale, pch="+", col="black", length=0.05)
# 変数名を表示
text(ld[,n1]*scale*1.1, ld[,n2]*scale*1.1,rownames(ld),col="black", cex=0.5)
なお、特定のサンプル名(ここでは自治体名)を表示するには、以下のようなコードでできます。
# 例:第2主成分が -7 以下のサンプルを抽出
a <- subset(pca$x, pca$x[,2] < -7)
# サンプル名を表示
text(a[,1], a[,2], rownames(a), cex=0.5, col="grey")
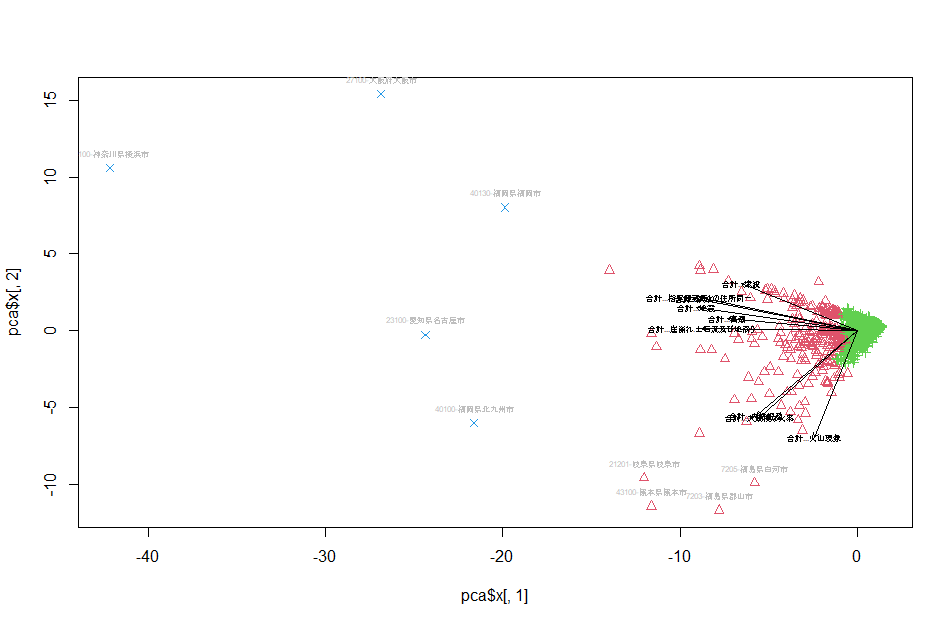
表示結果は以下の通りです。(自治体名の表示は、上記のコードによらず微調整しています。)
上記のグラフからは、指定緊急避難場所の指定数に応じてグループが分かれたようです。指定の内容(例:津波と比較して火山の指定が多い)などで分かれてくれることを期待しましたが、その観点ではうまくいきませんでした。
ちなみに、グループ3(第1主成分が特に大きいところ)は以下の通りです。どこも指定数が多いです。
14100-神奈川県横浜市、23100-愛知県名古屋市、27100-大阪府大阪市、40100-福岡県北九州市、40130-福岡県福岡市
第2主成分の小さい(-7以下)は以下の通りです。どこも火山の指定が多いです。
7203-福島県郡山市、7205-福島県白河市、21201-岐阜県岐阜市、43100-熊本県熊本市
他の変数との相関分析
今回は例示しませんが、主成分をデータセットの代表地として、他のデータとの相関を取るなどの分析ができるかもしれません。
例として、微生物の群集構造を主成分解析し、得られた主成分を他の変数(例えば、土壌の栄養分等)との相関を見る、といった分析辞令を見たことがあります。
感想
とりあえず、手ごろなデータで分析の流れをざっと整理してみました。もう少し面白い分析ができたら、この記事は大幅改訂(書き直し)するかもしれません。
(追記)せっかくコメントをいただきましたので、その知見を活かして、もう少しいろいろな角度から分析を加えられればと思います。