この記事はアドカレに参加しています。
ico球の面を求める
球を疑似的に表現する方法はいくつかありますが、その一つにico球があります。サッカーボールみたいなやつです。

文献
ICO球の作り方(1)
Creating an icosphere mesh in code
上記のリンク先が参考になりますが、今回は再帰処理を使って記述していきます。
アルゴリズム
-
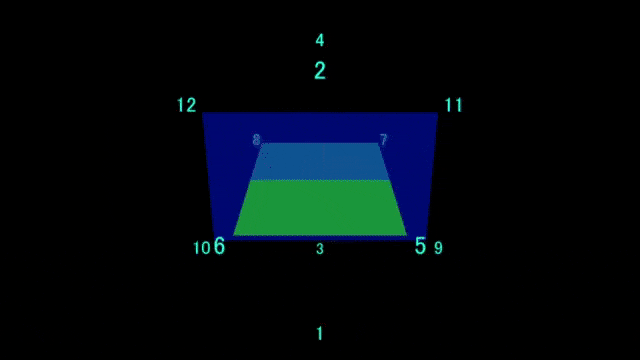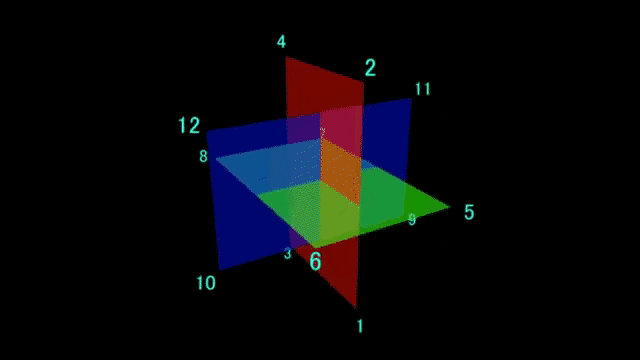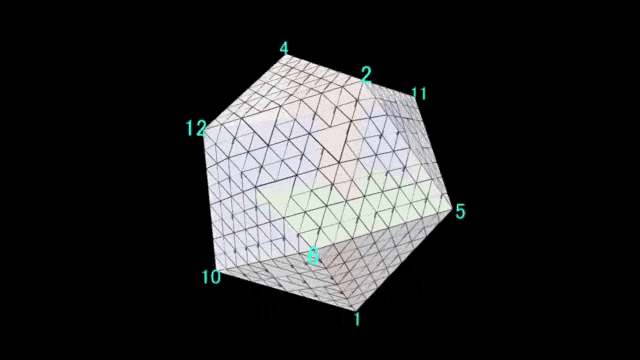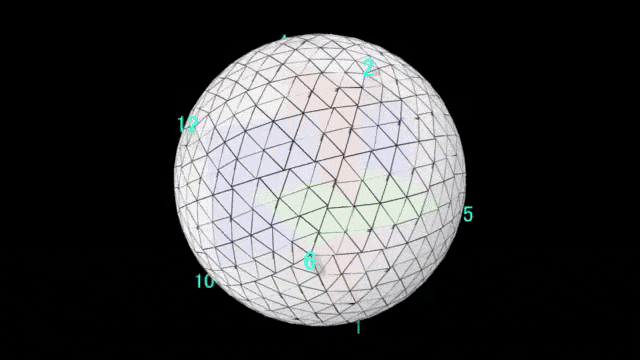
まずは、各頂点の座標を求めます。1:(1+√5)/2 の比率の長方形を三枚思い浮かべたとき、各長方形の頂点をそのまま使います。
-
次に、この頂点をもとに三角形を作ります。
このとき、三角形を任意の回数で分割していきます。 -
最後に、三角形の頂点と原点からの距離を調整します。
以下の動画のように進めていきます。twitterだとヌルヌル動いて分かり易いかもしれないですね。
コード
以下にaviutlで使用できるコードを示します。(注:以下のコードは古いものですので、バグがあります。完全なものを作成したい場合はこちらを参考にしてください。)
<?--こっちはテキストボックスとかに貼り付けておく
--変数
MR=100--半径
MS=1--[[再帰回数(0~5ぐらいが目安。大きすぎるとフリーズ)]]
MS=math.max(0,math.floor(MS))
MK=math.sqrt(MR*MR)/(2^MS)+1
--長さをもとめる関数
local function sn(x,y,z)
return math.sqrt(x*x+y*y+z*z)
end
--長さをMRにする関数
local function se(k)
local q=math.sqrt(k[1]*k[1]+k[2]*k[2]+k[3]*k[3])
k[1]=k[1]*MR/q
k[2]=k[2]*MR/q
k[3]=k[3]*MR/q
return k
end
--二地点の中点を求める関数
local function sl(w,e)
local d={}
d[1]=(w[1]+e[1])*0.5
d[2]=(w[2]+e[2])*0.5
d[3]=(w[3]+e[3])*0.5
return d
end
--描画関数
local function sd(a,b,c)
obj.load("figure","四角形",0xffffff,1)
obj.alpha=0.95
a,b,c=se(a),se(b),se(c)
obj.drawpoly(a[1],a[2],a[3],
b[1],b[2],b[3],
c[1],c[2],c[3],
c[1],c[2],c[3])
end
--頂点をもとに描画
function sa(a,b,c)
local k=sn(a[1]-b[1],a[2]-b[2],a[3]-b[3])
if(k<MK)then
sd(a,b,c)
else
local ab,ac,bc=sl(a,b),sl(a,c),sl(b,c)
sa(a,ab,ac)
sa(b,ab,bc)
sa(c,ac,bc)
sa(ab,ac,bc)
end
end
?>
--こっちは図形(四角形)にスクリプト制御から貼り付け
local r,yr
r=MR/2
yr=(1+math.sqrt(5))/2*r
local p={}
--二十面体の頂点を求める
p[1]={r,yr,0}
p[2]={r,-yr,0}
p[3]={-r,yr,0}
p[4]={-r,-yr,0}
p[5]={yr,0,r}
p[6]={yr,0,-r}
p[7]={-yr,0,r}
p[8]={-yr,0,-r}
p[9]={0,r,yr}
p[10]={0,r,-yr}
p[11]={0,-r,yr}
p[12]={0,-r,-yr}
--頂点をもとに描画
sa(p[2],p[4],p[11])
sa(p[2],p[4],p[12])
sa(p[2],p[6],p[12])
sa(p[2],p[5],p[11])
sa(p[4],p[8],p[12])
sa(p[4],p[7],p[11])
sa(p[2],p[5],p[6])
sa(p[4],p[7],p[8])
sa(p[1],p[5],p[6])
sa(p[3],p[7],p[8])
sa(p[6],p[10],p[12])
sa(p[8],p[10],p[12])
sa(p[5],p[9],p[11])
sa(p[7],p[9],p[11])
sa(p[1],p[6],p[10])
sa(p[1],p[5],p[9])
sa(p[3],p[8],p[10])
sa(p[3],p[7],p[9])
sa(p[1],p[3],p[9])
sa(p[1],p[3],p[10])
バグの修正とか
上に示したコードはバグがあるので、それを直す必要があります。
こちらにあるc言語で書かれたコードがバグ修正されています。変更点としては、
・描画時に頂点が時計回りになるようにした。
・再帰処理の終了判定が曖昧だったため、しっかりと変数でカウントするようにした。
…の二つです。
本当はluaもコードも直した方がいいけど、めんどいんや、、、
最後に
本来は、重い処理を再帰処理で書くのは良くないことです。ですが、今回はたのしいので再帰処理で書きました。いつか機会があれば、再帰処理を使わない処理も書いてみたいですね。
