この記事はアドカレに参加しています。
任意軸回転をやってみる
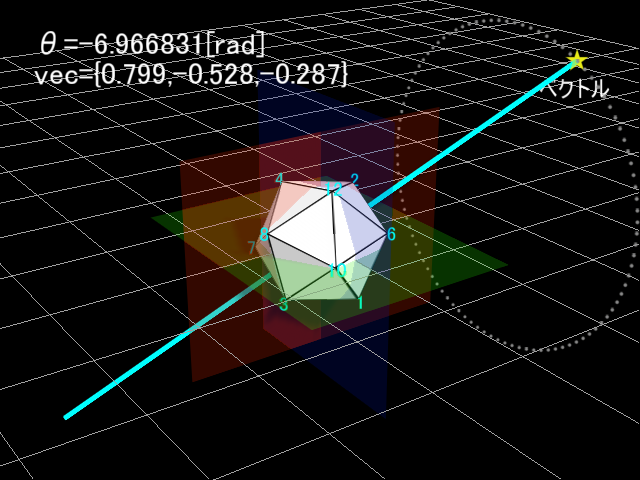
任意軸回転というものがあります。その名の通り、三次元空間で任意軸まわりに回転するやつです。
理論
さて、任意軸回転ということでクォータニオンについて理解する必要があります。
僕はあまり解説が上手くない&僕も理解していないので、クォータニオンの解説は以下のリンクなどをご参照ください。
クォータニオン (Quaternion) を総整理! ~ 三次元物体の回転と姿勢を鮮やかに扱う ~
クォータニオンとは何ぞや?:基礎線形代数講座
クォータニオンを使ったカメラの回転
回転行列、クォータニオン(四元数)、オイラー角の相互変換
実装
luaで書くと以下のようになります。
local th=(60)*math.pi/180--角度(ラジアンをthに
local bec={0,1,0}--三次元ベクトル
--単位ベクトルにする
local k=math.sqrt(bec[1]*bec[1]+bec[2]*bec[2]+bec[3]*bec[3])
bec[1]=bec[1]/k
bec[2]=bec[2]/k
bec[3]=bec[3]/k
--四次元ベクトルを用意
local q={}
local q2={}
q[1]=bec[1]*math.sin(th*0.5)
q[2]=bec[2]*math.sin(th*0.5)
q[3]=bec[3]*math.sin(th*0.5)
q[4]=math.cos(th*0.5)
q2[1]=bec[1]*math.sin(-th*0.5)
q2[2]=bec[2]*math.sin(-th*0.5)
q2[3]=bec[3]*math.sin(-th*0.5)
q2[4]=math.cos(-th*0.5)
--クォータニオンの掛け算
local function MultiplyQuaternion(q,p)
local d={}
d[1]=q[4]*p[1]-q[3]*p[2]+q[2]*p[3]+q[1]*p[4]
d[2]=q[3]*p[1]+q[4]*p[2]-q[1]*p[3]+q[2]*p[4]
d[3]=-q[2]*p[1]+q[1]*p[2]+q[4]*p[3]+q[3]*p[4]
d[4]=-q[1]*p[1]-q[2]*p[2]-q[3]*p[3]+q[4]*p[4]
return d
end
--この関数に座標を与えると、回転後の座標を返す
function rot_MQ(o)
local p={o[1],o[2],o[3],0}
p=MultiplyQuaternion(q,p)
p=MultiplyQuaternion(p,q2)
o[1],o[2],o[3]=p[1],p[2],p[3]
return o
end
解説
上記コードの解説をします。
まず、ベクトル(任意軸)と回転量を決めます。
local th=(60)*math.pi/180--角度(ラジアンをthに
local bec={0,1,0}--三次元ベクトル
次に、ベクトルを単位ベクトルにします。これはクォータニオンの定義に関わってくるので、単位ベクトルにするのを忘れてしまうと正確な処理をしてくれません。
--単位ベクトルにする
local k=math.sqrt(bec[1]*bec[1]+bec[2]*bec[2]+bec[3]*bec[3])
bec[1]=bec[1]/k
bec[2]=bec[2]/k
bec[3]=bec[3]/k
次は四次元ベクトルを用意します。あとで使うので、回転量に-1を乗算したベクトルも用意しておきます。
--四次元ベクトルを用意
local q={}
local q2={}
q[1]=bec[1]*math.sin(th*0.5)
q[2]=bec[2]*math.sin(th*0.5)
q[3]=bec[3]*math.sin(th*0.5)
q[4]=math.cos(th*0.5)
q2[1]=bec[1]*math.sin(-th*0.5)
q2[2]=bec[2]*math.sin(-th*0.5)
q2[3]=bec[3]*math.sin(-th*0.5)
q2[4]=math.cos(-th*0.5)
クォータニオン同士の掛け算を行う関数です。
--クォータニオンの掛け算
local function MultiplyQuaternion(q,p)
local d={}
d[1]=q[4]*p[1]-q[3]*p[2]+q[2]*p[3]+q[1]*p[4]
d[2]=q[3]*p[1]+q[4]*p[2]-q[1]*p[3]+q[2]*p[4]
d[3]=-q[2]*p[1]+q[1]*p[2]+q[4]*p[3]+q[3]*p[4]
d[4]=-q[1]*p[1]-q[2]*p[2]-q[3]*p[3]+q[4]*p[4]
return d
end
最後に、回転後の座標を求める関数です。
入力座標を四次元ベクトルとして計算していきます。
--この関数に座標を与えると、回転後の座標を返す
function rot_MQ(o)
local p={o[1],o[2],o[3],0}
p=MultiplyQuaternion(q,p)
p=MultiplyQuaternion(p,q2)
o[1],o[2],o[3]=p[1],p[2],p[3]
return o
end
さて、作成した関数に三次元の座標を渡すと、回転後の座標が返ってきます。
local testpos={100,50,200}
local testpos2=rot_MQ(testpos)
最後に
discordにサンプルプロジェクトを投げているので、興味のある方は是非。