- 授業で習ったことをまとめるメモ
線形代数のおさらい
1. n次元の空間は、n個の基底ベクトルで表される
下の図の場合、2次元平面上の任意の点P$(\vec{r})$は、2つの基底ベクトル $\vec{a}, \vec{b}$ の線型結合で表される
$$\vec{r} = c_1 \vec{a} + c_2 \vec{b}$$

(http://web1.kcg.edu/~k_emi/math/LA/chap1/LA112.htm )
一般には、
$$\vec{e_1}, \vec{e_2}, \cdots, \vec{e_n}$$ を基底ベクトルとすると、
$$\vec{r} = c_1 \vec{e_1} + c_2 \vec{e_2} + \cdots + c_n \vec{e_n}$$
と表される. ここで、$$c_1, c_2, \cdots, c_n$$は、各基底ベクトルの**”重み付け”**と考えることができる.
2. ベクトルの内積
2つの複素n次元ベクトル
$$\vec{a} = (a_1, a_2, \cdots, a_n), \vec{b} = (b_1, b_2, \cdots, b_n)\in \mathbb{C}$$ の内積は、
\begin{align}
\vec{a}\cdot\vec{b} &= |a|\, |b|\cos\theta \\
&= a_1b_1^{*} + a_2b_2^{*}+ \cdots+a_nb_n^{*}
\end{align}
特に、
$$\vec{a}\cdot\vec{b} =0 \ \Leftrightarrow \ \vec{a} \perp \vec{b}$$
3. 連続関数 f(x), g(x) の内積
連続関数 $f(x), g(x)$ の内積は、
$$\int^{\infty}_{-\infty}f(x)\ g(x)^{*}\ dx$$
4. 正規直交基底
基底のとり方のうち、”大きさが1” かつ ”互いに直交”しているものを正規直交基底という
例)デカルト座標系
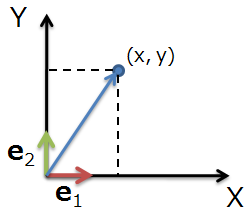
(https://imagingsolution.net/math/orthonormal_basis/ )
上図では、
e_1 =
\left(
\begin{array}{c}
1 \\
0 \\
\end{array}
\right),\ \ e_2 =
\left(
\begin{array}{c}
0 \\
1 \\
\end{array}
\right)
が正規直交基底ベクトルである.
5. 正規直交基底に対する基底変換
$$\vec{r} = c_1 \vec{e_1} + c_2 \vec{e_2}$$
において、”重み付け” $c_1, c_2$ は、
$$\vec{r}\cdot\vec{e_1}=c_1\ \vec{e_1}\cdot\vec{e_1}+c_2\ \vec{e_2}\cdot\vec{e_1} = c_1$$$$\vec{r}\cdot\vec{e_2}=c_1\ \vec{e_1}\cdot\vec{e_2}+c_2\ \vec{e_2}\cdot\vec{e_2} = c_2$$
で求められる.
フーリエ変換とは?
一般の関数 $f(t)$ について、$f(t)$ を、
$$”重み付け”をF(\omega)、基底を\frac{1}{\sqrt{2\pi}}e^{i\omega t}$$
の無限次元の線型結合として表すと、$$f(t)=\int^{\infty}_{-\infty}F(\omega)\left(\frac{1}{\sqrt{2\pi}}e^{i\omega t}\right)^{*} d\omega$$と表せる.
この”重み付け”$F(\omega)$を求める操作のことをフーリエ変換という.
ここで、上記の 5. 正規直交基底に対する基底変換 を利用すると、
$F(\omega)$(重み付け)を求めるには、$f(t)$と基底の内積をとれば良いので、
\begin{align}
F(\omega) = \int^{\infty}_{-\infty}f(t)\left(\frac{1}{\sqrt{2\pi}}e^{i\omega t}\right)^{*} dt
\end{align}
これをフーリエ変換という.
まとめ
$$フーリエ変換: F(\omega) = \int^{\infty}_{-\infty}f(t)\left(\frac{1}{\sqrt{2\pi}}e^{i\omega t}\right)^{*} dt$$
$$逆フーリエ変換: f(t) = \int^{\infty}_{-\infty}F(\omega)\left(\frac{1}{\sqrt{2\pi}}e^{i\omega t}\right) d\omega$$