非自明な関数の最大値、または最小値を求める手法は Black-Box最適化 と呼ばれます。Black-Box最適化の中でもベイズの枠組みを用いて、関数の最大値、または最小値を求めていく方法を、 ベイズ最適化(Bayesian Optimization) と呼びます。
目的関数の符号を逆転させることで最大値を求めることと最小値を求めることは等価になるので、以下の記事では関数の最大値についてのみ議論を行います。
一般的なベイズ最適化は、連続値を持つ関数に用いられ、その関数の最大値を ランダムサーチ(Random Search) などと比べ効率的に見つけ出すことができます。
一方で、一般的なベイズ最適化を組み合わせ最適化問題に用いる場合には、探索点が重複してしまうなどの問題が発生してしまいます。
この記事では Bayesian Optimization of Combinatorial Structures(BOCS) というアルゴリズムを原論文を引用する形で紹介します。
イントロダクション
ベイズ最適化は、$f(x)$の具体的な形がわからないが、$f(x)$の最大値を求めたいときに用いられる手法です。一般的には、一回の評価(機械学習的に表現すると一回の学習)に計算コストがかかる関数の最大値を求める場合などに用いられます。
ベイズ最適化では、評価に大きな計算コストのかかる目的関数$f(x)$の代わりに 代理関数(Surrogate function) を用いて、次の探索点を求めます。このとき、次の探索点を決める関数を 獲得関数(Acquisition function) と呼びます。
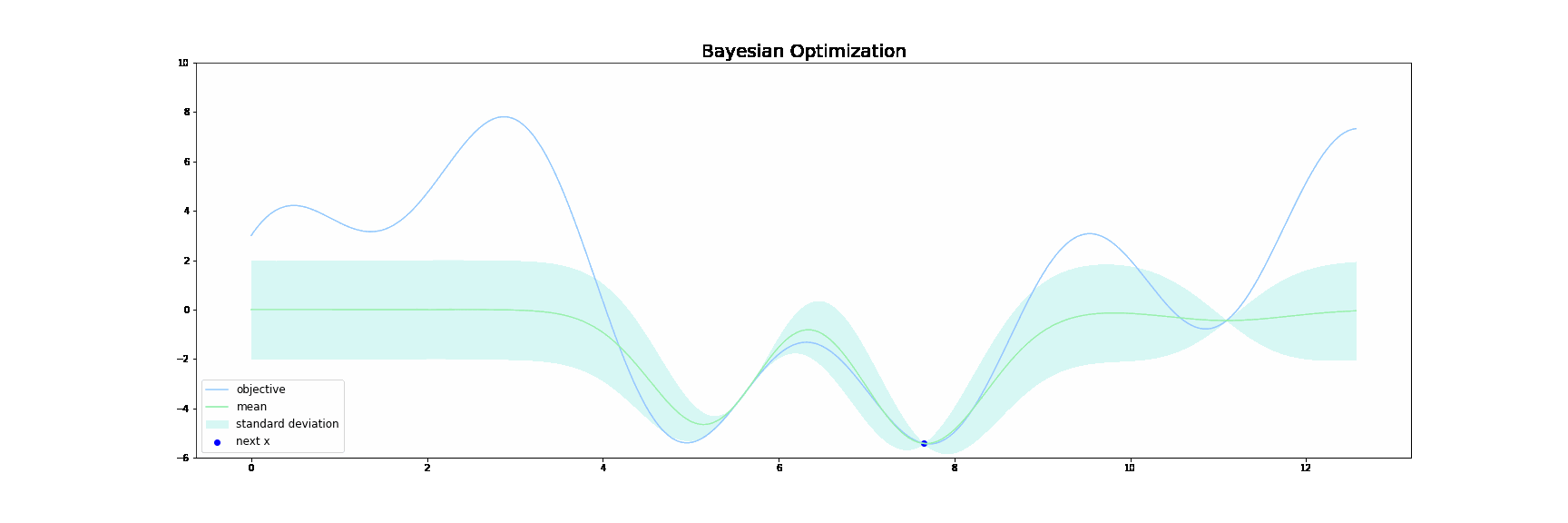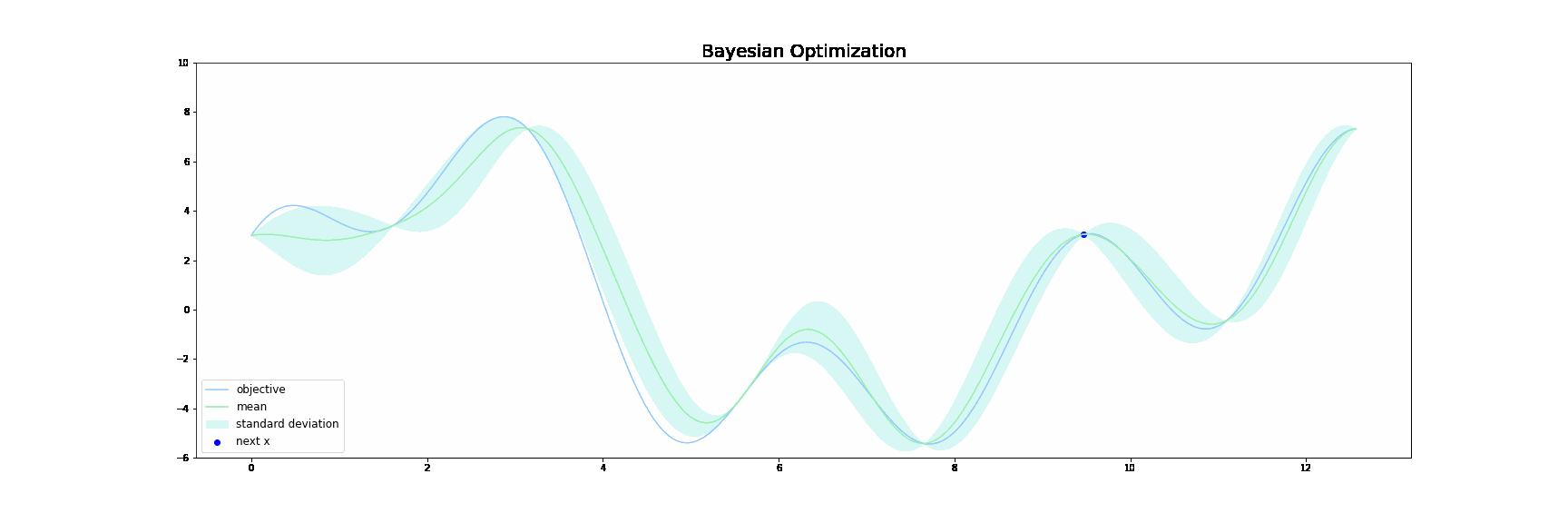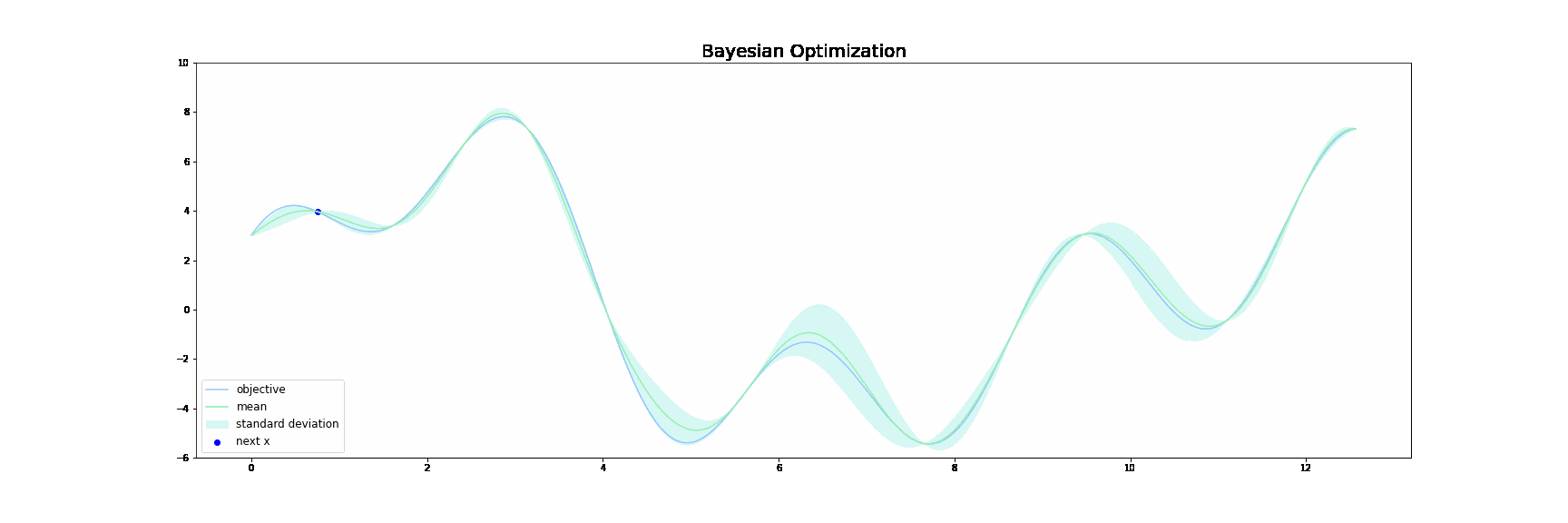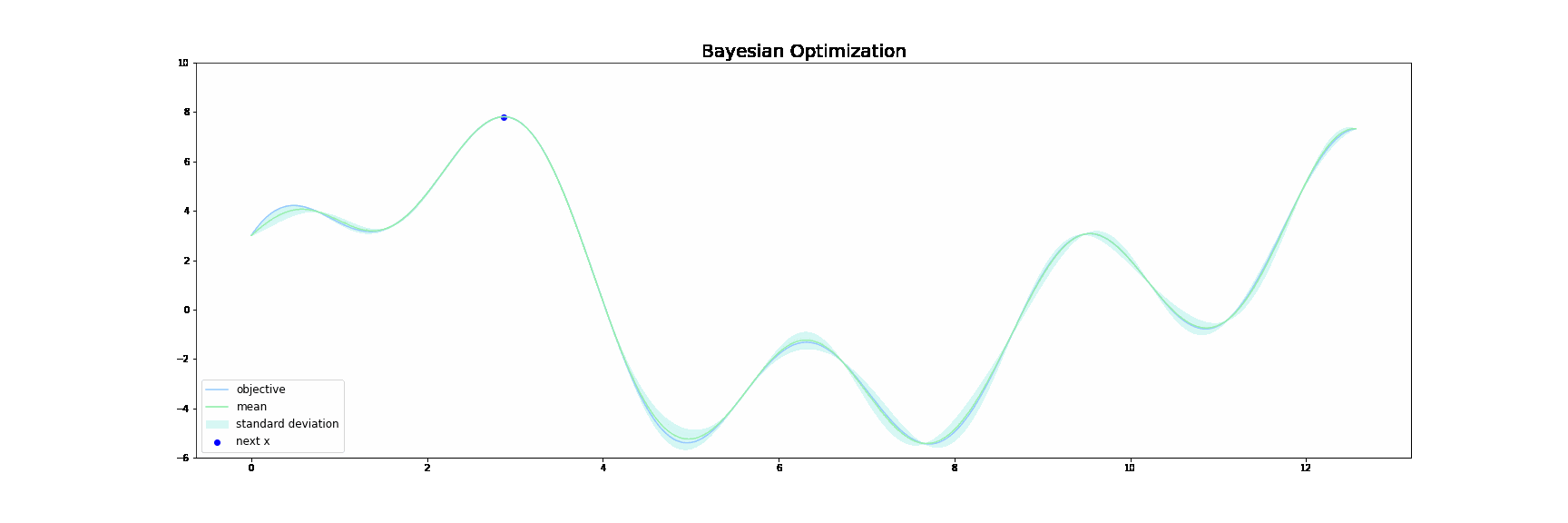
下図はベイズ最適化が行われる様子をgifで表したものです。青線が目的関数$f(x)$で、緑線は 代理関数(Surrogate function) の出力になります。緑色の領域は全体の95%の信頼区間を表しています。
ベイズ最適化は以下の操作を繰り返すことで探索を行います。
- 事前に目的関数$f(x)$からいくつかのサンプルをサンプリングしておく
- 保持しているサンプルを用いて代理関数を計算する
- 代理関数の出力を用いて獲得関数を計算し次の探索点を決める
- 目的関数$f(x)$から獲得関数で決めた探索点をサンプリングする
- 新しいサンプルに既存のサンプルを追加する
- 2~5を繰り返す
ざっくりと概説すると、サンプル数が増えるにつれて、代理関数がうまく目的関数$f(x)$を近似していき、最終的に代理関数を最大にする点が目的関数$f(x)$も最大にする点となるという仕組みです。
以前に一般的なベイズ最適化についてもまとめているので、必要に応じて参照してください。
組み合わせ構造に対するベイズ最適化
Black-Box最適化は最大値を発見したい関数の具体的な形状がわかっていない状況で用いられます。
組み合わせ構造に対するベイズ最適化の文脈で私たちが知り得る情報は、目的関数に何個の変数があるか、関数に入力を入れるとどんな値が返ってくるか、関数が組み合わせ構造を持っている、という3点です。
例えば、10個の変数 $x_1, x_2, \dots, x_{10}$ を持つBlack-Box関数の最大値を見つけたいとしましょう。
関数は組み合わせ構造を持っているので、入力は0と1で構成されるベクトルになります。
\mathbf{x}=(x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9, x_{10})=(0,0,0,1,0,0,0,1,0,0)
また、「関数に入力を入れるとどんな値が返ってくるか」も知ることができるので、ランダムに生成したベクトル $\mathbf{x}$ を入力することでサンプルデータを集めることもできます。
D={(\mathbf{x}_1,y_1), (\mathbf{x}_2,y_2), \dots, (\mathbf{x}_{n},y_{n})}
これらの情報からベイズ最適化の枠組みを用いて関数の最大値を見つけにいきます。
一般的なベイズ最適化では、代理関数には ガウス過程(Gaussian Process) などを、獲得関数には 期待改善度(Expected Improvement) などを用います。
これに対し、BOCSでは代理関数には スパース性を導入したベイズ線形回帰(Sparse Bayesian Linear Regression) を、獲得関数には シミュレーテッド・アニーリング(Simulated Annealing) を用います。
詳細は後述しますが、2つの変更に共通するのは組合せ最適化の解はスパースである傾向にあるということを上手くベイズ最適化に組み込んだという点です。
| BO | BOCS | |
|---|---|---|
| 代理関数 | ガウス過程など | スパース性を導入したベイズ線形回帰 |
| 獲得関数 | UCB, PI, EIなど | シミュレーテッド・アニーリングなど |
代理関数(Surrogate Function)
連続値を出力にもつ関数 $f(x)$ を最適化する場合は、代理関数には ガウス回帰(Gaussian Process Regression) が用いるのが一般的です。ただ、必ずしもガウス過程を用いる必要はなく、 ランダムフォレスト(Random Forest) などのアルゴリズムも代理関数として採用されることもあります。
どんなN個の入力の集合 $(\mathbf{x_{1}},\mathbf{x_{2}},\dots,\mathbf{x_{N}})$ についても、対応する出力 $(f(\mathbf{x_{1}}),f(\mathbf{x_{2}}),\dots,f(\mathbf{x_{N}}))$ の同時分布 $p(\mathbf{f})$ が、平均 $\mathbf{u}$ と $K_{n{n'}}=k(\mathbf{x_n},\mathbf{x_{n'}})$ を要素とする共分散行列 $\mathbf{K}$ のガウス分布 $\mathbb{N}(\mathbf{u},\mathbf{K})$ に従うとき、 $\mathbf{f}$ は ガウス過程(Gaussian Process) に従うと言います。
\mathbf{f}\sim \textrm{GP}(\mathbf{u},k(\mathbf{x},\mathbf{x'}))
代理関数にガウス過程を用いるとき、入力に対する出力がガウス分布に従うという仮定をおいていますが、組み合わせ構造をもつ関数に対する仮定としてはやや強すぎる仮定であると言えます。実際に組み合わせ最適化において、ガウス過程を代理関数として用いてベイズ最適化を実行しても、あまり良い結果は得られません。
BOCSではガウス過程の代わりにスパース性を導入したベイズ線形回帰を代理関数に用います。
変数 $x_1, x_2, \dots, x_{10}$ について、2つの変数の組み合わせまでが関数の出力に影響するという仮定を置いて線形回帰を行います。
y = \beta_0 + \beta_1 x_{1} + \cdots +\beta_{10} x_{10} + \beta_{(1,2)} x_{1} x_{2} + \dots + \beta_{(9,10)} x_{9} x_{10}
回帰係数の数は $1 + 10 + {}_{10} C_2 = 56$ 個になります。変数の数が $n$ 個のときは、 $1 + n + {}_n C_2$ 個です。
変数 $x_1, x_2, \dots, x_{10}$ から $k$ 個の変数の組み合わせを生成するプログラムを実装します。
def _order_effects(order: np.int64, X: np.ndarray) -> np.ndarray:
n_samples, n_vars = X.shape
X_allpairs = X.copy()
for i in range(2, order + 1, 1):
# generate all combinations of indices (without diagonals)
offdProd = np.array(list(combinations(np.arange(n_vars), i)))
# generate products of input variables
x_comb = np.zeros((n_samples, offdProd.shape[0], i))
for j in range(i):
x_comb[:, :, j] = X[:, offdProd[:, j]]
X_allpairs = np.append(X_allpairs, np.prod(x_comb, axis=2), axis=1)
return X_allpairs
プログラムにおいて $order$ に3以上の値を代入することで、3つ以上の変数の組み合わせまで考慮することもできますが、変数の数が増えるにつれて急激に回帰係数の数が増えてしまうため、2つまでの変数の組み合わせを考慮するのが一般的な問題に対しては良いようです。詳しくは原論文を参照してください。
組合せ最適化の解はスパースになる傾向があるという事前知識をモデルに組み込むため、回帰係数 $\boldsymbol \beta$ の事前分布に馬蹄分布を設定します。馬蹄分布は次のような数式で記述されます。
\beta_i|\lambda_i,\tau\sim\mathbb{N}(0,\lambda_i^2\tau^2)
\lambda_i\sim C^+(0,1)
$C^+(0,1)$ は半コーシー分布です。半コーシー分布は次のような数式で記述されます。馬蹄分布は、$\lambda_i$ が半コーシー分布から生成されているとき、平均 $0$ で分散 $\lambda_i^2\tau^2$ のガウス分布から生成されます。
\begin{split} \begin{align}
f(x;a, b) = \left\{\begin{array}{cll}
\frac{2}{\pi b}\,\frac{1}{1 + (x-a)^2/b^2} & & x \ge a \\[1em]
0 & & \text{otherwise}.
\end{array}\right.
\end{align}\end{split}
馬蹄分布やスパース性を導入した線形回帰についての記事も以前執筆したので、必要に応じて参照していただければと思います。
ベイズ線形回帰の出力に対して、
y = \beta_0 + \beta_1 x_{1} + \cdots +\beta_{10} x_{10} + \beta_{(1,2)} x_{1} x_{2} + \dots + \beta_{(9,10)} x_{9} x_{10}
ガウス分布 $\mathbb{N}(0, \sigma^2)$ に従ったノイズ $\epsilon$ がのったものが観測されるとすると、
\mathbf{y}=\mathbf{X}\boldsymbol \beta + \boldsymbol \epsilon
\boldsymbol \epsilon\sim\mathbb{N}(\mathbf{0},\sigma^2\mathbf{I})
\beta_i|\lambda_i^2,\tau^2,\sigma^2\sim\mathbb{N}(0,\lambda_i^2\tau^2\sigma^2)
と表現することができます。
このとき $\boldsymbol \beta$ の事後分布は次のような条件付き分布として計算することができます。詳細な導出は省略します。気になる人はこの論文を参照してください。
\boldsymbol \beta|\cdot\sim\mathbb{N}(\mathbf{A}^{-1}\mathbf{X}^{\top}\mathbf{y},\sigma^2\mathbf{A}^{-1}),\quad \mathbf{A}=(\mathbf{X}^{\top}\mathbf{X}^{-1}+\mathbf{\Lambda_{*}}^{-1}),\quad \mathbf{\Lambda_{*}}=\tau^2\mathbf{\Lambda}
\mathbf{\Lambda}=\textrm{diag}(\lambda_1^2,\dots,\lambda_p^2)
同様に $\sigma^2,\lambda_i^2,\tau^2$ の条件付き事後分布も次のように計算することができます。
\sigma^2|\cdot\sim\textrm{IG}(\frac{(n+p)}{2},\frac{(\mathbf{y}-\mathbf{X}\boldsymbol\beta)^{\top}(\mathbf{y}-\mathbf{X}\boldsymbol\beta)}{2} + \frac{\boldsymbol\beta^{\top}\mathbf{\Lambda_{*}^{-1}\boldsymbol\beta}}{2})
\lambda_i^2|\cdot\sim\textrm{IG}(1,\frac{1}{\nu_i}+\frac{\beta_i^2}{2\tau^2\sigma^2})
\tau_i^2|\cdot\sim\textrm{IG}(\frac{p+1}{2},\frac{1}{\xi}+\frac{1}{2\sigma^2}\sum_{i=1}^p \frac{\beta_i^2}{\lambda_i^2})
上記の条件付き事後分布には、元々はなかった補助変数 $\nu_i,\xi$ が使われています。これらの事後分布は次のように求められます。
\nu_i|\cdot\sim\textrm{IG}(1,1+\frac{1}{\lambda_i^2})
\xi|\cdot\sim\textrm{IG}(1,1+\frac{1}{\tau^2})
興味深いことに回帰係数以外の全てのパラメータは逆ガンマ分布の形で記述することができました。条件付き事後分布を導出できたので ギブス・サンプリング(Gibbs Sampling) を用いて回帰係数をサンプリングすることができます。
データ $(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2), \dots, (\mathbf{x}_n,y_n)$ から回帰係数をサンプリングするプログラムを実装します。
def _bhs(X: np.ndarray, y: np.ndarray, n_samples: np.int64 = 1,
burnin: np.int64 = 200) -> Union[np.ndarray, np.float64]:
n, p = X.shape
XtX = X.T @ X
beta = np.zeros((p, n_samples))
beta0 = np.mean(y)
sigma2 = 1
lambda2 = np.random.uniform(size=p)
tau2 = 1
nu = np.ones(p)
xi = 1
# Run Gibbs Sampler
for i in range(n_samples + burnin):
Lambda_star = tau2 * np.diag(lambda2)
A = XtX + np.linalg.inv(Lambda_star)
A_inv = np.linalg.inv(A)
b = np.random.multivariate_normal(A_inv @ X.T @ y, sigma2 * A_inv)
# Sample sigma^2
e = y - np.dot(X, b)
shape = (n + p) / 2.
scale = np.dot(e.T, e) / 2. + np.sum(b**2 / lambda2) / tau2 / 2.
sigma2 = 1. / self.rs.gamma(shape, 1. / scale)
# Sample lambda^2
scale = 1. / nu + b**2. / 2. / tau2 / sigma2
lambda2 = 1. / np.random.exponential(1. / scale)
# Sample tau^2
shape = (p + 1.) / 2.
scale = 1. / xi + np.sum(b**2. / lambda2) / 2. / sigma2
tau2 = 1. / np.random.gamma(shape, 1. / scale)
# Sample nu
scale = 1. + 1. / lambda2
nu = 1. / np.random.exponential(1. / scale)
# Sample xi
scale = 1. + 1. / tau2
xi = 1. / np.random.exponential(1. / scale)
if i >= burnin:
beta[:, i - burnin] = b
return beta, beta0
回帰係数における切片に対応する項 $\beta_0$ は、入力が $\mathbf{0}$ だったときの $y$ なのでデータの $\mathbf{y}$ の平均として計算することができます。
$\beta_0$ 以外の係数 $\beta_1,\beta_2,\dots,\beta_{(1,2)},\dots\beta_{(9,10)}$ の推定には、解析的に導出した条件付き事後分布を用いてギブス・サンプリングによりサンプリングを行なっています。
また、 マルコフ連鎖モンテカルロ法(Markov chain Monte Calro) 法を用いる慣例として、最初の200個のサンプルは 焼き入れ(burn-in) として棄却しています。
最後にスパース性を導入したベイズ線形回帰を1つのクラスにまとめて、つかいやすいようにします。
class SparseBayesianLinearRegression:
def __init__(self, n_vars: np.int64, order: np.int64, random_state: np.int64 = 42):
assert n_vars > 0, "The number of variables must be greater than 0"
self.n_vars = n_vars
self.order = order
self.rs = np.random.RandomState(random_state)
self.n_coef = int(1 + n_vars + 0.5 * n_vars * (n_vars - 1))
self.coefs = self.rs.normal(0, 1, size=self.n_coef)
def fit(self, X: np.ndarray, y: np.ndarray):
"""Fit Sparse Bayesian Linear Regression
Args:
X (np.ndarray): matrix of shape (n_samples, n_vars)
y (np.ndarray): matrix of shape (n_samples, )
"""
assert X.shape[1] == self.n_vars, "The number of variables does not match. X has {} variables, but n_vars is {}.".format(
X.shape[1], self.n_vars)
assert y.ndim == 1, "y should be 1 dimension of shape (n_samples, ), but is {}".format(
y.ndim)
# x_1, x_2, ... , x_n
# ↓
# x_1, x_2, ... , x_n, x_1*x_2, x_1*x_3, ... , x_n * x_ n-1
X = self._order_effects(X)
needs_sample = 1
while (needs_sample):
try:
_coefs, _coef0 = self._bhs(X, y)
except Exception as e:
print(e)
continue
if not np.isnan(_coefs).any():
needs_sample = 0
self.coefs = np.append(_coef0, _coefs)
def predict(self, x: np.ndarray) -> np.float64:
assert x.shape[1] == self.n_vars, "The number of variables does not match. x has {} variables, but n_vars is {}.".format(
x.shape[1], self.n_vars)
x = self._order_effects(x)
x = np.append(1, x)
return x @ self.coefs
def _order_effects(self, X: np.ndarray) -> np.ndarray:
"""Compute order effects
Computes data matrix for all coupling
orders to be added into linear regression model.
Order is the number of combinations that needs to be taken into consideration,
usually set to 2.
Args:
X (np.ndarray): input materix of shape (n_samples, n_vars)
Returns:
X_allpairs (np.ndarray): all combinations of variables up to consider,
which shape is (n_samples, Σ[i=1, order] comb(n_vars, i))
"""
assert X.shape[1] == self.n_vars, "The number of variables does not match. X has {} variables, but n_vars is {}.".format(
X.shape[1], self.n_vars)
n_samples, n_vars = X.shape
X_allpairs = X.copy()
for i in range(2, self.order + 1, 1):
# generate all combinations of indices (without diagonals)
offdProd = np.array(list(combinations(np.arange(n_vars), i)))
# generate products of input variables
x_comb = np.zeros((n_samples, offdProd.shape[0], i))
for j in range(i):
x_comb[:, :, j] = X[:, offdProd[:, j]]
X_allpairs = np.append(X_allpairs, np.prod(x_comb, axis=2), axis=1)
return X_allpairs
def _bhs(self, X: np.ndarray, y: np.ndarray, n_samples: np.int64 = 1,
burnin: np.int64 = 200) -> Union[np.ndarray, np.float64]:
"""Run Bayesian Horseshoe Sampler
Sample coefficients from conditonal posterior using Gibbs Sampler
<Reference>
A simple sampler for the horseshoe estimator
https://arxiv.org/pdf/1508.03884.pdf
Args:
X (np.ndarray): input materix of shape (n_samples, 1 + Σ[i=1, order] comb(n_vars, i)).
y (np.ndarray): matrix of shape (n_samples, ).
n_samples (np.int64, optional): The number of sample. Defaults to 1.
burnin (np.int64, optional): The number of sample to be discarded. Defaults to 200.
Returns:
Union[np.ndarray, np.float64]: Coefficients for Linear Regression.
"""
assert X.shape[1] == self.n_coef - 1, "The number of combinations is wrong, it should be {}".format(
self.n_coef)
assert y.ndim == 1, "y should be 1 dimension of shape (n_samples, ), but is {}".format(
y.ndim)
n, p = X.shape
XtX = X.T @ X
beta = np.zeros((p, n_samples))
beta0 = np.mean(y)
sigma2 = 1
lambda2 = self.rs.uniform(size=p)
tau2 = 1
nu = np.ones(p)
xi = 1
# Run Gibbs Sampler
for i in range(n_samples + burnin):
Lambda_star = tau2 * np.diag(lambda2)
A = XtX + np.linalg.inv(Lambda_star)
A_inv = np.linalg.inv(A)
b = self.rs.multivariate_normal(A_inv @ X.T @ y, sigma2 * A_inv)
# Sample sigma^2
e = y - np.dot(X, b)
shape = (n + p) / 2.
scale = np.dot(e.T, e) / 2. + np.sum(b**2 / lambda2) / tau2 / 2.
sigma2 = 1. / self.rs.gamma(shape, 1. / scale)
# Sample lambda^2
scale = 1. / nu + b**2. / 2. / tau2 / sigma2
lambda2 = 1. / self.rs.exponential(1. / scale)
# Sample tau^2
shape = (p + 1.) / 2.
scale = 1. / xi + np.sum(b**2. / lambda2) / 2. / sigma2
tau2 = 1. / self.rs.gamma(shape, 1. / scale)
# Sample nu
scale = 1. + 1. / lambda2
nu = 1. / self.rs.exponential(1. / scale)
# Sample xi
scale = 1. + 1. / tau2
xi = 1. / self.rs.exponential(1. / scale)
if i >= burnin:
beta[:, i - burnin] = b
return beta, beta0
獲得関数
獲得関数は代理関数の出力に基づき次の探索点を決める関数です。
$n$ 個のデータ $\mathcal{D}_n$ から代理関数を作り、獲得関数$a(x;\mathcal{D}_n)$を用いて
\newcommand{\argmax}{\mathop{\rm arg~max}\limits}
x_{n+1}=\argmax_x a(x;\mathcal{D}_n)
とすることで、次の探索点を定めます。
一般的なベイズ最適化では期待改善度などが用いられますが、組み合わせ構造に対するベイズ最適化では シミュレーテッド・アニーリング を用います。
シミュレーテッド・アニーリングは「焼きなまし法」とも呼ばれ、広大な探索空間内の与えられた関数の大域的最適解を近似するアルゴリズムの一つです。「焼きなまし」の名称から察せられる通り、金属を高温の状態にして、徐々に温度を下げることで秩序がある構造を作り出す焼きなましの技術をコンピュータ上で再現したアルゴリズムになります。
一般的なベイズ最適化で用いられる獲得関数は、変数の数が多くなるにつれて獲得関数が平になってしまい、次の探索点を決めづらくなるといった問題があります。
組み合わせ構造に対するベイズ最適化では、変数の数が10個のときですら56個の係数が必要になるので、シミュレーテッド・アニーリングなどの広大な探索空間内の大域的最適解を探しに行けるアルゴリズムが獲得関数に適していると言えます。
この記事では触れませんが、シミュレーテッド・アニーリングの他にも 半正定値計画緩和(semi-definite programming relaxation) を用いる方法も論文で紹介されています。
SA法では以下のような手順で探索を行なっていきます。
- 初期温度を設定する
- 初期値をサンプリングする
- 温度を下げる
- ランダムに次の点をサンプリングする
4.1. ランダムにサンプルした点が現在の点よりも良かったら、現在の点を更新する
4.2. ランダムにサンプルした点が現在の点よりも悪くても、温度に依存する一定確率で現在の点を更新する - 3~4を繰り返す
3の温度を下げる方法は、たとえば次のような関数が使われます。
T = 1.
cooling_rate = 0.9
def cool(T): return cooling_rate * T
T = cool(T)
シミュレーテッド・アニーリングに関する記事も以前執筆したので、必要に応じて参照していただければと思います。
シミュレーテッド・アニーリングはアルゴリズムとしては単純なので、実装もそこまで難しくありません。
def simulated_annealinng(objective, n_vars: np.int64, cooling_rate: np.float64 = 0.985,
n_iter: np.int64 = 100) -> Union[np.ndarray, np.ndarray]:
X = np.zeros((n_iter, n_vars))
obj = np.zeros((n_iter, ))
# set initial temperature and cooling schedule
T = 1.
def cool(T): return cooling_rate * T
curr_x = sample_binary_matrix(1, n_vars)
curr_obj = objective(curr_x)
best_x = curr_x
best_obj = curr_obj
for i in range(n_iter):
# decrease T according to cooling schedule
T = cool(T)
new_x = sample_binary_matrix(1, n_vars)
new_obj = objective(new_x)
# update current solution
if (new_obj > curr_obj) or (rs.rand()
< np.exp((new_obj - curr_obj) / T)):
curr_x = new_x
curr_obj = new_obj
# Update best solution
if new_obj > best_obj:
best_x = new_x
best_obj = new_obj
# save solution
X[i, :] = best_x
obj[i] = best_obj
return X, obj
BOCSの実装
ベイズ最適化のフローは次のようになります。
- 事前に目的関数$f(x)$からいくつかのサンプルをサンプリングしておく
- 保持しているサンプルを用いて代理関数を計算する
- 代理関数の出力を用いて獲得関数を計算し次の探索点を決める
- 目的関数$f(x)$から獲得関数で決めた探索点をサンプリングする
- 新しいサンプルに既存のサンプルを追加する
- 2~5を繰り返す
組み合わせ構造に対するベイズ最適化も同様のフローで、代理関数と獲得関数に工夫を施しただけです。
def sample_binary_matrix(n_samples: np.int64, n_vars: np.int64) -> np.ndarray:
"""Sample binary matrix
Args:
n_samples (np.int64): The number of samples.
n_vars (np.int64): The number of variables.
Returns:
np.ndarray: Binary matrix of shape (n_samples, n_vars)
"""
# Generate matrix of zeros with ones along diagonals
sample = np.zeros((n_samples, n_vars))
# Sample model indices
sample_num = rs.randint(2**n_vars, size=n_samples)
strformat = '{0:0' + str(n_vars) + 'b}'
# Construct each binary model vector
for i in range(n_samples):
model = strformat.format(sample_num[i])
sample[i, :] = np.array([int(b) for b in model])
return sample
def bocs_sa(objective, n_vars: np.int64, n_init: np.int64 = 10, n_trial: np.int64 = 100, sa_reruns: np.int64 = 5):
# Set the number of Simulated Annealing reruns
sa_reruns = 5
# Initial samples
X = sample_binary_matrix(n_init, n_vars)
y = objective(X)
# Define surrogate model
sblr = SparseBayesianLinearRegression(n_vars, 2)
sblr.fit(X, y)
for _ in range(n_trial):
def surrogate_model(x): return sblr.predict(x)
sa_X = np.zeros((sa_reruns, n_vars))
sa_y = np.zeros(sa_reruns)
for j in range(sa_reruns):
opt_X, opt_y = simulated_annealinng(surrogate_model, n_vars)
sa_X[j, :] = opt_X[-1, :]
sa_y[j] = opt_y[-1]
max_idx = np.argmax(sa_y)
x_new = sa_X[max_idx, :]
# evaluate model objective at new evaluation point
x_new = x_new.reshape((1, 15))
y_new = objective(x_new)
# Update posterior
X = np.vstack((X, x_new))
y = np.hstack((y, y_new))
# Update surrogate model
sblr.fit(X, y)
return X, y
BOCSを用いて組み合わせ構造を持つ関数に対する最適化の実験を行なってみます。
目的関数を次のように設定します。(この目的関数は通常は私たちは見えないという意味でブラックボックスとなります。)
n_vars = 10
def quad_matrix(n_vars, alpha):
i = np.linspace(1, n_vars, n_vars)
j = np.linspace(1, n_vars, n_vars)
def K(s, t): return np.exp(-1 * (s - t)**2 / alpha)
decay = K(i[:, None], j[None, :])
Q = np.random.randn(n_vars, n_vars)
Q = Q * decay
return Q
Q = quad_matrix(n_vars, 10)
def objective(X: np.ndarray) -> np.float64:
return - np.diag(X @ Q @ X.T)
BOCSを用いて目的関数の最大値(目的関数にはマイナスをつけているので実際には最小値)を見つけてみます。
n_vars = 10
Q = quad_matrix(n_vars, 10)
def objective(X: np.ndarray) -> np.float64:
return - np.diag(X @ Q @ X.T)
# Run Bayesian Optimization
X, y = bocs_sa(objective, n_vars)
n_iter = np.arange(y.size)
bocs_opt = np.minimum.accumulate(y)
y_opt = np.min(objective(sample_binary_matrix(1000, n_vars)))
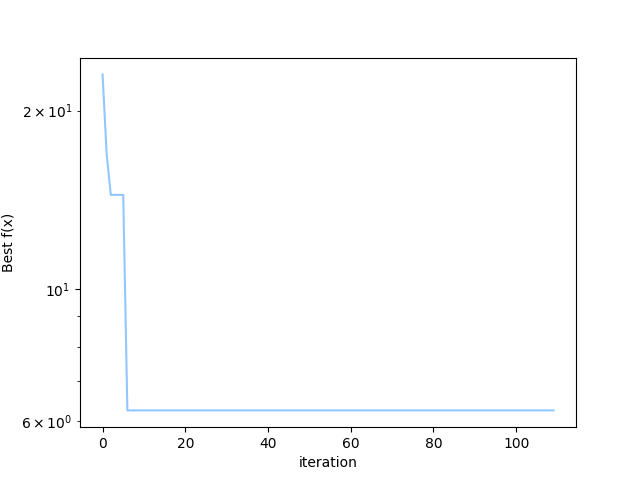
# Plot
fig = plt.figure()
plt.plot(n_iter, np.abs(bocs_opt - y_opt))
plt.yscale('log')
plt.xlabel('iteration')
plt.ylabel('Best f(x)')
fig.savefig('bocs_sa.png')
plt.close(fig)
最適解との差の絶対値がループを繰り返すにつれて0に近づいているので、アルゴリズムとして想定していた性能を発揮したと言えそうです。
まとめ
組み合わせ構造に対するベイズ最適化手法の解説を行いました。
一般的なベイズ最適化と異なる点としては、二つの変数までの組み合わせを考慮してスパース性を導入したベイズ線形回帰を代理関数とする点と、広大な探索空間の最適解の良い近似を与えるシミュレーテッドアニーリングを獲得関数に用いる点です。
今回の実験コードはGitHub上にあります。