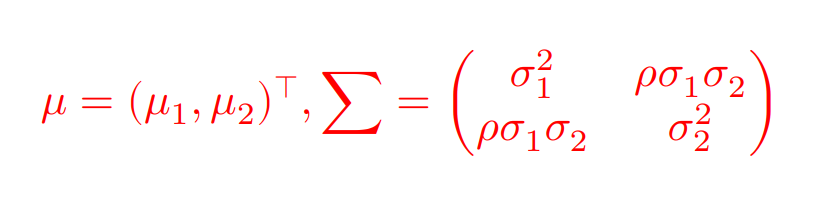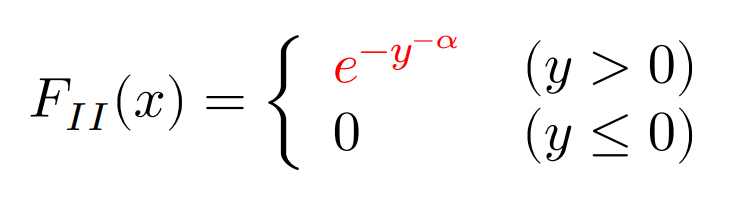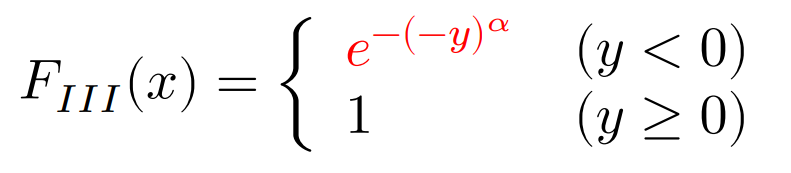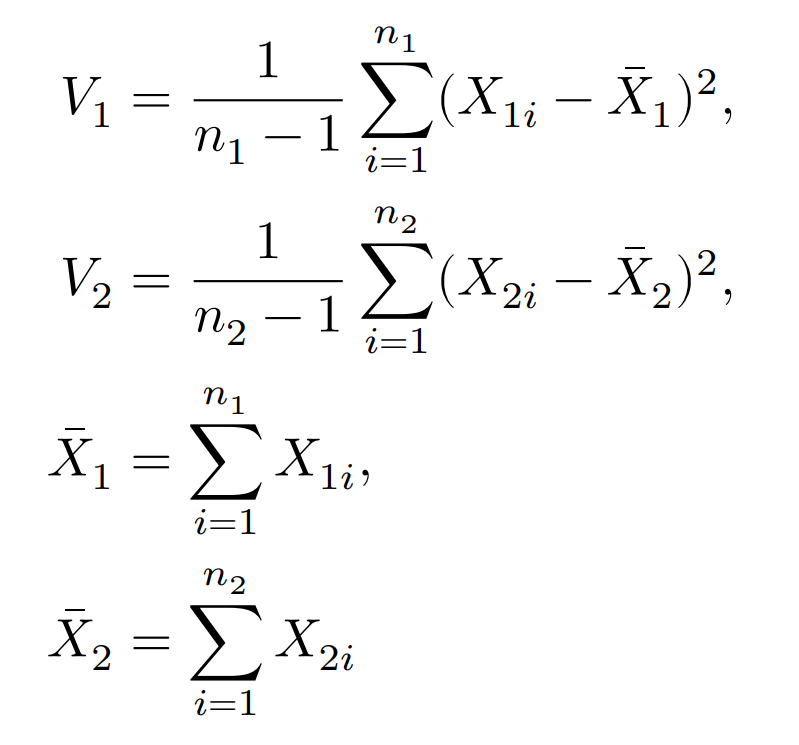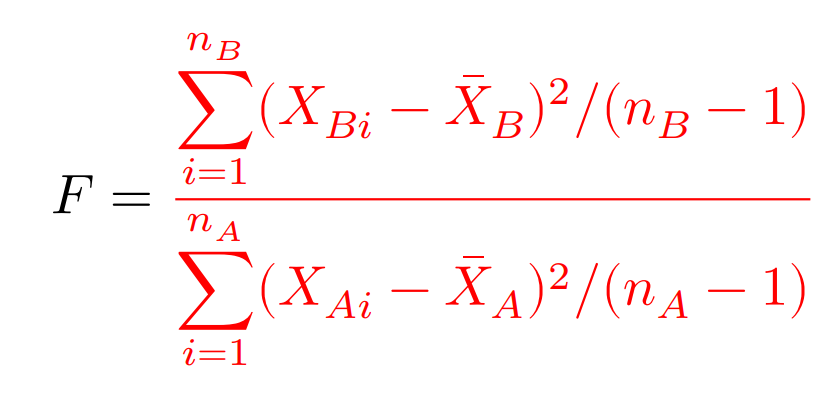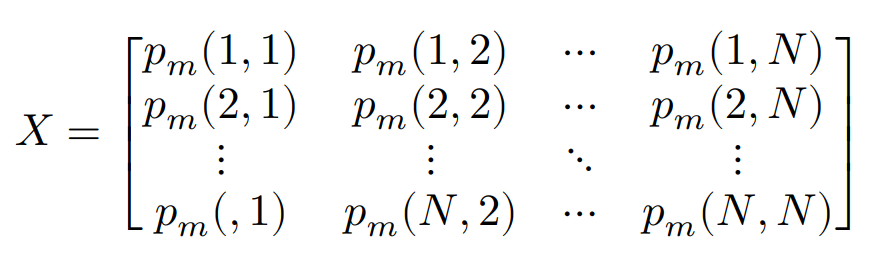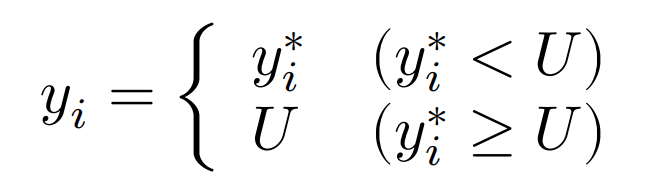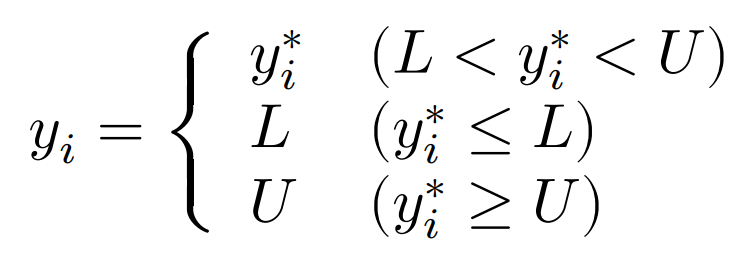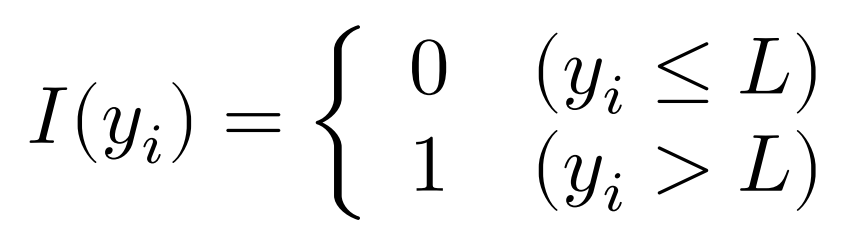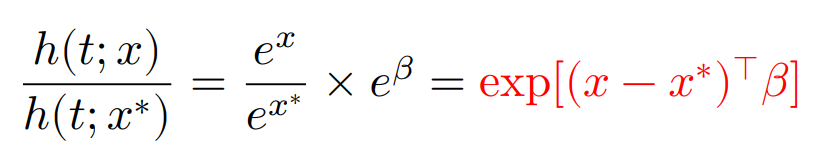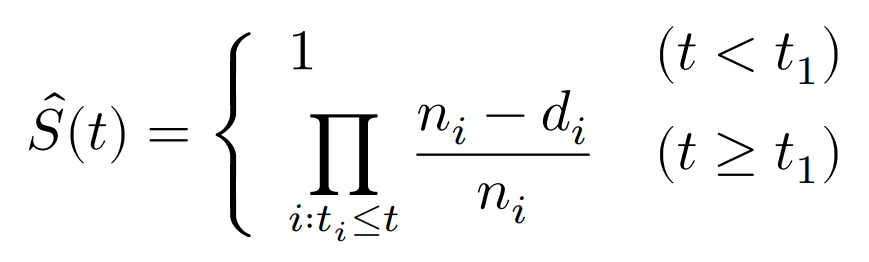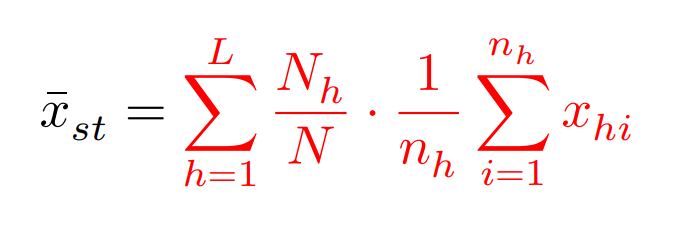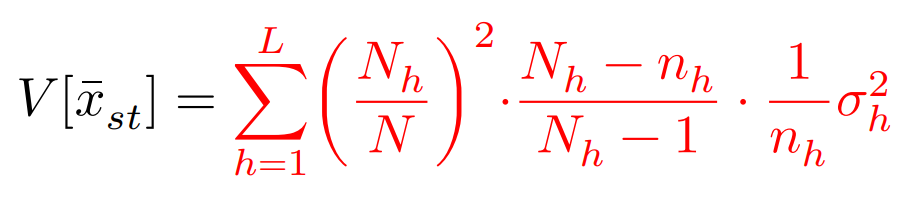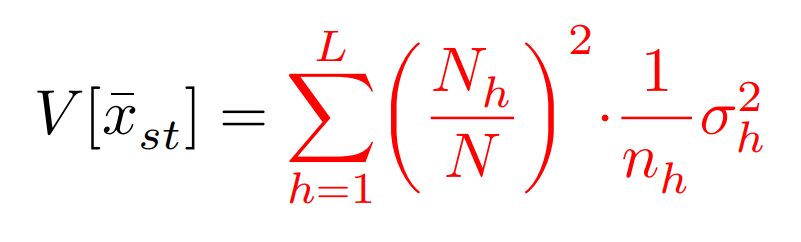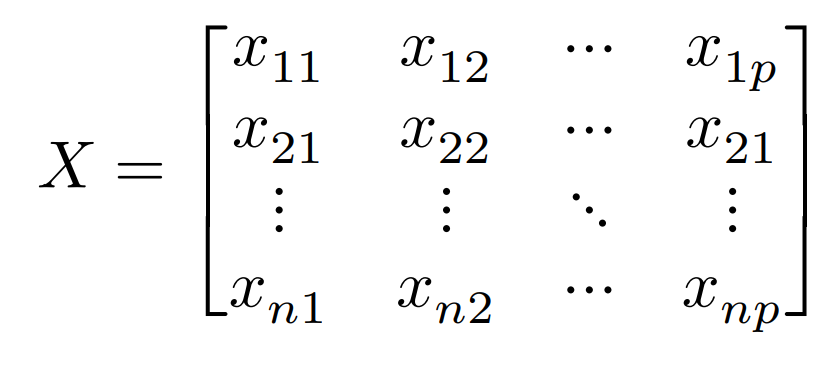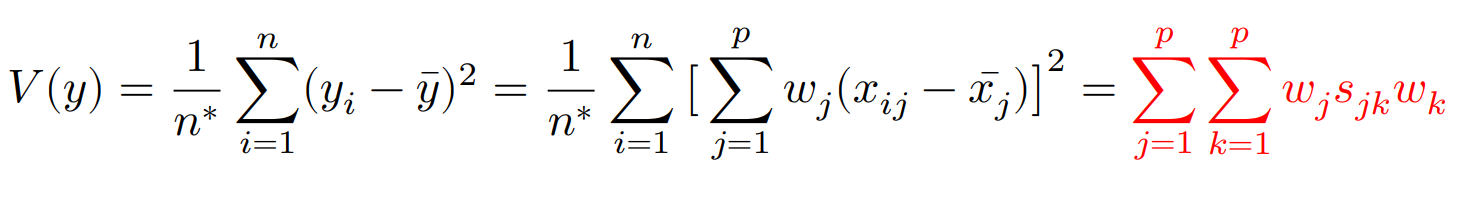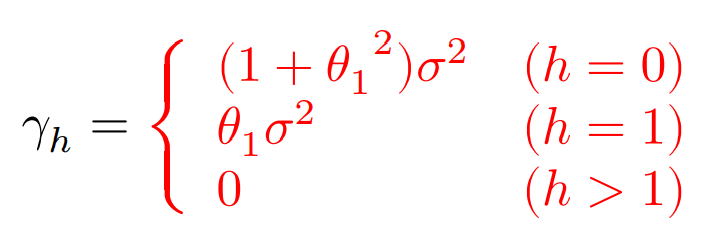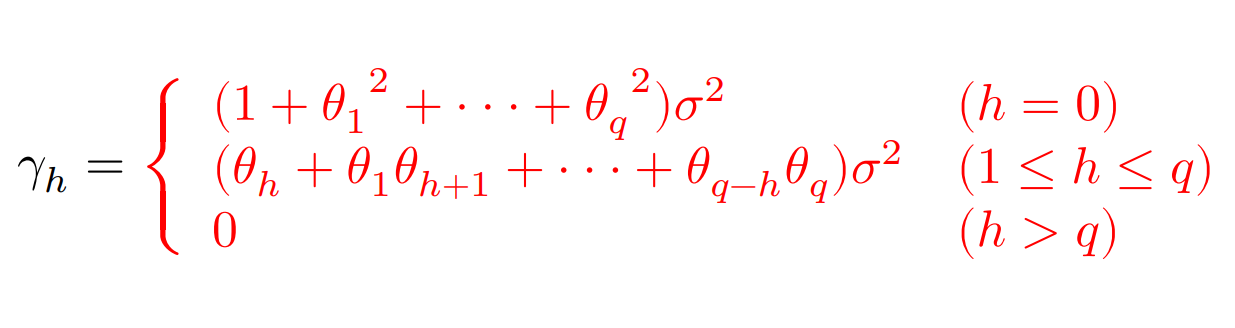統計学公式集

はじめに

この資料は,統計検定準１級までの範囲を一通り学習した人のためのものである。

導出や解説を省いて,問題を解くために必要な公式のみをまとめてある。

参考は「統計検定準１級対応　統計学実践ワークブック」(日本統計学会)

離散型分布,連続型分布,分散分析と実験計画法に関しては,表記の都合上別途まとめることとする。

なお,以下の議論において,厳密性は度外視している。

序章　２級の内容軽くまとめ

スタージェスの公式

データ数$n$に対するクラスの数$k$

$$
k=\color{red}{1+3.322 \log_{10} n}
$$

フィッシャーの３原則＆抽出法

〇フィッシャーの３原則

$$
\color{red}{\mbox{無作為化,繰り返し（反復）,局所管理}}
$$

〇抽出法

$\color{red}{\mbox{単純無作為抽出}}$

母集団から全ての個体が等しい確率で選ばれる。大きな母集団には適さない。

$\color{red}{\mbox{系統抽出（等間隔抽出）}}$

母集団の要素に番号を付け,等間隔に抽出する。散らばりは良いけど,集団に周期性があると精度は落ちる。

$\color{red}{\mbox{多段抽出}}$

大規模調査において,代表をいくつか抽出してからその中で細かく抽出する。「郡部や村ばかり抽出して,都会がないリスク」あり。段が増えるほど精度が落ちる。

$\color{red}{\mbox{集落（クラスター）抽出}}$

母集団から部分母集団（集落）を取り出す。そしてその要素を全て調べる。多段抽出と同じリスク・デメリット。

$\color{red}{\mbox{層別（層化）抽出}}$

集団を均質になるように分割。

ラスパイレス指数

$$
\mbox{ラスパイレス指数}=\color{red}{\frac{\sum P_t \cdot Q_0}{\sum P_0 \cdot Q_0}}
$$

$P_t$：比較年の価格,$P_0$：基準年の価格

$Q_t$：比較年の数量,$Q_0$：基準年の数量

第１章　事象と確率

I.ベイズの定理

まず,条件付確率を$P(B|A)=\color{red}{{\displaystyle\frac{P(A \cap B)}{P(A)}}}$と定義する。

ベイズの定理は,$\color{red}{P(A) \times P(B|A)=P(B) \times P(A|B)}$を用いて

$$
P(A|B)=\frac{P(B|A)P(A)}{P(B)}=\color{red}{\frac{P(B|A)P(A)}{P(B|A)P(A)+P(B|A^c)P(A^c)}}
$$

第２章　確率分布と母関数

I.累積分布関数と生存関数

確率変数$X$の累積分布関数を$F(x)=P(X \leq x)=\mbox{確率関数の和}$と定義する。

　　

生存関数

この時確率密度関数は$f(x)=F'(x)$とあらわされ,確率変数$X$が寿命を表す場合,

生存関数$\color{red}{S(x)=1-F(x)}$は時刻$x$においてまだ生きている確率を表す（時刻が進んでいくほど生きている確率は減っていく）。

寿命$X$を連続確率偏変数として,「時刻$x$において生存している者のうち,その後短時間に死亡する者の確率」であるハザード関数を

$$
h(x)=\color{red}{\frac{f(x)}{1-F(x)}}\color{black}{=}\color{red}{(-\log S(x))'}
$$
として定義できる。

II.同時確率密度関数

「$X$が値$x$をとり,$Y$が値$y$をとる確率」を$p(x,y)=P(X=x,Y=y)$で表し,その累積分布関数（$X \leq x$かつ$Y \leq y$）を,

$$
F(x,y)=P(X \leq x, Y \leq y)=\sum_{x' \leq x, y' \leq y} p(x', y')
$$
として定める。

$x$のみについて調べたい場合は,$y$について和をとることで,

$$
p_X(x)=\sum_y p(x,y)
$$
と考えればよい（周辺確率関数）。

また,$x$が定められたうえで$y$となる条件付確率関数は,

$$
p_{X|Y}(y|x)=\color{red}{\frac{p(x,y)}{p_X(x)}}
$$

連続確率関数の時,$X,Y$の同時確率密度関数は,

$$
f(x,y)=\frac{\partial^2}{\partial x \partial y}F(x,y)
$$

であり,長方形の領域の面積は

$$
P(x_1 \leq X \leq x_2, y_1 \leq Y \leq y_2)=\color{red}{\int_{x_1}^{x_2}\int_{y_1}^{y_2} f(x,y)dxdy}
$$

となり,$X$の周辺確率密度関数は$f_X(x)=\int_{-\infty}^\infty f(x,y)dy$で与えられる。

この時,$x$を所与としたときの$y$の条件付確率密度関数は,

$$
f_{X|Y}(y|x)=\color{red}{\frac{f(x,y)}{f_X(x)}}
$$

として,離散型と同様に表せる。

第３章　分布の特性値

I.歪度,尖度

歪度：${\displaystyle\color{red}{\frac{E[(X-E[X])^3]}{(V[X])^{3/2}}}}$

分布が左右対称であれば歪度は０
分布の裾が右に長ければ歪度は$\color{red}{\mbox{正}}$。左に長ければ$\color{red}{\mbox{負}}$

　　

尖度：${\displaystyle\color{red}{\frac{E[(X-E[X])^4]}{(V[X])^2}}}$

尖度は必ず０以上であり,正規分布の場合は$\color{red}{\mbox{３}}$

II.偏相関係数

$Z$の影響をのぞいた$X$と$Y$の偏相関係数は,

$$
\rho[X,Y|Z]=\color{red}{\frac{\rho[X,Y]-\rho[X,Z]\rho[Y,Z]}{\sqrt{(1-\rho[X,Z]^2)(1-\rho[Y,Z]^2)}}}
$$

$$\rho[X,Y]\mbox{ : XとYの相関係数}$$

III.変動係数

$$
\mbox{変動係数}=\color{red}{\frac{S_x}{\bar{x}}}\color{black}{=}\color{red}{\frac{\mbox{標準偏差}}{\mbox{平均}}}
$$

IV.様々な平均

〇刈り込み平均：外れ値をのぞく

順序データ$x_{(1)},x_{(2)},...,x_{(n)}$の両側$r$個をのぞいた平均値

$$
\color{red}{\frac{x_{(r+1)}+x_{(r+2)}+...+x_{(n-r-1)}+x_{(n-r)}}{n-2r}}
$$

〇正の値をとるデータの幾何平均:複利計算など

$x_1,...,x_n$が正のデータの時,幾何平均は

$$
\color{red}{Gx = (x_1*...*x_n)^{1/n}}
$$

〇調和平均:道のりの問題

$x_1,...,x_n$が正のデータの時,調和平均は

$$
\color{red}{H_x=\frac{n}{\sum_{i=1}^{n} 1/x_i}}
$$

〇荷重平均：重み付き平均

重み$w_1,...,w_n(w_i>0,w_1+...+w_n=1)$に対する$x_1,...,x_n$の加重平均
は

$$
\color{red}{\sum_{i=1}^n w_ix_i}
$$

第４章　変数変換

２つの独立な確率変数$X,Y$の線形結合$aX+bY$の分布を考えるとき,変数変換を用いる。

まず,$Z=aX+bY,W=Y$として,$(Z,W)$の分布を考える。

$Z$の確率密度関数は,以下のようにあらわせる。

$$
f_Z(z)=\color{red}{\int_{-\infty}^{\infty} \frac1{|a|}f_X(\frac{z}{a}-\frac{bw}{a})f_Y(w)dw}
$$

第５章　離散型分布

共分散公式：$Cov(X,Y)=\color{red}{E(X,Y)-E(X)E(Y)}$

離散型分布に関しては,ProbabilityDistoributionを参照せよ。

第６章　連続型分布と標本分布

偏差値の公式：

I.２変量正規分布,多変量正規分布

実数$\mu_1,\mu_2$と$\sigma_1>0,\sigma_2>0$,そして$\rho(-1<\rho<1)$に対し,確率ベクトル$X=(X_1,X_2)^\top$が同時確率変数

$$
f(x_1,x_2)=\color{red}{\frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\
\times \exp\biggl[-\frac{1}{2(1-\rho^2)}\biggl(\Big(\frac{x_1-\mu_1}{\sigma_1}\Big)^2-2\rho\Big(\frac{x_1-\mu_1}{\sigma_1}\Big)\Big(\frac{x_2-\mu_2}{\sigma_2}\Big)+\Big(\frac{x_2-\mu_2}{\sigma_2}\Big)^2\biggl)\biggl]}
$$

を持つとき,$X$は平均ベクトル$\mu$,分散共分散行列$\sum$の２変量正規分布に従い,$N_2(\mu,\sum)$で表す。

なお,

$$
E[X]=\mu,V[X]=\sum
$$

であり,$\mu=(0,0)^\top,\sum=I_2$となる場合は,２変量標準正規分布という。

　　

〇多変量正規分布の場合

$p$次元ベクトル$\mu=(\mu_1,...,\mu_p)^\top$と$p \times p$の正定値行列$\sum$に対し,確率ベクトル$X=(X_1,...,X_p)^\top$が同時確率密度関数

$$
f(x)=\color{red}{\frac{1}{(2\pi)^{\frac{p}{2}}(\det\sum)^\frac{1}{2}}\exp\Big(-\frac{1}{2}(x-\mu)^\top{\sum}^{-1}(x-\mu)\Big)}
$$

をもつとき,$X$は平均ベクトル$\mu$,分散共分散行列$\sum$の多変量正規分布に従い,$N_p(\mu,\sum)$で表す。

　　

〇２変量正規分布の条件付分布

２変量$X_1...N(\mu_1,\sigma_1^2)$と$X_2...N(\mu_2,\sigma_2^2)$

$X_1=x_1$が与えられた時の$X_2$の条件付分布は正規分布であり,その期待値と分散は,$\rho$を２変量の相関係数とすると,

$$
E[X_2|X_1=x_1]=\color{red}{\mu_2+\rho\frac{\sigma_2}{\sigma_1}(x_1-\mu_1)}\color{black}=\color{red}{\mu_2+\frac{\sigma_{12}}{\sigma_1^2}(x_1-\mu_1)}
$$

$$
V[X_2|X_1=x_1]=\color{red}{\sigma_2^2(1-\rho^2)}
$$

となる。

第７章　極限定理,漸近理論

I.極値分布

極値分布：

ある累積分布関数にしたがって生じた大きさ$n$の標本$X1,X2, …, Xn$のうち$x$以上 (あるいは以下) となるものの個数がどのように分布するかを表す,連続確率分布モデルのこと。特に最大値や最小値などが漸近的に従う分布。（参考：Wikipedia）

ガンベル分布：

$$F_I(x)=\color{red}{e^{-e^{-y}}}$$

フレシェ分布：

ワイブル分布：

がある。なお,$y$はパラメーターである。上記の公式は最大値に関する分布であり,最小値が漸近的に従う分布は極小値分布と呼ばれ,極大値分布における確率変数$X$を$-X$で置き換えることで得られる。

独立同一分布であれば,最大値及び最小値の分布は,適切に位置・尺度変換することによって,すべて３つの分布のどれかに収束させることができる。

II.デルタ法

平均$\mu$,分散$\sigma^2$の独立同一分布について,$X_1,...,X_n$の標本平均を$\bar{X_n}$とする。

関数$f(\bar{X_n})$について,$\color{red}{\sqrt{n}(f(\bar{X_n})-f(\mu))}$の分布収束先は,$\color{red}{N(0,f^{\prime}(\mu)^2\sigma^2)}$である。

第８章　統計的推定の基礎

I.最尤法・モーメント法・推定値の性質

〇最尤法

確率分布$F_\theta$の確率密度関数を$f(x;\theta)$とし,その同時確率密度関数を$L(\theta):={\displaystyle\prod^n_{i=1}}f(x_i;\theta)$として,これを$\theta$の関数として考えるとき尤度関数と呼び,その値を尤度という。

尤度：得られた標本が確率分布$F_\theta$によってどれだけ生成されやすいかの指標。

最尤推定値：パラメータ領域内において尤度を最大にするパラメータ値。

対数尤度：最尤推定がしやすく加工するため,$\log L(\theta)={\displaystyle\sum^n_{i=1}}\log f(x_i;\theta)$とすることもある。

〇モーメント法

ある確率分布のパラメータを標本から推定しようとするとき,結果となるその確率分布の母数から逆算して計算を行うことであり,母数は$\mu_1,\mu_2...$などで表される。

（例）：ガンマ分布$Ga(\alpha,1/\lambda)$に対して,平均と分散（母数）を$\mu_1=\alpha/\lambda,\mu_2=\alpha/\lambda^2$と置き,逆算するなど。

　　

〇推定量の性質

真のパラメータ値を$\theta$,推定値を$\hat\theta$（標本に依存）とすると,平均二乗誤差（Mean Squared Error）は,

$$
MSE_\theta(\hat\theta):=E_\theta[(\hat\theta-\theta)^2]
$$

であり,推定値がパラメータ値からどれほど離れているかを評価する。

二つの推定値の推定精度を比較する時は,$\hat\theta_1,\hat\theta_2$に対して,

$$
e(\hat\theta_1,\hat\theta_2):=\color{red}{\frac{E_\theta[(\hat\theta_2-\theta)^2]}{E_\theta[(\hat\theta_1-\theta)^2]}}
$$

として計算すればよい。

　　

〇バイアス・バリアンス分解

不偏推定値：$E_\theta[\hat\theta]=\theta$となるような$\hat\theta$

バイアス：$b_\theta(\hat\theta):=E_\theta[\hat\theta]-\theta$

分散の公式：$E[X^2]=E[X]^2+V[X]$

以上より,バイアス・バリアンス分解は,以下で表せる。

$$
E_\theta[(\hat\theta-\theta)^2]=(E_\theta[\hat\theta]-\theta)^2+V_\theta(\hat\theta)=\color{red}{(b_\theta(\hat\theta))^2+V_\theta(\hat\theta)}
$$

意味：バイアス項が０になる不偏推定量に制限したうえで平均二乗誤差を最小にするためには,分散$V[\hat\theta]$を最小にすることと同値である。

また,このような推定量を一様最小分散不偏推定量という。

　　

〇ガウス・マルコフの定理

最小二乗法で求めた最小二乗推定量は,線形不偏推定量の中では分散が最小となる（最良線形不偏推定量）であることを保障した定理。

最小二乗推定量を$\hat\beta$とし,他の線形不偏推定量を$\tilde\beta$とすると,

$$V[\tilde\beta]\geq V[\hat\beta]$$

となる。

II.フィッシャー情報量＆クラーメル・ラオの不等式

フィッシャー情報量は,$f$を確率密度関数あるいは確率変数として,

$$J_n(\theta)=\color{red}{E_\theta[(\frac{\partial}{\partial \theta} \log f(X_1,...,X_n;\theta))^2]}$$

もしくは適当な正則条件のもと同値となる

$$J_n(\theta)=\color{red}{-E_\theta[\frac{\partial^2}{\partial \theta^2} \log f(X_1,...,X_n;\theta)]}$$

により定義される。フィッシャー情報量が正の時,不偏推定量に対するクラーメル・ラオの不等式は

$$\color{red}{V_\theta[\hat{\theta}] \geq J_n(\theta)^{-1}}$$

クラーメル・ラオの不等式を満たすような不偏推定量を有効推定量という。

III.漸近的な性質（中心極限定理,漸近正規性）

〇中心極限定理

標本$X_1,...,X_n$の標本平均を$\bar X_n$とし,母平均$\mu$,母分散$\sigma$とすると,

$$
\color{red}{\sqrt n(\bar X_n-\mu)\mbox{は正規分布}N(0,\sigma^2)\mbox{に分布収束する}}
$$

〇最尤推定量の漸近正規性

最尤推定量$\hat\theta$から極限値の$\theta$を引いたうえで$\sqrt n$でスケーリングした,

$$
\color{red}{Z:=\sqrt n(\hat\theta-\theta)\mbox{は正規分布}N(0,J_1(\theta)^{-1})\mbox{に分布収束する}}
$$

IV.ジャックナイフ法＆リサンプリング法

ジャックナイフ法：

推定量が不偏ではなく,バイアスがある場合,得られている標本を再利用して推定量のバイアスを補正する方法

標本：$X_1,X_2,...,X_n$と推定量$\hat\theta$を考える。

１．標本$X_i$を除いたサイズ$n-1$の部分標本から推定量$\hat\theta$と同様にして求めた推定量を$\hat\theta_{(i)}$とする。

２．１を繰り返して得られた$n$個の推定量の平均を

$$\hat\theta_{(\cdot)}:=\frac{1}{n}\sum^n_{i=1}\hat\theta_{(i)}$$

と書くことにする。

３．この時の$\hat\theta$のバイアスは,（証明は省略するが）$\color{red}{\widehat{bias}:=(n-1)(\hat\theta_{(\cdot)}-\hat\theta)}$で見積もられ,

それを補正することで,ジャックナイフ推定量

$$
\begin{split}
\hat\theta_{jack}:&=\hat\theta-\widehat{bias} \
&=\color{red}{\hat\theta-(n-1)(\hat\theta_{(\cdot)}-\hat\theta)} \
&=\color{red}{n\hat\theta-(n-1)\hat\theta_{(\cdot)}}
\end{split}
$$

が求められる。

リサンプリング法：

ジャックナイフ法のように,得られている標本から部分標本を用いることにより推定精度を高める手法。

第９章　区間推定

I.分散の区間推定

標本平均$\bar{X}$からの偏差平方和を$T^2={\displaystyle\sum^n_{i=1}}(X_i-\bar{X})^2$とする。

$\chi^2={\displaystyle\frac{T^2}{\sigma^2}}$は自由度$n-1$のカイ二乗分布に従い,カイ二乗分布の上側2.5%と下側2.5%点を考えると,

以下の確率式が成り立つ。

$$
P\Biggl(\color{red}{\frac{T^2}{\chi_{0.025}^2(n-1)}\leq\sigma^2\leq\frac{T^2}{\chi_{0.975}^2(n-1)}}\color{black}{\Biggl)=0.95}
$$

II.分散の比の区間推定

２つの独立した集団の分散を比較する。

$X_{11},X_{12},...,X_{1n_1}$が互いに独立に正規分布$N(\mu_1,\sigma_1^2)$に従い,

それとは独立に$X_{21},X_{22},...,X_{2n_2}$が互いに独立に正規分布$N(\mu_2,\sigma_2^2)$に従うとき,

統計量$F={\displaystyle\frac{V_1/\sigma_1^2}{V_2/\sigma_2^2}}$は自由度$(n_1-1,n_2-1)$のF分布に従う。

ちなみに,

である。

自由度$(\phi_1,\phi_2)=(n_1-1,n_2-1)$とすると,分散の比較における９５％信頼区間は以下のようにあらわせる。

$$
P(-1.96 \leq u_i \leq 1.96)=0.95 \quad \mbox{より,}
$$

$$
\color{red}{P \Big(\frac{V_1}{V_2} \cdot \frac{1}{F_{0.025}(\phi_1,\phi_2)} \leq \frac{\sigma_1^2}{\sigma_2^2} \leq \frac{V_1}{V_2} \frac{1}{F_{0.975}(\phi_1,\phi_2)}\Big)=0.95}
$$

III.多項分布の信頼区間

確率$p_i$で事象$A_i(i=1,2...,k)$が起こる試行を$n$回行い,それぞれの事象が起こる回数$N_i$は多項分布に従い,

多項分布の平均：$E[N_i]=np_i$

多項分布の分散：$V[N_i]=np_i(1-p_i)$である。

ここで,$\hat p_i=\frac{N_i}{n}$（事象$A_i$の回数/試行回数：$p_i$の実現値）とし,

$$u_i=\color{red}{\frac{\hat p_i-p_i}{\sqrt{\hat{p_i}(1-\hat{p_i})/n}}}$$

とすると,$u_i$は漸近的に標準正規分布に従うため,$P(-1.96 \leq u_i \leq 1.96)=0.95$が成り立つため,多項分布における$p_i$の９５％信頼区間は,

$$
\color{red}{P \Big(\hat p_i-1.96\sqrt{\frac{\hat{p_i}(1-\hat{p_i})}{n}} \leq p_i \leq \hat p_i+1.96\sqrt{\frac{\hat{p_i}(1-\hat{p_i})}{n}}\Big)}
$$

IV.多項分布の差の信頼区間

多項分布に従う確率変数$N_i(i=1,2,...,k)$における$N_1,N_2$の共分散は,

$$
\begin{split}
Cov[N_1,N_2] &= E[N_1,N_2]-E[N_1]E[N_2] \
&=n(n-1)p_1p_2-n^2p_1p_2 \
&=\color{red}{-np_1p_2}
\end{split}
$$

として負の値であらわされ,事象$A_1$が起こる回数が増えれば,事象$A_2$が起こる確率が減ることを意味する。

多項分布の差$p_1-p_2$を求めるために,$\hat p_1-\hat p_2=\frac{N_1}{n}-\frac{N_2}{n}$における,

期待値：$E[\hat p_1-\hat p_2]=\color{red}{p_1-p_2}$

分散：$V[\hat p_1-\hat p_2]=\color{red}{{\displaystyle\frac{p_1(1-p_1)}{n}+\frac{p_2(1-p_2)}{n}+\frac{2p_1p_2}{n}}}$

（分散は,二項分布の分散公式と上の共分散公式を利用）

$$
u = \color{red}{\frac{(\hat p_1-\hat p_2)-(p_1-p_2)}{\sqrt{\frac{\hat p_1(1-\hat p_1)}{n}+\frac{\hat p_2(1-\hat p_2)}{n}+\frac{2 \hat p_1 \hat p_2}{n}}}}
$$

とすると,uは漸近的に標準正規分布に従うので,

$p_1-p_2$の９５％信頼区間は,

$$
P(-1.96 \leq u_i \leq 1.96)=0.95 \quad \mbox{より,}
$$

$$
\color{red}{(\hat p_1-\hat p_2)-1.96\sqrt{\frac{\hat p_1(1-\hat p_1)}{n}+\frac{\hat p_2(1-\hat p_2)}{n}+\frac{2 \hat p_1 \hat p_2}{n}}}
$$

$$
\color{red}{(\hat p_1-\hat p_2)+1.96\sqrt{\frac{\hat p_1(1-\hat p_1)}{n}+\frac{\hat p_2(1-\hat p_2)}{n}+\frac{2 \hat p_1 \hat p_2}{n}}}
$$

第１１章　正規分布に関する検定

１標本の平均の検定（分散が既知）

検定統計量$Z$：$Z=\color{red}{{\displaystyle\frac{\bar{x}-\mu_0}{\frac{\sigma}{\sqrt{n}}}}}$

１標本の平均の検定（分散が未知）

検定統計量$T$：$T=\color{red}{{\displaystyle\frac{\bar{X}-\mu_0}{s/\sqrt{n}}}}$

ただし,$s$は不偏分散$s^2=\color{red}{\frac1{n-1}{\displaystyle\sum_{i=1}^n}(X_i-\bar{X})^2}$で,

自由度$n-1$の$t$分布に従う。

２標本の平均の検定（分散が既知）

群AとBがあり,

群$A$の参加者の確率変数を$X_{Ai}$とし,互いに独立に平均$\mu_A$,分散${\sigma_A}^2$の正規分布に従うとする。

分散${\sigma_A}^2$と${\sigma_B}^2$は既知とする（実際には想定しにくい）。

また,群Aと群Bの差を$\delta=\mu_A-\mu_B$とし,帰無仮説を$H_0:\delta=\delta_0$とする。

検定統計量$Z$：

$$
Z=\color{red}{\frac{\bar{X_A}-\bar{X_B}-\delta_0}{\sqrt{\frac{{\sigma_A}^2}{n_A}+\frac{{\sigma_B}^2}{n_B}}}}
$$

ただし,$\delta_0=0$（２間の平均が等しい）として設定することが多い。

２標本の平均の検定（分散が未知）

各群について,分散の不偏推定量を,

${s_A}^2=\color{red}{\frac1{n_A-1}{\displaystyle\sum_{i=1}^{n_A}}(X_{Ai}-\bar{X_A})^2}$のようにすると,

共通の母分散${\sigma_A}^2={\sigma_B}^2=\sigma^2$を仮定すると,２つの群をプールした標本不偏分散

$$
s^2=\color{red}{\frac{(n_A-1){s_A}^2+(n_B-1){s_B}^2}{n_A+n_B-2}}
$$

が得られる。

帰無仮説$H_0:\delta=\delta_0$のもとで,検定統計量$T$は,

$$
T=\color{red}{\frac{\bar{X_A}-\bar{X_B}-\delta_0}{s\sqrt{\frac1{n_A}+\frac1{n_B}}}}
$$

で,自由度$n_A+n_B-2$の$t$分布に従う。

１標本の分散の検定

平均$\mu$は未知とする。分散に関する帰無仮説を$H_0:\sigma^2=\sigma_0^2$としたとき,

検定統計量$V$

$$
V=\color{red}{\frac{(n-1)s^2}{\sigma_0^2}}
$$

は自由度$n-1$のカイ二乗分布に従う。

２標本の分散の検定

二つの群の平均$\mu_A,\mu_B$は未知とする。

二群の分散における帰無仮説を$H_0:\sigma_A^2=\sigma_B^2$としたとき,

検定統計量$F$

は,自由度$(n_B-1,n_A-1)$の$F$分布に従う。

第１２章　一般の分布に関する検定法

母比率の検定

帰無仮説：事象発生の確率は$\theta_0$である。

施行によって計算された確率を$\hat{\theta}$とし,試行回数を$n$とすると,

検定統計量は,

$$
z=\color{red}{\frac{\hat{\theta}-\theta_0}{\sqrt{\frac{\theta_0(1-\theta_0)}{n}}}}
$$

となる。

母比率の差の検定

試行回数$n_1$,成功確率$\theta_1$（二項分布）の確率変数$X_1$と,

試行回数$n_2$,成功確率$\theta_2$（二項分布）の確率変数$X_2$について,

母比率の差の有意性を調べたいとき,

帰無仮説：$\theta_1=\theta_2$（両辺の確率はわからなくてもいい。）とし,最尤推定量を$\hat\theta_i$とすると,

検定統計量は,

$$
z=\frac{\color{red}{\hat\theta_1-\hat\theta_2}}{\hat\theta\color{red}{(1-}\color{black}{\hat\theta}\color{red}{)\Big(\frac{1}{n_1}+\frac{1}{n_2}\Big)}} \quad, \quad \hat\theta=\color{red}{\frac{n_1\hat\theta_1+n_2\hat\theta_2}{n_1+n_2}}
$$

となる。

適合度検定

カテゴリの個数を$I$,それぞれの生起確率を$p_i$,総観測度数を$n$,期待度数(生起確率×総観測度数n)を$np_i$とすると,

カイ二乗適合度検定の検定統計量は

$$
T(x)=\color{red}{\sum^I_{i=1}\frac{(x_i-np_i)^2}{np_i}}, x=(x_1...,x_I)
$$

となる。

自由度は$d=\color{red}{I-1-k}$であり,$k$は例えばポアソン分布の条件などでパラメータを用いるごとに増えていく。

尤度比検定

尤度比検定は,「帰無仮説が正しいとしたときの最大尤度（帰無仮説の最大尤度とする）」と「尤度関数全体を考慮した最大尤度（全体の最大尤度とする）」を比較する検定法である。

サイズ$n$の標本$X$が,$X_1=x_1,X_2=x_2,...,X_n=x_n$を満たすとし,$\theta$をパラメータとする。確率関数を$f(x;\theta)$（：母集団から取り出した標本が$x$である）と定義すると,尤度関数は,

$$
L(\theta)=f(x_1;\theta)\cdot f(x_2;\theta)\cdot ...\cdot f(x_n;\theta)
$$
となる。

　　

母数空間を$\Theta$,その次元数を$\beta$,母数空間における（帰無仮説が正しい時の）部分空間を$\Theta_0$,その次元数を$\alpha$とし,$\Theta$での最尤推定値を$\hat\theta$,$\Theta_0$での最尤推定値を$\hat\theta_0$とする。この時,帰無仮説は,

母数$\theta$は母数空間$\Theta$の特定の部分集合$\Theta_0$に含まれる(wikipedia)

つまり,帰無仮説：$\Theta$で考えた$\hat\theta=\Theta_0$で考えた$\hat\theta_0$

この尤度関数について,$\theta$の最尤推定値を求めて,最大尤度が求まるとき,尤度比は,

$$
\lambda_n=\color{red}{\frac{\mbox{帰無仮説の最大尤度}}{\mbox{全体の最大尤度}}}\color{black}{=\frac{L(X,\hat\theta_0)}{L(X,\hat\theta)}}
$$

となる。また,$n$を無限大にして,$2\log\lambda_n$を計算すると,対数にすることで差として表せることから,

$2\log\lambda_n$は自由度$\color{red}{\beta-\alpha}$のカイ二乗分布に従うことが示せる。

第１３章　ノンパラメトリック法

検定内容	検定名
２群の差の検定	ウィルコクソンの順位和検定,並べ替え検定
対応がある場合の差の検定	（ウィルコクソンの）符号付き順位検定,符号検定
３群以上の差の検定	クラスカル・ウォリス検定

　　

I.2群の差の検定

ウィルコクソンの順位和検定

　　

２つの群A,Bに関して,

帰無仮説：二つの群の分布が同じ

対立仮説：片方の群がずれている（高い＆低いなど）

P値は,対象となる群(A群とする)に関して,

$$
\mbox{P値}=\color{red}{\frac{\mbox{A群の順位和が今の順位和以下となる組み合わせ}}{\mbox{A群の順位の組み合わせ}}}
$$

各群のサンプルサイズ$m$と$n$が大きく,タイがない場合,

平均$=\color{red}{{\displaystyle\frac{m(m+n+1)}{2}}}$

分散$=\color{red}{{\displaystyle\frac{mn(m+n+1)}{12}}}$

II.対応がある場合の差の検定

符号付き順位検定

　　

帰無仮説：分布の中央値が0

対立仮説：分布の中央値が0より大きい

サンプルサイズを$n$とする（値が0のものは観測値として除く）。符号付き順位において,

符号と順位の組み合わせ：$2^n$

正値の合計が,「標本における正値の合計」以上となる組み合わせ：標本正値以上組み合わせ（とする）

を用いることで,Ｐ値を

$$
\mbox{P値}=\color{red}{\frac{\mbox{標本正値以上組み合わせ}}{2^n}}
$$

で表すことができる。

サンプルサイズ$n$が大きいとき,

平均：$\color{red}{n(n+1)/4}$

分散：$\color{red}{n(n+1)(2n+1)/24}$

符号検定(符号付き順位検定との違い)

　　

帰無仮説と対立仮説は同じ。

検定統計量では,「正値の個数」を用い,二項分布$Bin(n,0.5)$に従わせる。

つまり,片側P値は,6つの標本のうち4つが正値だとすると,

$$
P(T_+\geq4)=(_6C_4+_6C_5+_6C_6)\times(0.5)^6
$$

となる。

III.3群以上の差の検定

クラスカル・ウォリス検定（２群以上で可）

　　

３群の場合について考える。

群A,B,Cについて,サンプルサイズ$N$を$N=n_A+n_B+n_C$として考える。

順位の中央値を$\tilde N=(N+1)/2$とし,各群の順位和と順位の平均を$R_A,R_B,R_C$と$\bar R_A,\bar R_B,\bar R_C$とする時,タイが無い場合のクラスカル・ウォリス検定の検定統計量は,

$$
H=\color{red}{\frac{12}{N(N+1)}\big(n_A(\bar R_A-\tilde N)^2+n_B(\bar R_B-\tilde N)^2+n_C(\bar R_C-\tilde N)^2\big)}
$$

または,

$$
H=\color{red}{\frac{12}{N(N+1)}\bigg(\frac{{R_A}^2}{n_A}+\frac{{R_B}^2}{n_B}+\frac{{R_C}^2}{n_C}\bigg)-3(N+1)}
$$

となる。

各群のサンプルサイズが大きいときには,自由度(群の数-1)のカイ二乗分布に従う。

IV.順位相関係数

順位相関係数：２次元データがともに順位データである時の相関係数。

〇スピアマンの順位相関係数

$$
r_s=\color{red}{1-\frac{6{\displaystyle\sum^n_{i=1}}(x_i-y_i)^2}{n(n^2-1)}}
$$

〇ケンドールの順位相関係数

$(x_i,y_i),(x_j,y_j)\quad(i \neq j)$に対して,$(x_i-x_j)(y_i-y_j)$が正となる組の数を$P$,負となる組の数を$N$とする。

この時,ケンドールの順位相関係数は,

$$
r_k=\color{red}{\frac{P-N}{n(n-1)/2}}
$$

第１４章　マルコフ連鎖

マルコフ連鎖：現在の状態$X_n$が与えられれば,それ以外の過去の情報は未来$X_{n+1}$を予測するのに不要であるという性質

斉時的：$X$における$m$ステップの推移確率が時点$n$によらないとき,マルコフ連鎖$X$は斉時的である。

有限マルコフ連鎖：状態空間（時点$n$における状態$X_n$がとる値の空間）が離散的である場合。

I.推移確率

〇推移確率行列:

$S=1,2,...,N$であり,状態$i$から状態$j$への$m$ステップでの推移確率を$p_m(i,j)$とすると,以下のようになる。

$m=1$の時は,

$$p(i,j):=p_1(i,j),\quad Q:=Q(1)$$

と表す。

〇推移確率の性質

$X_n$に対して$p_n(k):=P(X_n=k)$とすると,

$$
\pi_n=(p_n(1),p_n(2),...,p_n(N))
$$

となるN次元行ベクトルは,状態空間$X_n$におけるそれぞれの確率のベクトルとして表せるため,状態確率ベクトルといい,$\pi_0$を初期分布という。ここで,以下が言える

(1)任意の自然数$l,m$に対して,

$$
Q(m+l)=\color{red}{Q(m)Q(l)=Q^mQ^l}
$$

(2)任意の$n=0,1,2...$に対して,

$$
\pi_n=\color{red}{\pi_0Q^n}
$$

〇定常分布

状態確率ベクトル$\pi_n$において$n \rightarrow \infty$としたとき,

$$\pi := \lim_{n\to\infty}\pi_n \mbox{について,}$$

$$\pi=\color{red}{\pi Q}$$

が成り立ち,$X$の定常分布という。

初期分布が定常分布であるマルコフ連鎖を定常マルコフ連鎖という。

第１５章　確率過程の基礎

確率過程：時点$\mapsto$観測値となる観測値を用いた関数を表すことができ,これをパスという。

I.独立定常増分とブラウン運動

〇独立定常増分

　　

(1)独立増分性

任意の$0=t_0<t_1<...<t_{n-1}<t_n$に対して,$X_{t_0},X_{t_1}-X_{t_0},X_{t_2}-X_{t_1},...,X_{t_n}-X_{t_{n-1}}$は互いに独立である。

(2)定常増分性

任意の$0 \leq t <t+h$に対して,$X_{t+h}-X_t$の分布は,$X_h-X_0$の分布と同一である。

　　

〇ブラウン運動

$B_0=0$なる確率過程$B=(B_t)_{t \geq0}$が以下の性質を満たす。

　　

(1)$B$は独立定常増分である。

(2)各$t\geq 0$に対して,（周辺分布）$B_t \sim N(\mu t,\sigma^2t)$

(3)$B$のパスは連続である。

　　

(2)において,$\mu=0,\sigma^2=1$となる場合,標準ブラウン運動またはウィナー過程という。

II.ブラウン運動のパラメータ推定

観測データは離散的に集めることの方が多いため,$B_t \sim N(\mu t,\sigma^2t)$なるブラウン運動のパスを時間間隔$\Delta>0$で観測し,$B_0,B_\Delta,B_{2\Delta},...,B_{n\Delta}$を得たと仮定してパラメータ$\mu,\sigma^2$を推定する。

　　

まず,$Z_k :=B_{k\Delta}-B_{(k-1)\Delta}\sim N(\hat\mu\Delta,\hat\sigma^2\Delta), \quad (k=1,...,n)$らは独立である。

$\hat\mu\Delta,\hat\sigma^2\Delta$は以下のように書くことができ,

$$
\begin{split}
\hat\mu\Delta&=\color{red}{\frac{1}{n}\sum^n_{k=1}Z_k},\
\hat\sigma^2\Delta&=\color{red}{\frac{1}{n}\sum^n_{k=1}{Z_k}^2-\Biggl(\frac{1}{n}\sum^n_{i=1}Z_k \Biggl)^2}
\end{split}
$$

この最尤推定量は$\Delta$を固定して$n$が無限大になるときに真値に収束することが知られている。

III.ポアソン過程

各$t$で自然数値をとる確率過程$N=(N_t)_{t\geq0}$を考え,$N_0=0$とする。この$N$が以下の(1),(2)の性質を満たすとき,強度$\lambda$のポアソン過程という。

(1)$N$は独立定常増分過程である。

(2)任意の$t\geq0$に対して$N_t$は強度$\lambda t$のポアソン分布に従う。すなわち,

$$
P(N_t=k)=\color{red}{e^{-\lambda t}\frac{(\lambda t)^k}{k!}}, \quad k=0,1,2,...
$$

ポアソン過程は連続時間確率過程だが,自然数にしか値をとらない階段型のパスであるため,何らかのイベントの回数を表すモデルとして用いられることが多い。

　　

ポアソン過程のパラメータ推定

　　

強度$\lambda$をもつポアソン過程のパラメータ$\lambda$推定するとき,以下のデータ形式を考える。

(I)イベントの起こった時刻$T_1,T_2,...,T_n$を観測する。

・イベント発生の正確な時刻がわかる。

・$n$はイベント発生の回数である。

　　

(II)時間間隔$\Delta>0$によってデータ$N_0,N_\Delta,N_{2\Delta},...,N_{n\Delta}$を観測する。

・イベントの正確な時刻は観測されず,その回数しかわからない。

・$n$は観測の回数である。

〇**(I)の場合の推定**

$W_k=T_k-T_{k-1}$として,データを$W_1,W_2,...,W_n$（次にイベントが起こるまでの時間）に変換すると,平均$1/\lambda$の指数分布に従うため,対数尤度関数をとると,

$$
l_n(\lambda)=\sum^n_{i=1}\log f_{\lambda}(W_k)=n \log\lambda-\lambda\sum^n_{i=1}W_k
$$

よって最尤推定量は,

$$
\hat\lambda=\Biggl(\frac{1}{n}\sum^n_{i=1}W_k \Biggl)^{-1}=\color{red}{\frac{n}{T_n}}
$$

　　

〇**(II)の場合の推定**

$M_k=N_{k\Delta}-N_{(k-1)\Delta}$としてデータを$M_1,...,M_n$に変換すると,ポアソン過程の独立定常増分性により,独立に$M_k \sim Po(\lambda\Delta)$となるので,

同様に対数尤度関数から最尤推定量を求めると,

$$
\hat\lambda=\frac{1}{n\Delta}\sum^n_{k=1}M_k=\color{red}{\frac{N_{n\Delta}}{n\Delta}}
$$

となる。

*(1),(2)のいずれにおいても,

$$
\hat\lambda=\color{red}{\frac{(\mbox{イベントの総回数})}{(\mbox{観測時間})}}
$$

と書くことができる。

　　

複合ポアソン過程

　　

ポアソン過程の応用として以下のような確率過程がある。

$$
X_t=\sum^{N_t}_{k=1}U_k
$$

ただし,$N=(N_t){t\geq0}$はポアソン過程で,$(U_k){k=1,2,...}$は互いに独立に同一の分布に従う確率変数列で,$N$とも独立とする。このような確率過程$X=(X_t)_{t\geq0}$は複合ポアソン過程という。

とくに$U_k\equiv 1$の場合は$X$はポアソン過程である。

〇複合ポアソン過程は,第$k$回目のイバント発生に対応する何らかの量$U_k$の累積和を表すモデルである。

例えば,時刻$t$までの地震の発生回数を$N_t$というポアソン過程で表すとき,$k$回目の地震時の損害額を$U_k$とすると,$X_t$は時刻$t$までの地震による総損害額をあらわせる。

　　

〇複合ポアソン過程の推定

$X$を複合ポアソン過程であるとする。

例えば,ポアソン過程に対してその累積値が正規分布に従うとき（$E[N_t]=\lambda t,E[U_k]=\mu,V[U_k]=\sigma^2$）,$N_t,U_k$の独立性から,

$$
E[X_t]=E\Bigg[\sum^{N_t}_{k=1}E[U_k] \Bigg]=\color{red}{\mu E[N_t]=\lambda\mu t}
$$

$$
V[X_t]=E[{X_t}^2]-(E[X_t])^2=\color{red}{\lambda t(\mu^2+\sigma^2)}
$$

例えば,ポアソン過程に対してその累積値がベルヌーイ分布に従うとき（$E[N_t]=\lambda ,E[U_k]=q,V[U_k]=q(1-q)$）,$N_t,U_k$の独立性から,

$$
E[X_t]=\lambda q, \quad V[X_t]=\lambda(q^2+q(1-q))=\lambda q
$$

要するに、

$$
\begin{split}
E[x_t]&=\color{red}{E[N_t]\times E[U_k]}\
V[X_t]&=\color{red}{E[N_t]\times\Bigg(\Big(E[U_k]\Big)^2 +V[U_k] \Bigg)}
\end{split}
$$

である。

第１６章　重回帰分析

I.単純回帰モデル

説明変数$x$と被説明変数$y$について,回帰式を,

$$y_i=\beta_0+\beta_1x_i+u_i, \quad i=1,2...,n$$

とし,最小自乗推定量を$\hat\beta_0,\hat\beta_1$とすると,

$$
\hat\beta_1=\color{red}{\frac{{\displaystyle\sum^n_{i=1}}(x_i-\bar{x})(y_i-\bar{y})}{{\displaystyle\sum^n_{i=1}}(x_i-\bar{x})^2}}
$$

$$
\hat\beta_0=\color{red}{\bar{y}-\hat\beta_1\bar{x}}
$$

が得られる。

II.推定量の性質

回帰係数の推定量を$\hat\beta$とすると,

〇不偏性：最小二乗推定量は不偏性をもつ。$E(\hat\beta)=\beta$

〇最小分散（ガウス・マルコフの定理）：最小二乗推定量の分散は最も小さい。

〇誤差項の分散の推定量：説明変数の個数を$p$として,

$$
s^2=\color{red}{\frac{{\displaystyle\sum^n_{i=1}}e^2_i}{n-p-1}}
$$
となる。

III.決定係数

決定係数：モデルで説明できる部分の割合（$\mbox{回帰式の変動}/\mbox{全変動}$）

$$
R^2 = \color{red}{\frac{{\displaystyle\sum^n_{i=1}}(\hat{y_i}-\bar{y})^2}{{\displaystyle\sum^n_{i=1}}(y_i-\bar{y})^2}}\color{black}{=}\color{red}{1-\frac{{\displaystyle\sum^n_{i=1}}e^2_i}{{\displaystyle\sum^n_{i=1}}(y_i-\bar{y})^2}}
$$

自由度調整済み決定係数

$n$個の標本と$p$個の説明変数があるとき,自由度調整済み決定係数は,

$$
\bar{R^2}=\color{red}{1-\frac{{\displaystyle\sum^n_{i=1}}e^2_i/(n-p-1)}{{\displaystyle\sum^n_{i=1}}(y_i-\bar{y})^2/(n-1)}}
$$

で表せる。

IV.重回帰分析の検定

〇誤差項の分散のt検定（各偏回帰係数の検定）

$n \quad(i=1...n)$個の標本と$p$個の説明変数について,

帰無仮説：$H_0:\beta_i=\beta^0_i$

対立仮説：$H_1:\beta_i \neq \beta^0_i$

また,標準誤差を$SE(\hat\beta_i)$とすると,検定統計量tは,

$$
t=\color{red}{\frac{\hat\beta_i-\beta^0_i}{SE(\hat\beta_i)}}\color{black}\sim t(n-p-1)
$$

となる。

〇線形制約の検定

次の回帰モデル＊を考える。

$$
y_i=\beta_0+\beta_1x_{i1}+...+\beta_px_{ip}+u_i, \quad i=1,2,...,n
$$

$$
E(u_i)=0, \quad E(u_i^2)=\sigma^2, \quad E(u_iu_j)=0 \quad (i \neq j)
$$

偏回帰係数が集合したベクトルを$\beta$とする。

《検定の例》

パターン１

帰無仮説$H_0:A\beta=0$

対立仮説$H_1:A\beta \neq 0$

パターン２

帰無仮説$H_0:\beta_i+\beta_j=1$

対立仮説$H_1:\beta_i+\beta_j \neq 1$

例えば,$A=(0,...,0,1,0,...,0)$のように,$k+1$番目の要素が1であるとき,

帰無仮説は$\beta_k=0$となる。

また,無制約モデル（もともとのモデル＊）での残差二乗和：$RSS^u$

制約付きモデル（帰無仮説を考慮したモデル）の残差二乗和：$RSS^r$とする。

そして,以下を定義する。

$$
q=\color{red}{\mbox{(無制約モデルの回帰係数の数)}-\mbox{(制約付きモデルの回帰係数の数)}}
$$

検定統計量$F$は,

$$
F = \color{red}{\frac{(RSS^r-RSS^u)/q}{RSS^u/(n-p-1)}}
$$
として,自由度$(q, n-p-1)$のF分布に従う。

V.正則化

正則化：過学習を防ぐ

説明変数の個数をp,サンプル数をnとし,$\beta$を偏回帰係数,つまり説明変数の重みとする。

また,$\lambda$を正則化パラメータ（任意選択変数）とする。

〇$L_2$正則化によるリッジ回帰

$$
\sum_{i=1}^n(y^{(i)}-\hat y^{(i)})^2+\color{red}{\lambda\sum^p_{j=1}\beta_j^2}
$$

$\lambda$を大きくしていくことで,モデルの重みを相対的に小さくし,過学習を防ぐ。

＊リッジ回帰では,重みが完全には０にならない性質があるため,説明変数が多いと複雑になる。

〇$L_1$正則化によるLasso回帰

$$
\sum_{i=1}^n(y^{(i)}-\hat y^{(i)})^2+\color{red}{\lambda\sum^p_{j=1}|\beta_j|}
$$

＊Lasso回帰ではいくつかの重みは０になることがありうるため,高次元において有効。つまり,自動的に変数選択が行える。

＊ただし,２つの相関の強い変数がある場合はどちらかを選択する必要があり,不安定。

〇Elastic Netによる回帰

$$
\sum_{i=1}^n(y^{(i)}-\hat y^{(i)})^2+\color{red}{\lambda_1\sum^p_{j=1}\beta_j^2-\lambda_2\sum^p_{j=1}|\beta_j|}
$$

《感覚的な理解》

L1正則化項の「０にはならないけどとても小さい重み」を,L2正則化項の「とても小さいけど０になることができない重み」から引くことで実質的に重みを０とし,リッジとLasso回帰のデメリットを打ち消すことができている。

第１７章　回帰診断法

leverage（てこ比,てこ値）とCookの距離

$n \times p$の説明変数行列$X$のランクが$p$であれば,$\hat\beta=(X^{\top}X)^{-1}X^{\top}y$は$\beta$の最小二乗法による推定量となり,

$H=X(X^{\top}X)^{-1}X^{\top}=(h_{ij})$予測値は,$\hat y=Hy$と書くことができる。このとき,

　　

leverage：

$H=(h_{ij})$をハット行列をいい,この時の$i$番目の対角要素$h_{ii}$を$i$番目の観測値のleverageという。

　　

Cookの距離：

標準化された残差と$h_{ij}/(1-h_{ij})$によって計算される。全ての観測値を用いた場合の予測値と,$i$番目の観測値を除いた場合の予測値との差異に関する距離と考えればよく,leverageと同様,各観測地へのモデルへの影響力を示す。

0.5を超えるとその観測値の影響力は大きく,外れ値とされる。

　　

＊自己相関とDW比については,２７章で述べる。

第１８章　質的回帰

I.ロジスティック回帰モデル

ロジスティック回帰モデル：２値応答に対する統計モデル

応答を表す確率変数$Y$が${0,1}$の２値変数であるとき,その期待値を$\pi=E[Y]$とし,$0<\pi<1$を仮定する。この時$Y$は生起確率$\pi$のベルヌーイ分布に従う。

$p$個の説明変数$x_1,...,x_p$を定めたとき,ロジスティック回帰モデルは,

$$
\beta_0+\beta_1 x_1+...+\beta_p x_p = \color{red}{\log \frac{\pi}{1-\pi}}
$$

として表すことができる。

この時,左辺ではオッズ（$P(\bar A)$に対する$P(A)$の比）がもちいられており,対数をとることでとりうる値の範囲を無限大にして２値の判定を可能にする。

オッズに注意したロジスティック回帰モデルは,

$$
\frac{\pi}{1-\pi}=\exp (\beta_0+\beta_1x_1+...+\beta_px_p)=\color{red}{e^{\beta_0}(e^{\beta_1})^{x_1} \cdot \cdot \cdot (e^{\beta_p})^{x_p}}
$$

で表すことができ,$\beta_j$の値は,説明変数$x_j$の値の変化が$Y$のオッズへ与える寄与の大きさを表す。

また,ここから$\pi$自体を求める場合は,左辺を$logit$と置き換えると,逆変換である

$$
\pi=\color{red}{\frac{\exp(logit)}{1+\exp(logit)}}
$$

で求めることができる。

II.プロビットモデル

２値応答に対するもう一つの代表的なモデルは,標準正規分布の累積分布関数

$$
\Phi(x)=\int^x_{-\infty} \frac{1}{\sqrt{2 \pi}}e^{-\frac{1}{2}y^2}dy
$$

を用いて,

$$
\pi = \color{red}{\Phi(\beta_0+\beta_1x_1+...+\beta_px_p)}
$$
とするモデルであり,$\Phi(x)$の逆変換はプロビット変換というから,このモデルは,プロビット関数$\Phi^{-1}:(0,1)\rightarrow(-\infty,\infty)$をリンク関数とする一般化線形モデルであり,プロビットモデルと呼ばれる。

　　

〇潜在変数の仮定

２値の応答変数$Y$の背後には,観測できない潜在変数$Y^$が存在して,この$Y^$は正規分布$N(\mu,\sigma^2)$にしたがって分布すると仮定する。$Y$の値は,

「一定の致死量を超えて毒物を摂取すると死に至る」などといった解釈を例にとると,

として考えられ,この$Y^$の期待値$E[Y^]=\mu$に関して,母数の線形構造

$$
\mu=\beta_0^*+\beta_1^*x_1+...+\beta_p^*x_p
$$

を仮定すれば,$\pi=E[Y]$としてプロビットモデルが得られる。

　　

〇限界効果

プロビットモデルでは,説明変数$x_j$の効果の大きさを

$$
\frac{\partial \pi}{\partial x_j}=\frac{\partial \Phi(\beta_0+\beta_1x_1+...+\beta_px_p)}{\partial x_j}=\color{red}{\varphi(\beta_0+\beta_1x_1+...+\beta_px_p)\beta_j}
$$

で評価する。この時の$\varphi(x)$は標準正規分布の確率密度関数であり,この値を限界効果と呼ぶ。

III.ポアソン回帰モデル（詳細は２８章）

応答が計数値である場合の統計モデル。確率変数$Y$の期待値を$\pi=E[Y]$とし,$\pi>0$を仮定する。また,$Y$は平均$\pi$のポアソン分布に従うと仮定する。この時,ポアソン回帰モデルは,

$$
\log \pi=\beta_0+\beta_1x_1+...+\beta_px_p
$$

で表せる。

２８章で詳しく説明する。

IV.一般化線形モデル

一般化線形モデル：

ロジスティック回帰モデル,プロビットモデル,ポアソン回帰モデルは,一般化線形モデルとして統一的に扱うことができる。

応答を表す確率変数$Y$の期待値を$\pi=E[Y]$とする。$Y$の確率分布として**（一変数）指数型分布**

$$
f(y;\theta,\phi)=\color{red}{\exp\Big[\frac{y\theta-b(\theta)}{a(\phi)}-c(y,\phi) \Big]}
$$

を仮定し,母数$\theta$を正準母数と呼ぶ。

計算により,

$$
\begin{split}
\pi=E[Y]=\color{red}{b'(\theta)} \
V[Y]=\color{red}{b''(\theta)a(\phi)}
\end{split}
$$

が得られるから,正準母数$\theta$は,期待値母数$\pi$のみの関数であることがわかる。

また,関数$a(\phi)$は$a(\phi)=\phi/\omega$の形で表されることが多く,その場合の母数$\phi$散らばり母数と呼ばれる。

一般化線形モデルは,期待値母数$\pi$の滑らかな変換$g(\cdot)$を考え,これが説明変数の線形結合として

$$
g(\pi)=\beta_0+\beta_1x_1+...+\beta_px_p
$$

と表されると仮定する時,関数$g$を**リンク関数（または連結関数）**という。

　　

正規分布：リンク関数を$g(\pi)=\pi$で,通常の線形モデル

　　

ベルヌーイ分布：

〇リンク関数をロジット関数$g(\pi)=\log(\pi/(1-\pi))$としたものが,ロジスティック回帰モデル

〇リンク関数をプロビット関数$g(\pi)=\Phi^{-1}(\pi)$としたものが,プロビットモデルである。

　　

ポアソン分布：リンク関数を対数関数$g(\pi)=\log \pi$としたものが,ポアソン回帰モデル（対数線形モデル）

第１９章　回帰分析その他

I.トービットモデル

被説明変数がある限られた範囲の値しかとらない状況や,一定の条件が満たされるとき,データが観測できないほどの状況がしばしばある。

説明変数に左打ち切りまたは右打ち切りが発生する場合の線形モデルはトービットモデルまたは打ち切り回帰モデルとも呼ばれる。

II.タイプIトービットモデル

$y_i$の実際の観測値$y_i^$を潜在変数とする。潜在変数$y_i^$に打ち切りが伴うが,説明変数$x_i$は常に観測可能である。

タイプIトービットモデルにおいて,観測値$y_i$と潜在変数$y_i^*$の関係は,$L,U$を定数として以下の３つのケースに分けられる。

左打ち切りが伴う場合：

右打ち切りが伴う場合：

両側打ち切りが伴う場合：

III.尤度関数

次のタイプIトービットモデルを考える。

$$
y_i^*=x_i^\top \beta+ \varepsilon_i \quad ,\quad i=1,...,n
$$

$\beta$はパラメータからなるベクトルで,$\varepsilon_i$は互いに独立に正規分布$N(0,\sigma^2)$に従うとする。また,定義関数を以下のよう定める。

次に,$\varphi(\cdot),\Phi(\cdot)$をそれぞれ標準正規分布の確率密度関数,累積分布関数とする。打ち切られる確率$P(y_i^* \leq L)$を考慮すると,$\beta,\sigma$に関する尤度関数は次のようになる。

$$
L(\beta,\sigma)=\color{red}{\prod_{i: \quad y_i>L}\frac{1}{\sigma}\varphi \Big(\frac{y_i-x_i^\top\beta}{\sigma} \Big) \prod_{i: \quad y_i \leq L}\Phi \Big(\frac{L-x_i^\top\beta}{\sigma} \Big)}
$$

IV.生存時間解析

ある時点から,興味のあるイベント（病気の転移,完治,死亡）が観察されるまでの時間$T(\geq 0)$を生存時間という。

考えるべき生存関数は,

$$
S(t)=P(T>t)=\color{red}{\int^{\infty}_t f(x|\theta)dx}
$$

である。$f(x|\theta)$は確率密度関数で,$\theta$は未知のパラメータである。生存関数$S(t)$は,h$t$を超える確率を表している。

V.ハザード関数の例

〇健康状態が安定な人に対するモデルの場合

生存時間$T$が指数分布に従い,確率密度関数を$f(t)=\lambda e^{-\lambda t}$とする。この時の生存関数は$S(t)=\color{red}{e^{-\lambda t}}$で,ハザード関数は$h(t)=\color{red}{\lambda}$となる。定常なハザードであるので,健康状態が安定した人に対するモデルである。

　　

〇病気を持つ人に対するモデルの場合

生存時間$T$がワイブル分布に従い,確率密度関数を$f(t)=\lambda p(\lambda t)^{p-1}e^{-(\lambda t)^p}$とする。なお,ワイブル分布は,指数分布を一般化したモデルである。この時のハザード関数は$h(t)=\color{red}{\lambda p(\lambda t)^{p-1}}$となる。

$p=1$のとき,$h(t)$は定数。

$p>1$のとき,$h(t)$は単調増加。

$p<1$のとき,$h(t)$は単調減少。

この時の生存関数は$S(t)=\color{red}{e^{-(\lambda t)^p}}$であり,

ハザード関数は,今生きている者のうち,単位時間後に死ぬ者の率であり,治療しない者は増加関数で,手術した者は減少関数で表せられる。

　　

〇肺結核などの慢性疾患を持つ人に対するモデルの場合

生存時間$T$が対数正規分布に従い,$\log T \sim N(\mu,\sigma^2)$とする。

$T$の確率密度関数：$f(t)=(\sqrt{2\pi}\sigma t)^{-1}e^{-(\log{t-\mu})^2/(2\sigma^2)}$

生存関数：$S(t)=\color{red}{1-\Phi\Big[{\displaystyle\frac{(\log{t-\mu})}{\sigma}}\Big]}$

ただし$\Phi(\cdot)$は標準正規分布の確率密度関数。

ハザード関数：$h(t)=\color{red}{-S'(t)/S(t)}$であり,増加から減少に転じるため,慢性疾患を持つ患者に適切なモデルである。

VI.比例ハザードモデル

〇白血病患者の死亡をイベントとした場合

治療効果のほか,予後因子として患者の白血球数などの複数の共変量$x$を考慮する必要がある。ハザード関数を用いた通常のモデルでは,

$$
h(t;x)=\exp(\alpha+x^\top\beta)=h_0e^{x^\top\beta} \quad,\quad (h_0=e^\alpha>0)
$$

　　
となり,時間に依存せず,生存時間$T$の分布は指数分布に限られる。確率密度関数$f(t)=\lambda \exp(-\lambda t)$をもつ指数分布のハザードは$\lambda$なので,$\lambda=h_0e^{x^\top\beta}$として。最尤法で$\alpha,\beta$を推定できる。

上記のモデルにおける$h_0$を$h_0(t)$で置き換えて得られたモデルをCox比例ハザードモデルという。

$$
h(t;x)=\color{red}{h_0(t)e^{x^\top\beta}\quad (h_0(t)>0)}
$$

$h_0(t)$は$h(t;x=0)$とあらわすことができ,基準ハザードと呼ぶが,例えば白血病の場合,「白血病でない人のもともとのハザード」などがこれに当てはまる。

また,生存時間がどのような分布にあっても採用することができる利点がある。

比例ハザードモデルでは,「ハザードを求めず,2群のハザード比だけを求めよう」という考えに基づくため,以下の式を定める。

となり,ハザード比は時間に依存しないことがわかり,これを比例ハザード性という。

比例ハザード性を確認するために,比例ハザードモデルのもとで,

$$
\log(-\log S(t;x))=\color{red}{x^\top\beta+\log H_0(t)}
$$

$$
H_0(t)=\color{red}{\int^t_0h_0(u)du}
$$

を導く。$H_0(t)$は基準累積ハザードといい,時間$t$までの基準ハザードの累積値をあらわす。

VII.カプラン・マイヤー推定量

パラメトリック・モデルの適用が難しい場合,生存関数の推定量を次のように構成できる。大きさ$n$の無作為標本$t_1,...,t_n$に対して,まず打ち切りが無い場合を考える。

$S(t)=1-F(t)$により,経験分布$F_n(t)$を用いて,

$$
\hat S(t)=1-F_n(t)=\color{red}{\frac{1}{n}\sum^n_{i=1}I(t_i>t)}
$$

で推定できる。ただし,$I(\cdot)$は定義関数である。推定量$\hat S(t)$はカプラン・マイヤー推定量の特殊な場合である。タイが無ければ$\hat S(t)$は死亡時刻ごとに$1/n$ずつ減少する階段関数である。

　　

次に,右打ち切りが伴う場合を考える。ある病気の手術を行ったあと死亡するまでの生存時間を分析する場合,患者の転院などの理由で生存時間が打ち切られることがある。

$n$人の患者を観察し始めたとして,時刻$t>0$までに時刻$0<t_1<t_2<...<t_k<t$で死亡が観測されたとする。

　　

時刻$t_i$での死亡数を$d_i$とする。また,「時刻$t_i$より前までは生存していたことがわかっている人数」を$n_i$とする。

$n_i$：最初の$n$人から時刻$t_i$より前に死亡した人数及び右打ち切りされた人数を引いた人数。

このとき,カプラン・マイヤー推定量は,

で与えられる。

時刻$t_j$におけるカプラン・マイヤー推定量は,直前の時刻$t_{j-1}$における推定量と,$t_j$までに生きていた条件の下での$t_j$を乗り越える条件付確率の推定量との積で表すことができ,

$\hat S(t_j)=\hat S(t_{j-1})\times\hat P[T>t_j|T \geq t_j]$が成立する。

これにより,カプラン・マイヤー推定量は,

$$
\hat S(t_j)=\color{red}{\prod^j_{i=1}\hat P[T>t_i|T\geq t_i]}
$$

として,条件付き生存確率の積で表現できることがわかる。

VIII.ニューラルネットワークモデル（未学習）

第２１章　標本調査法

単純無作為抽出法

大きさ$N$の母集団から,大きさ$n$の標本を非復元単純無作為抽出するとき,

変量$x_i$に対して,期待値は$E[\bar{x}]=\mu$,分散は,有限修正を用いて,

$$
V[\bar{x}]=\color{red}{\frac{N-n}{N-1}\cdot\frac{1}{n}\sigma^2}
$$

であらわされる。

母集団が無限母集団の場合や,有限抽出の場合は,有限修正項は用いない。

上記の推定量の分散を$c$以下に抑えたい場合,標本の大きさを求める公式は,単純に式変形することで

$$
n\geq \color{red}{\frac{N\sigma^2}{\sigma^2+(N-1)c}}
$$

となる。

層化抽出法

大きさ$N$の母集団を$L$個の層に分け,各層の大きさを$N_h(h=1,2,..,L)$とする。層$h$から大きさ$n_h$の標本を非復元無作為抽出して,その変量を$x_{hi}(i=1,2,..,n_h)$とする。このような抽出法を層化無作為抽出法という。

母平均$\mu$の推定量は,

$$
E[\bar{X}_{st}]=\mu
$$

また,推定量の分散は,$\sigma_h^2$を第$h$層の母分散として,

無限母集団や,復元抽出の場合は,

ネイマン分配法

標本分配法では,比例分配法,等分配法のほかに,推定量の分散を最小にするネイマン分配法があり,

層$h$の標本の大きさは,

$$
n_h=\color{red}{\frac{N_h \cdot \sigma_h \cdot \sqrt{\frac{N_h}{N_h-1}}}{{\displaystyle\sum^L_{h=1}}N_h \cdot \sigma_h \cdot \sqrt{\frac{N_h}{N_h-1}}} \times{n}}
$$

有限修正でない場合は,

$$
n_h=\color{red}{\frac{N_h \cdot \sigma_h}{{\displaystyle\sum^L_{h=1}}N_h \cdot \sigma_h} \times{n}}
$$

比例分配：大きい層から大きい標本を抽出する。

ネイマン分配：散らばりの大きい層からも大きい標本を抽出する。

第２２章　主成分分析

行列$X$を考える：$x_{ij}$：個体（人など）$i$で変数（身長など）$j$の値

係数は条件${\displaystyle\sum^p_{j=1}}w_{ij}^2=1$のもと,$y={\displaystyle\sum^p_{j=1}}w_jx_j$の分散を最大にする。その時の分散は$V(y)$で表す。

主成分分析における基本事項

〇固有値$\lambda_j$：新しい変数（総合特性）の$\color{red}{\mbox{分散}}$

$$\lambda_j=V(y_j)$$

ただし,$n^*=(n\quad or\quad n-1)$,$s_{jk}$：$x_j$の分散共分散行列。また$k$は新しい変数。

分散共分散行列は,標本相関行列に変えて表されることもある。

なお,主成分の分散の合計は,元の変数の分散の合計と等しい:$V(y)=V(x)$

そして,異なる主成分は無相関。

　　

〇固有ベクトル$w_j$：線形結合の式の$\color{red}{\mbox{係数}}$

　　

〇主成分負荷量$f_jk$：新しい変数への元の変数の寄与＝元の変数と主成分の相関係数

$$
f_jk=\frac{Cov(y_j,x_k)}{\sqrt{V(y_j)}\sqrt{V(x_k)}}=\color{red}{\frac{\sqrt{\lambda_j}}{s_k}w_{jk}}
$$

ここで,分析に相関行列が使われていた時,上記の分母のような標準化はすでにされているので,

主成分負荷量は,$[\color{red}{\sqrt{\lambda_j}u_{k,j}}\color{black}{]}$となる。

　　

〇寄与率$c_j$：主成分の持つ情報の割合

$c_j=\color{red}{\frac{\lambda_j}{\lambda_1+\lambda_2+...+\lambda_p}}$

累積寄与率$QC_k=\sum^k_{j=1}c_j$

　　

〇主成分スコア（得点）：新しい変数での値

例えば,個体$i$の変数$k$における主成分得点は,個体$i$のそれぞれの値を代入して,

$y_{ik}=w_{k1}x_{i1}+w_{k2}x_{i2}+...+w_{kp}x_{ip}$で求まる。

　　

〇第２３章の判別分析とSVMに関しては,導出や意味を理解すべきところであり,具体的な公式等は本資料では扱わない。

第２７章　時系列解析

I.平均・分散・自己共分散

期間$t=1,2,...,T$で観測される時系列データを$Y_1,Y_2,...,Y_T$とする。観測時点を固定した$Y_t$は各々確率変数となり,平均や分散を求めることができる。一般に,平均や分散は観測時点$t$に依存するので,

$$
E[Y_t]=\mu_t,\quad V[Y_t]=\sigma^2_t
$$

のように表記される。また,$Y_t$と$Y_{t-1}$のように,同一データの異なる地点の共分散を自己共分散,相関関係を自己相関関係と呼ぶ。時間差$h$をラグとすると,それぞれ

$$
Cov[Y_t,Y_{t-h}]=\gamma_{t,h} \
\rho[Y_t,Y_{t-h}]=\frac{Cov[Y_t,Y_{t-h}]}{\sqrt{V[Y_t]V[Y_{t-h}]}}=\rho_{t,h}
$$

で表せる。

II.定常性

時系列データの平均と分散が有限で,平均が観測地点$t$には依存せずに時間差$h$のみに依存する場合,その系列は,共分散定常過程もしくは弱定常過程という。

このとき,以下が成り立つ。

$\gamma_{|h|}$は$\rho_{|h|}$と表されることもある。

　　

一方,任意の整数$h_1,h_2,...,h_n$に対して,$Y_t,Y_{t-h_1},Y_{t-h_2},...,Y_{t-h_n}$の同時分布が時点$t$には依存せず,時間差$h_1,h_2,...,h_n$のみに依存する場合,$Y_t$は強定常過程と呼ばれる。

ホワイトノイズ：共分散定常過程の平均が$0$,$h \neq0$のすべての自己共分散が$0$である場合,その系列をホワイトノイズという。

III.自己回帰過程（AR過程）

AR(1)過程は以下のように表現できる。

$$
Y_t=c+\phi_1 Y_{t-1}+U_t
$$

$U_t$：系列$Y_t$を生成するショックと呼ばれ,ホワイトノイズと仮定される。

$$
\begin{split}
Y_t &= c+\phi_1Y_{t-1}+U_t\
&=c+\phi_1(\phi_1Y_{t-2}+U_{t-1})+U_t\
&=c+{\phi_1}^2Y_{t-2}+\phi_1U_{t-1}+U_t
\end{split}
$$

$|\phi_1|<1$のとき,過去から現在への影響は,時間差が開くほど弱くなり,AR(1)過程は共分散定常となる。

共分散定常の$Y_t$における

分散：$$\gamma_0=\color{red}{{\phi_1}^2\gamma_0+\sigma^2}$$

1次の自己共分散：$$\gamma_1=\color{red}{\phi\frac{\sigma^2}{1-{\phi_1}^2}}$$

h次の自己共分散：$$\gamma_h=\color{red}{{\phi_1}^h\frac{\sigma^2}{1-\sigma^2_1}}$$

h次の自己相関係数：$$\rho_h=\color{red}{{\phi_1}^h}$$

AR(1)過程は以下のように表現できる。

$$
Y_t=c+\phi_1Y_{t-1}+\phi_2Y_{t-2}+\cdot\cdot\cdot+\phi_pY_{t-p}+U_t
$$

IV.移動平均過程（MA過程）

$y_t$と$y_{t-1}$が共通成分を持っている場合のモデル。

MA(1)過程：

$$
Y_t=\mu+U_t+\theta_1U_{t-1}
$$

自己共分散（分散も含む）：

MA(p)過程：

$$
Y_t=\mu+U_t+\theta_1U_{t-1}+\theta_2U_{t-2}+\cdot\cdot\cdot+\theta_qU_{t-q}
$$

自己共分散：

V.自己回帰移動平均過程（ARMA過程）

AR過程とMA過程を組み合わせた(p,q)次の自己回帰移動平均過程：

$$
Y_t=c+\phi_1Y_{t-1}+\cdot\cdot\cdot+\phi_pY_{t-p}+U_t+\theta_1U_{t-1}+\cdot\cdot\cdot+\theta_qU_{t-q}
$$

階差を$\Delta Y_t=Y_t-Y_{t-1}$とすると,

(p,1,q)次の自己回帰和分移動平均過程（ARIMA過程）が以下のように得られる。

$$
\Delta Y_t=\phi_1\Delta Y_{t-1}+\cdot\cdot\cdot+\phi_p\Delta Y_{t-p}+U_t+\theta_1U_{t-1}+\cdot\cdot\cdot+\theta_qU_{t-q}
$$

$|\phi_1|=1$のとき,時点$t$からどの時間差においても過去からの影響があり,非定常性をもつ。

よって,階差をとるか取らないかを検定する方法として,$\phi_1=1$を帰無仮説とする単位根検定がある。

$\phi_1=1$の場合をとくにディッキー・フラー検定と呼ぶ。

　　

〇$AR(p)$過程の場合

$\rho=\phi_1+\cdot\cdot\cdot+\phi_p-1,\psi_j=-{\displaystyle\sum^p_{k=j+1}}\phi_k(j=1,2,...,p-1)$として,

$AR(p)$過程を以下のように書き換える。

$$
\Delta Y_t=c+\rho Y_{t-1}+\psi_1\Delta Y_{t-1}+\cdot\cdot\cdot+\psi_{p-1}\Delta Y_{t-p-1}+U_t
$$

共分散定常の条件は$\rho=0$なので,それを帰無仮説,$\rho<0$を対立仮説として$t$検定を行う。

VI.次数の決定

自己相関係数	偏自己相関係数	選択モデル
２次以降０	ゆっくりと減衰	MA(1)
３次以降０	ゆっくりと減衰	MA(2)
ゆっくりと減衰	２次以降０	AR(1)
ゆっくりと減衰	3次以降０	AR(2)
ゆっくりと減衰	ゆっくりと減衰	ARMA(1,1)

IIV.ダービン・ワトソン検定

以下の回帰モデルを考える。

$$
Y_t=\beta_1+\beta_2 X_{2t}+\cdot\cdot\cdot+\beta_K X_{Kt}+U_t
$$

ここで,誤差項$U_t$がホワイトノイズではなく,自己共分散が０ではない場合,誤差項には自己相関もしくは系列相関があると言われ,誤差項に自己相関があるかどうかの仮説検定としては,ダービン・ワトソン検定がある。

DW検定では,誤差項にAR(1)モデルを想定する。

$$
U_t=\rho U_{t-1}+\varepsilon_t
$$

ただし,$\varepsilon_t$はホワイトノイズ。$U_t$は$\rho=0$の場合にホワイトノイズとなるので,$0 \leq \rho \leq 1$のとき,ダービン・ワトソン検定では帰無仮説と対立仮説を,

$$
H_0:\rho=0\quad vs.\quad H_1:\rho>0
$$

とする。

最初のモデルを最小二乗法で推定し,得られた残差$\hat U_t$について,ダービン・ワトソン比を検定統計量として用いる。

$$
DW=\color{red}{\frac{\sum^T_{t=2}(\hat U_t-\hat U_{t-1})^2}{\sum^T_{t=1}\hat {U_t}^2}}
$$

ここで,$T$が十分大きいものであるとし,$\hat \gamma_1={\displaystyle\sum^T_{t=2}}\hat U_t \hat U_{t-1}\Big/{\displaystyle\sum^T_{t=1}{\hat U_t}^2}$とすると,

以下のように近似してあらわせる。

$$
DW\approx \color{red}{2(1-\hat \gamma_1)}
$$

よって,

$$
\begin{split}
\rho=0 \Longleftrightarrow \hat\gamma_1 \approx0 \Longleftrightarrow DW \approx 2\
\rho>0 \Longleftrightarrow \hat\gamma_1 >0 \Longleftrightarrow DW < 2
\end{split}
$$

となり,DW比の値が２に近いときに帰無仮説を受容し,２より十分小さなときに帰無仮説を棄却する。

第２８章　分割表

分割表の例

因子：処方薬＆改善度

水準：（新薬,従来薬）と（効果あり,効果なし）

	効果あり	効果なし	計
新薬	16	4	20
従来薬	12	8	20
計	28	12	40

議論を一般化して,処方薬が新薬,従来薬である事象を$A_1,A_2$,改善度が効果あり,効果なしであるという事象を$B_1,B_2$とする。

各群$A_i$の事象$B_1$の頻度を$x_i$,標本サイズを$n_i$とし,効果ありである二項確率を$\theta_1,\theta_2$とする。

この時,生起確率の違いを検証したいので,帰無仮説と対立仮説を

$$
H_0:\theta_1=\theta_2\quad vs. \quad H_1:\theta_1 \neq \theta_2
$$

として考える。

I.オッズ比

２つの二項確率$\theta_1,\theta_2$について,${\displaystyle\frac{\theta_1}{(1-\theta_1)}},{\displaystyle\frac{\theta_2}{(1-\theta_2)}}$をそれらのオッズと呼び,

　　

それらの比$\psi=\color{red}{{\displaystyle\frac{\theta_1/(1-\theta_1)}{\theta_2/(1-\theta_2)}}}$をオッズ比と呼ぶ。その対数$\log \psi$を対数オッズ比という。

　　

実際に標本を用いて計算されたオッズ比を標本オッズ比と呼び,$OR$で表す。

II.前向き研究と後向き研究

前向き研究：

新薬と従来薬を一定数用意した後で,一定時間後に効果があるかないかを調べる手順。

後向き研究：

効果があったものと無かったもののデータを先に抽出してから,それらが新薬であったか従来薬であったかを調査する手順。

　　

前向き後向きのどちらにおいても上記のオッズ比は一致し,二項確率$\theta_1,\theta_2$が十分小さい場合には,

$$
\psi={\displaystyle\frac{\theta_1/(1-\theta_1)}{\theta_2/(1-\theta_2)}}\approx\color{red}{\frac{\theta_1}{\theta_2}}
$$

とくに,注目している事象$B_1$が有害事象である場合に,相対リスクと呼ばれる。

III.母数の推定

母数$\theta_i$の自然な点推定値は,

$$
\hat\theta_i=\color{red}{\frac{x_i}{n_i}}
$$

であることから,上記のオッズ比$\psi$を推定する場合,標本オッズ比である

$$
OR=\color{red}{\frac{x_1(n_2-x_2)}{x_2(n_1-x_1)}}
$$

を用いる。標本サイズが十分大きいとき,標本オッズ比の対数（標本対数オッズ比）の推定誤差は,

$$
\color{red}{\sqrt{\frac{1}{x_1}+\frac{1}{n_1-x_1}+\frac{1}{x_2}+\frac{1}{n_2-x_2}}}
$$

で近似される。

IV.適合度カイ二乗検定＆尤度比検定

当てはめ値：

各セル頻度の期待値のこと。

冒頭の値をさらに扱いやすくするために,分割表を以下のように書き換える。

観測値(母数)	$B_1$	$B_2$	計
$A_1$	$x_{11}(\theta_{11})$	$x_{12}(\theta_{12})$	$x_{1\cdot}(\theta_{1\cdot})$
$A_2$	$x_{21}(\theta_{21})$	$x_{22}(\theta_{22})$	$x_{2\cdot}(\theta_{2\cdot})$
計	$x_{\cdot 1}(\theta_{\cdot 1})$	$x_{\cdot 2}(\theta_{\cdot 2})$	$x_{\cdot \cdot}(\theta_{\cdot \cdot})$

このとき,当てはめ値$m=(m_{ij})$は,

$$
m_{ij}=\color{red}{\frac{x_{i\cdot}x_{\cdot j}}{x_{\cdot\cdot}}}
$$

であり,標本オッズ比,標本対数オッズ比の標準誤差の近似値は,

$$
\begin{split}
OR&=\color{red}{\frac{x_{11}x_{22}}{x_{12}x_{21}}}, \
\sqrt{V[\log OR]} &\approx \color{red}{\sqrt{\frac{1}{x_{11}}+\frac{1}{x_{12}}+\frac{1}{x_{21}}+\frac{1}{x_{22}}}}
\end{split}
$$
となる。

　　

〇適合度カイ二乗検定

適合度カイ二乗検定の検定統計量は,

$$
\chi^2=\color{red}{\sum_i \sum_j \frac{(x_{ij}-m_{ij})^2}{m_{ij}}}
$$

で定義される。$2 \times 2$分割表では,これを式変形した,

$$
\chi^2=\color{red}{\frac{x_{\cdot\cdot}(x_{11}x_{22}-x_{12}x_{21})^2}{x_{1\cdot}x_{2\cdot}x_{\cdot 1}x_{\cdot 2}}}
$$

とも表現され,帰無仮説が正しいとき,$\chi^2$は自由度$1$のカイ二乗分布に従う。

　　

〇尤度比検定

尤度比検定統計量$\Lambda$に対して,$G^2=2 \log \Lambda$が漸近的にカイ二乗分布に従うことを利用して検定を行う。この値は逸脱度と呼ばれる。

母数の最尤推定量を代入することで,

$$
G^2=2 \log \Lambda=\color{red}{2 \sum_i \sum_j x_{ij} \log\frac{x_{ij}}{m_{ij}}}
$$

V.フィッシャーの正確検定

〇条件付分布に基づく条件付検定の手法

考える仮説はオッズ比$\psi={\displaystyle\frac{\theta_{11}\theta_{22}}{\theta_{12}\theta_{21}}}$についての片側検定

$$
H_0:\psi=1 \quad vs. \quad H_1:\psi>1
$$

$x_{ij}$のうち,任意の１つの値を定めれば残りの３つの値はすべて定まる。ここでは$x_{11}$に注目する。

例えば,$(A_1,B_1)$を,「新薬で効果あり」のセルであるとすると,$x_{11}$に関する超幾何分布の確率関数として考えることができ,

その値は

$$
P(X_{11}=x_{11})=\color{red}{\frac{x_{1\cdot}!x_{2\cdot}!x_{\cdot1}!x_{\cdot2}!}{x_{\cdot\cdot}!}\cdot\frac{1}{x_{11}!x_{12}!x_{21}!x_{22}!}}, \quad x_{11}x_{12}x_{21}x_{22} \geq 0
$$

$x_{11}$がとりうる値の範囲は,

$$
\color{red}{\max{0\quad,\quad x_{1\cdot}+x_{\cdot1}-x_{\cdot\cdot}} \leq x_{11} \leq \min{x_{1\cdot}\quad,\quad x_{\cdot}1 }}
$$

として表すことができる。後者が見にくいので例を挙げると,

$$
\color{red}{\max{0\quad,\quad \mbox{当該行列の総和}-\mbox{全体の総和} } \leq x_{11} \leq \min{\mbox{当該行と列の部分和の小さいほう} }}
$$

$$
\color{red}{\max{0\quad,\quad 7+9-14} \leq x_{11} \leq \min{7\quad,\quad 9 }}
$$

これを用いて,P値は以下のように表せる。

$$
P(X_{11}\geq x_{11})=\color{red}{\sum_{x\geq x_{11}}P(X_{11}=x)}
$$

また,対立仮説が逆向き$H_1:\psi<1$のときは,

$$
P(X_{11}\leq x_{11})=\color{red}{\sum_{x\leq x_{11}}P(X_{11}=x)}
$$

第２９章　不完全データの統計処理

欠測：

アンケートの回答拒否や測定器具の不具合などにより,データが観測されないこと。

　　

欠測メカニズム：

データが２種類あり,観測データ（すべての個体において観測できたデータ）を$x$,欠測データ（欠測が含まれるデータ）を$y$とする。

完全にすべてのデータが観測されたものをCompleteとする。

　　

(a)MCAR：欠測は,欠測データ及び観測データの両方に依存せず,ランダムに生じる。

ランダムに欠測が生じるので,各種統計量がCompleteと似たものになりやすい。

　　

(b)MAR：欠測は,観測データに依存して生じるが,欠測データの値にはよらない。

例えば$x$の値が大きいものに欠測が生じたとき,２変量の相関が正の場合,欠測する$y$も大きな値となりやすく,Completeと比べて,$\color{red}{\mbox{平均と標準偏差が小さくなりやすい}}$。

　　

(c)MNAR：欠測は,欠測データそのものの値に依存して生じる。

$y$の大きな値が欠測となるため,$y$の**$\color{red}{\mbox{平均と標準偏差が小さく}}$**なり,回帰直線のパラメータも影響を受ける。

I.削除法と補完法

CC解析：

多変量データで１か所でも欠測のある個体は個体ごと削除し,すべての変量が観測されている個体のみを用いる解析法。

MARの場合,正の相関があると,$x$の**$\color{red}{\mbox{平均及び標準偏差が過小評価}}$**となる。

　　

AC解析：

ある変量の投機量の計算は別の変量とは無関係であることから,当該変量の使えるデータはすべて使うという解析手法。欠測に関しては,以下の補完法を使う。

(i) 平均値代入：当該変量の観測データのみから求めた平均値を代入。

MARでは,欠測してないデータから求めた平均が適用されるが,平均の過小評価が解消されないだけでなく,平均データを増やしたことで**$\color{red}{\mbox{標準偏差がさらに過小評価}}$**となる。

(ii) 回帰代入：回帰式によって欠測部分を予測して代入。

MARでは,平均の過小評価が解消されるが,回帰代入では$y$方向のバラツキが考慮されないため,標準偏差は過小評価のままであり,**$\color{red}{\mbox{相関係数はむしろ過大評価}}$**となる。

(iii) HotDeck法：欠測のある個体と似た個体を同じデータセットから探して代入。

(i)(ii)場合において,MCARでは平均には影響を及ぼさないが,標準偏差の過小評価を招くので,補完する必要はない。

MNARの場合は,いずれの対処法もよい結果を与えるという保証がなく,欠測となった理由ごとの個別対応が必要となる。

II.正規分布における推測

１変量正規分布

〇平均値の推測

$c$以下のデータは観測されるが,$c$を超えると観測されなくなるとする。また,データは全部で$n$個あるとする。

観測されないデータ数がわかっている場合を打ち切りといい,観測されたデータ数を$m$,それ以外が$n-m$個あるとする。

観測されないデータ数がわかっていない場合をトランケートという。

$a^{(t)}={\displaystyle\frac{c-\mu^{(t)}}{\sigma}}$,$\varphi(\cdot)$を$N(0,1)$の確率密度関数,$\Phi(\cdot)$を$N(0,1)$の累積分布関数とする。

初期値$\mu^{(0)}$を出発点とすると,反復のEMアルゴリズムによって,平均の推測値はそれぞれ以下のようにあらわせる。

〇打ち切り

$$
\mu^{(t+1)}=\color{red}{\frac{1}{n}\Biggl(\sum^m_{i=1}x_i+(n-m)\biggl(\mu^{(t)}+\frac{\varphi(a^{(t)})}{1-\Phi(a^{(t)})}\sigma \biggl) \Biggl)}
$$

〇トランケーション

$\bar x=(x_1+...+x_m)/m$として,

$$
\mu^{(t+1)}=\color{red}{\bar x+\frac{\varphi(a^{(t)})}{\Phi(a^{(t)})}\sigma}
$$

２変量正規分布

２変量確率関数$(X,Y)$は２変量正規分布に従うとし,２変量データ$(x,y)$のうち,$x$はすべて観測され,$y$に欠測が発生したとする。この時の観測データを,

$(x_1,y_1),...,(x_m,y_m),x_{m+1},...,x_n$とすると,

$x$はすべて観測されていることから,$x$の周辺分布に関するパラメータ$\mu_X$と${\sigma_X}^2$の最尤推定値は,$n$個のデータをもとに

$$
\begin{split}
\hat\mu_X&=\color{red}{\frac{1}{n}\sum^n_{i=1}x_i},\
{\hat\sigma_X}^2&=\color{red}{\frac{1}{n}\sum^n_{i=1}(x_i-\bar x)^2}
\end{split}
$$

と表せる（標本分散の除数は$n-1$なのに対し,最尤推定の場合は$n$である）。

２変量とも観測された$m$組に関する統計量について,

$$
\begin{split}
\bar x=\frac{1}{m}\sum^m_{i=1}x_i,\quad {s_X}^2=\frac{1}{m}\sum^m_{i=1}(x_i-\bar x)^2\
\bar y=\frac{1}{m}\sum^m_{i=1}y_i,\quad {s_Y}^2=\frac{1}{m}\sum^m_{i=1}(y_i-\bar y)^2\
s_{XY}=\frac{1}{m}\sum^m_{i=1}(x_i-\bar x)(y_i-\bar y),\quad r=\frac{s_{XY}}{s_xs_Y}
\end{split}
$$

とする。

また,$x$から$y$を予測するための回帰式を$y=\alpha+\beta x$とし,その際の誤差分散を$\tau^2$とする。

これらを用いて,回帰パラメータ及び誤差分散の最尤推定値は以下のようにあらわせる。

$$
\begin{split}
\hat\alpha&=a=\color{red}{\bar y-b\bar x}\
\hat\beta&=b=\color{red}{\frac{s_{XY}}{s_{X^2}}}\
\hat\tau^2&=\color{red}{{s_{Y}}^2-\frac{s_{XY^2}}{s_{X^2}}}
\end{split}
$$

ここで,真の値を用いたパラメータの関係式は,

$$
\mu_Y=\alpha+\beta\mu_X,\quad {\sigma_Y}^2=\tau^2+\beta^2{\sigma_X}^2,\quad \sigma_{XY}=\beta{\sigma_X}^2
$$

によってあらわせるので,上記の最尤推定値を用いて,

$$
\begin{split}
\hat\mu_Y&=\color{red}{\hat\alpha+\hat\beta\hat\mu_X},\
{\hat\sigma_Y}^2&=\color{red}{\hat\tau^2+\hat\beta^2{\hat\sigma_X}^2},\
\hat\sigma_{XY}&=\color{red}{\hat\beta{\hat\sigma_X}^2},\
\hat\rho&=\color{red}{\frac{\hat\sigma_{XY}}{\hat\sigma_X\hat\sigma_Y}}
\end{split}
$$

となる。

第３０章　モデル選択

I.赤池情報量基準（AIC）

情報量基準：

すべての変数を用いるのではなく,何らかの基準に基づき,適切な変数を選択したい場合に,尤度とパラメータの数に基づいて変数選択をする際に使う基準

そのモデルにおける最大尤度（パラメータを最尤推定したときの尤度）を$L$,推定するパラメータ数を$k$とおくと,

$$
AIC=\color{red}{-2\log L+2k}
$$

で計算される。統計モデルの候補の中で,AICの値を最小にするモデルを選ぶ。

II.ベイズ情報量基準（BIC）

$$
BIC=\color{red}{-2\log L+k\log n}
$$

AICと比較すると,推定するパラメータの数によるペナルティが$2k$から$\log k$に変わっているため,$n \geq 8$のとき,BICの方がより簡潔なモデルを選ぶ（データ数が$n=e^2$以上になるとより厳しく判定）。

「BIC は，有意なパラメータと，そうでないものとが，容易に識別できる状況に対応するモデルから得られ，これに対してAICは，有意性がようやく認められる程度のパラメータの取り扱いに注目し，誤差の影響に埋没しそうになるところまでモデル化の可能性を追及」（赤池1996）

III.クロスバリデーション（交差検証法）

学習データとテストデータを分けることで過剰評価を防ぐ。この時,全体のデータを２分割し,片方のデータセットで判別関数を求め,残しておいたもう片方のデータセットにその判別関数を適応して誤判別率を推定する。

とくに,$K=n$（$n$は標本の大きさ）とした場合のクロスバリデーションはLeave-one-out法と呼ばれる。

$K$通りのテストデータの選び方をし,他の$K-1$セットのデータで学習するものである。

その他の試験範囲

〇分散分析と実験計画法（第２０章）

別途,「分散分析実践」にてまとめてある。

〇クラスター分析（第２４章）

〇因子分析・グラフィカルモデル（第２５章）

因子分析,操作変数法,モラルグラフなど。

〇その他の多変量解析手法（第２６章）

多次元尺度法,正準相関分析,数量化法・対応分析など。

〇シミュレーション（第３２章）

モンテカルロ法,乱数生成,ジャックナイフ法・ブートストラップ法など。