光が媒質の境界で別の媒質側へ進むとき,光の進行方向が変わる現象が起こり,これを屈折と呼びます.
光がある媒質を透過する速度を $v$ とするとき,真空中の光速 $c$ と媒質中の光速との比は
\eta = \frac{c}{v}
となります.この $\eta$ がその媒質の屈折率です.
入射角と屈折角の関係は,屈折前の媒質の屈折率 $\eta_{1}$ と,屈折後の媒質の屈折率 $\eta_{2}$ からスネルの法則(Snell's law)を用いて計算することができます.
\eta_{1} \sin\theta_{1} = \eta_{2} \sin\theta_{2}
$\theta_{2}$ は屈折角です.
スネルの法則
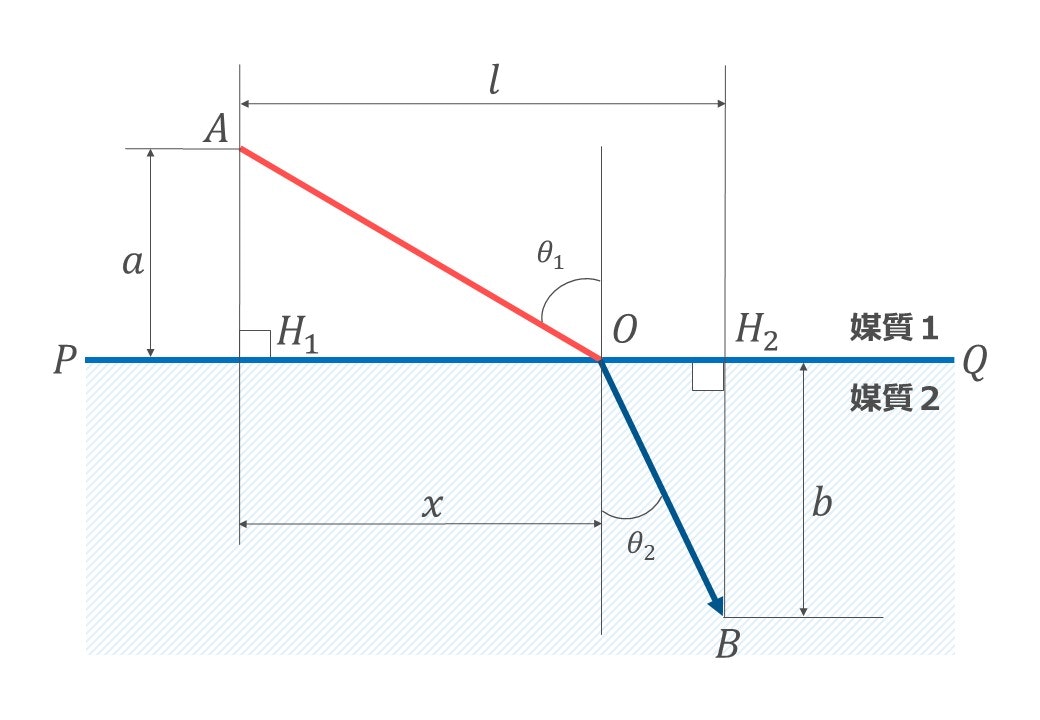
$PQ$ を媒質の境界として,媒質1内の点$A$から境界$PQ$上の点$O$に達して屈折し,媒質2内の点$B$に進むとします.
媒質1での光速を $v_{1}$,媒質2での光速を $v_{2}$,真空中の光速を $c$ とすれば
\begin{align}
\eta_{1} &= \frac{c}{v_{1}} \\[2ex]
\eta_{2} &= \frac{c}{v_{2}}
\end{align}
となります.
点$A$と点$B$から境界$PQ$に下ろした垂線の足を $H_{1}, H_{2}$ としたとき
\begin{align}
H_{1}H_{2} &= l \\[2ex]
AH_{1} &= a \\[2ex]
BH_{2} &= b
\end{align}
と定義します.
点$H_{1}$から点$O$までの距離を$x$として,この$x$を求めて点$O$の位置を特定します.
$AO$間を光が進むのにかかる時間は
t_{AO} = \frac{AO}{v_{1}} = \frac{\eta_{1}}{c}AO
また,$OB$間を光が進むのにかかる時間は
t_{OB} = \frac{OB}{v_{2}} = \frac{\eta_{2}}{c}OB
となります.したがって,光が$AOB$間を進むのにかかる時間は次のようになります.
t = t_{AO} + t_{OB} = \frac{1}{c}(\eta_{1}AO + \eta_{2}OB)
$AO$ と $OB$ はピタゴラスの定理から
\begin{align}
AO &= \sqrt{x^2+a^2} \\[2ex]
OB &= \sqrt{(l-x)^2+b^2}
\end{align}
だとわかります.整理すると次のようになります.
t = \frac{1}{c}(\eta_{1}\sqrt{x^2+a^2} + \eta_{2}\sqrt{(l-x)^2+b^2} \tag{1}
フェルマーの原理によると,「光が媒質中を進む経路は,その間を進行するのにかかる時間が最小となる経路である」といえます.
すなわち,光は$AOB$間を進むのにかかる時間$t$が最小となる経路を通ると考え,さきほどの式(1)の$t$が最小となるのは
\frac{dt}{dx} = 0
を満たすときです.式(1)を代入すると次のようになります.
\frac{dt}{dx} = \frac{d}{dx} \left\{ \frac{1}{c}(
\eta_{1}\sqrt{x^2+a^2} +
\eta_{2}\sqrt{(l-x)^2+b^2}
)
\right\} = 0
1/c は定数なので外に出せます.
\frac{dt}{dx} = \frac{1}{c} \left(
\eta_{1}\sqrt{x^2+a^2} +
\eta_{2}\sqrt{(l-x)^2+b^2}
\right)' = 0
和の微分ですので,$\eta_{1}$と$\eta_{2}$のある項をそれぞれ$x$で微分して足し合わせます.
\begin{align}
\eta_{1}\sqrt{x^2+a^2}'
&= \eta_{1} \frac{(x^2+a^2)'}{2\sqrt{x^2+a^2}} \\[2ex]
&= \eta_{1} \frac{2x}{2\sqrt{x^2+a^2}} \\[2ex]
&= \eta_{1} \frac{x}{\sqrt{x^2+a^2}} \\[2ex]
\eta_{2}\sqrt{(l-x)^2+b^2}'
&= \eta_{2} \frac{((l-x)^2+b^2)'}{2\sqrt{(l-x)^2+b^2}} \\[2ex]
&= \eta_{2} \frac{(l^2-2lx+x^2+b^2)'}{2\sqrt{(l-x)^2+b^2}} \\[2ex]
&= \eta_{2} \frac{-2(l-x)}{2\sqrt{(l-x)^2+b^2}} \\[2ex]
&= \eta_{2} \frac{-(l-x)}{\sqrt{(l-x)^2+b^2}}
\end{align}
整理すると
\frac{\eta_{1}}{c} \frac{
x
}{
\sqrt{
x^2 + a^2
}
} -
\frac{\eta_{2}}{c} \frac{
l-x
}{
\sqrt{
(l-x)^2 + b^2
}
} = 0
\tag{2}
図から $\sin\theta_{1}, \sin\theta_{2}$ を定義すると
\begin{align}
\sin\theta_{1} &= \frac{H_{1}O}{AO} = \frac{x}{\sqrt{x^2+a^2}} \\[2ex]
\sin\theta_{2} &= \frac{H_{2}O}{OB} = \frac{l-x}{\sqrt{(l-x)^2+b^2}}
\end{align}
となりますので,先ほどの式(2)を書き換えて,$c$ を両辺にかけて消すと
\eta_{1}\sin\theta_{1} = \eta_{2}\sin\theta_{2}
となります.これがスネルの法則の式です.
全反射
スネルの法則の式を変形して,
\sin\theta_{2} = \frac{\eta_{1}}{\eta_{2}} \sin\theta_{a} \tag{3}
とするとき,$\eta_{1} < \eta_{2}$ ならば,$\eta_{1}/\eta_{2} < 1$ となります.また,$0 < \sin\theta_{1} < 1$ であり,上記の式(3)から $\sin\theta_{2}$ は
0 < \sin\theta_{2} < 1
となりますから,式(3) を満たす屈折角 $\theta_{2}$ が必ず存在することになります.
逆に,$\eta_{1} > \eta_{2}$ の場合は,$\eta_{1}/\eta_{2} > 1$ なので,式(3) において,$\sin\theta_{1}$ が大きいと,$\sin\theta_{2} > 1$ となり解が得られない場合があります.入射角$\theta_{1}$ を次第に大きくしていくとき,
\sin\theta_{2} = 1
すなわち,屈折角 $\theta_{2}$ が $90^\circ$ となり,屈折光が発生しなくなる限界の入射角を $\theta_{c}$ とすれば,
\sin^{-1} \frac{\eta_{2}}{\eta_{1}}
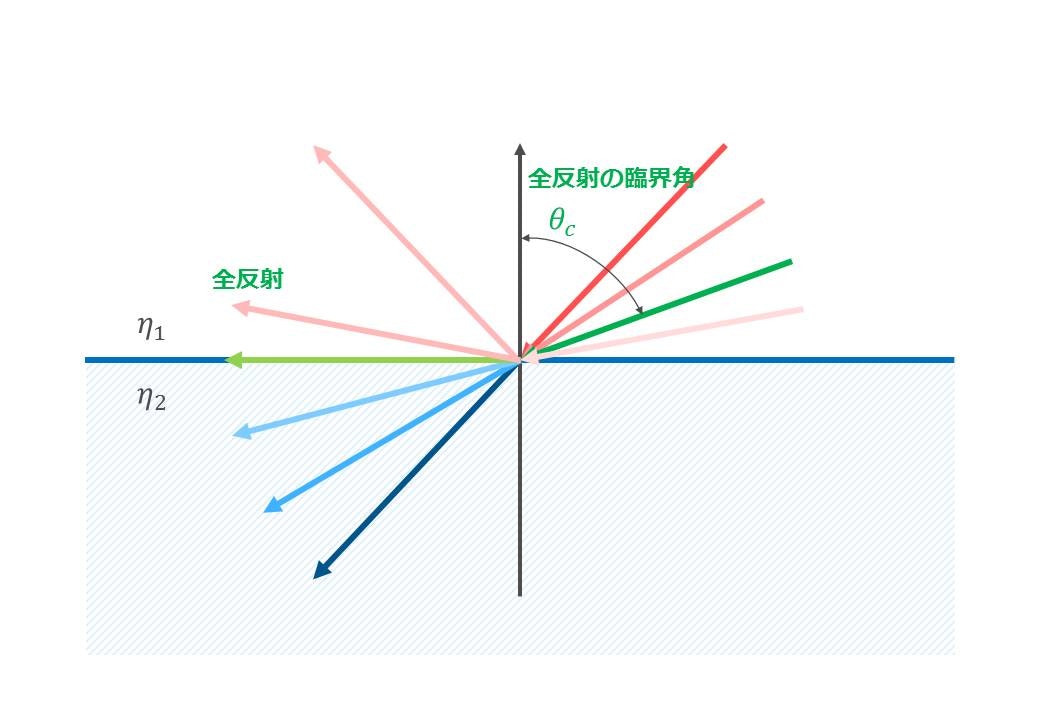
と表せます.下図のように入射角が$\theta_{c}$を超えると全部の光を反射します.これを全反射といいます.
また,この屈折光が発生しなくなる限界の入射角$\theta_{c}$を全反射の臨界角といいます.
屈折光の方向
屈折光の方向はスネルの法則を使って求めることができます.
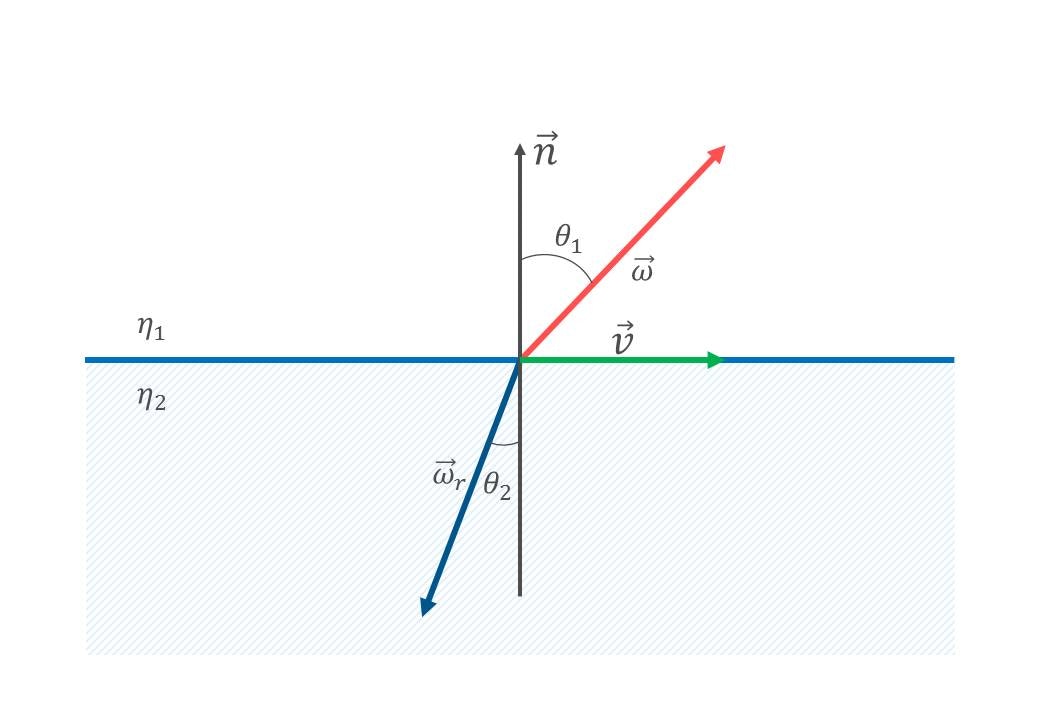
入射ベクトルと法線ベクトルを含む面があるとし,その面上で法線ベクトルと直交している単位ベクトルを$\vec{v}$とします.
この単位ベクトルと屈折ベクトル $\vec{\omega}_{r}$ の関係を表すと次のようになります.
\vec{\omega}_{r} = -\vec{v} \sin\theta_{2} -\vec{n} \cos\theta_{2}
入射ベクトルと法線ベクトルを使って,$\vec{v}$の関係を表すと
\vec{v} \sin\theta_{1} = \vec{\omega} - (\vec{\omega} \cdot \vec{n}) \vec{n}
これを先ほどの式に代入すると
\vec{\omega}_{r} = -\frac{
\vec{\omega} - (\vec{\omega} \cdot \vec{n}) \vec{n}
}{
\sin\theta_{1}
} \sin\theta_{2}
-\vec{n} \cos\theta_{2}
スネルの法則を使って$\sin\theta_{1}$を書き換えると
\begin{align}
\vec{\omega}_{r} &= -\frac{
\vec{\omega} - (\vec{\omega} \cdot \vec{n}) \vec{n}
}{
\frac{\eta_{2}}{\eta_{1}} \sin\theta_{2}
} \sin\theta_{2}
-\vec{n} \cos\theta_{2} \\[2ex]
&= -\frac{\eta_{1}}{\eta_{2}} \left(
\vec{\omega} - (\vec{\omega} \cdot \vec{n}) \vec{n}
\right)
-\vec{n} \cos\theta_{2}
\end{align}
次に $\cos\theta_{2}$ を変形していきます.まず $\cos^2\theta = 1-sin^2\theta$ を使って
\vec{\omega}_{r} =
-\frac{\eta_{1}}{\eta_{2}} \left(
\vec{\omega} - (\vec{\omega} \cdot \vec{n}) \vec{n}
\right)
-\vec{n} \sqrt{
1-\sin^2\theta_{2}
}
スネルの法則を使って $\sin^2\theta_{2}$ を $\sin^2\theta_{1}$ に変えます.
\vec{\omega}_{r} =
-\frac{\eta_{1}}{\eta_{2}} \left(
\vec{\omega} - (\vec{\omega} \cdot \vec{n}) \vec{n}
\right)
-\vec{n} \sqrt{
1-\left(
\frac{\eta_{1}}{\eta_{2}}
\right)^2 \sin^2\theta_{1}
}
そして,$\sin^2\theta_{1}$ を $1-\cos^2\theta_{1}$ に置き換えます.
\vec{\omega}_{r} =
-\frac{\eta_{1}}{\eta_{2}} \left(
\vec{\omega} - (\vec{\omega} \cdot \vec{n}) \vec{n}
\right)
-\vec{n} \sqrt{
1-\left(
\frac{\eta_{1}}{\eta_{2}}
\right)^2 (1-\cos^2\theta_{1})
}
$\cos\theta_{1}$ は入射ベクトルと法線ベクトルの内積で求まります.
\cos\theta_{1} = \vec{\omega} \cdot \vec{n}
これを代入すると
\vec{\omega}_{r} =
-\frac{\eta_{1}}{\eta_{2}} \left(
\vec{\omega} - (\vec{\omega} \cdot \vec{n}) \vec{n}
\right)
-\vec{n} \sqrt{
1-\left(
\frac{\eta_{1}}{\eta_{2}}
\right)^2 (1-(\vec{\omega} \cdot \vec{n})^2)
}
となります.これが屈折光の方向を計算する式です.