はじめまして、個人開発を主に活動しております maturu です。
突然ですが皆さんはスマートフォンで GPS ではなし得ない屋内位置情報アプリを開発したいと思ったことはありませんか？また、技術的・学術的興味から漠然とは理解しつつもどういった方法で屋内位置情報を特定するのか気になったことはありませんか？
近年の屋内位置情報を特定する方法として一般的なのは Wifi やビーコン、RFID などを建物や追跡対象(人や物)に設置させ、その電波強度の測定や三点測位を行い位置情報を割り出し、サーバーに転送して...といった風なものですが、これらの手法に共通しているのはインフラ整備が必要になるということです。つまり、莫大な導入コストがかかってしまうということですね。
そこで注目されているのが加速度センサーや地磁気センサー、角速度センサーを使用した歩行者自立航法測位(PDR)です。PDR 法は他の手法と比べ、インフラ整備をする必要がなく、容易な導入や大幅なコストカットができることが特徴です。中でも、2014 年に Wonho Kang と Youngnam Han らが提案したスマートフォンに組み込まれたセンサーを使用する SmartPDR は非常に高い精度で屋内位置を特定することに成功しています。
また現在、インドアマップなどの屋内位置情報を用いたアプリは各 OS に対応したネイティブ環境での開発が主流ですが、近年のスマホアプリの開発は React Native などのクロスプラットフォームフレームワークを利用したものが増加傾向にあります。
本記事では、そんな屋内位置情報を推定するための SmartPDR について具体的に解説し、React Native を用いて実現したものをご紹介します。
注意： 著者は React をつい最近始めた初心者です。ソースコードの不備などが多分に含まれている可能性があります。そのような部分を発見した場合は、コメントしていただけると幸いです。
GitHub: https://github.com/Firecommit/react-native-smartpdr
Paper: Kang, Wonho, and Youngnam Han. "SmartPDR: Smartphone-based pedestrian dead reckoning for indoor localization." IEEE Sensors journal 15.5 (2014): 2906-2916.URL
SmartPDR
PDR とは、一秒あたりの速度変化を測定する加速度センサー、回転角速度を測定するジャイロセンサー、磁場の大きさを測定する磁気センサーを複合的に活用し、歩行者の移動方向、移動距離、歩数を計算して相対的な現在地を推定するものです。通常、PDR は加速度センサによってステップイベントの数（歩数）を検出し、磁気センサーまたはジャイロセンサーによって移動方向が決定され、その方向にステップ長(歩幅)分だけ位置を移動させます。また、歩幅は歩行速度に合わせて平均歩幅が計算され、歩行者の現在地を測定するために使用されますが、より洗練されたシステムにおいては、加速度計の信号を分析した上でこれを推定します。SmartPDR は、これらの機能をスマートフォンに組み込まれたセンサーを使用してユーザーの動きを追跡するように、スマートフォン向けに特別に設計された歩行者の動きを追跡するモバイルアプリケーション用のミドルウェアです。
システム構造
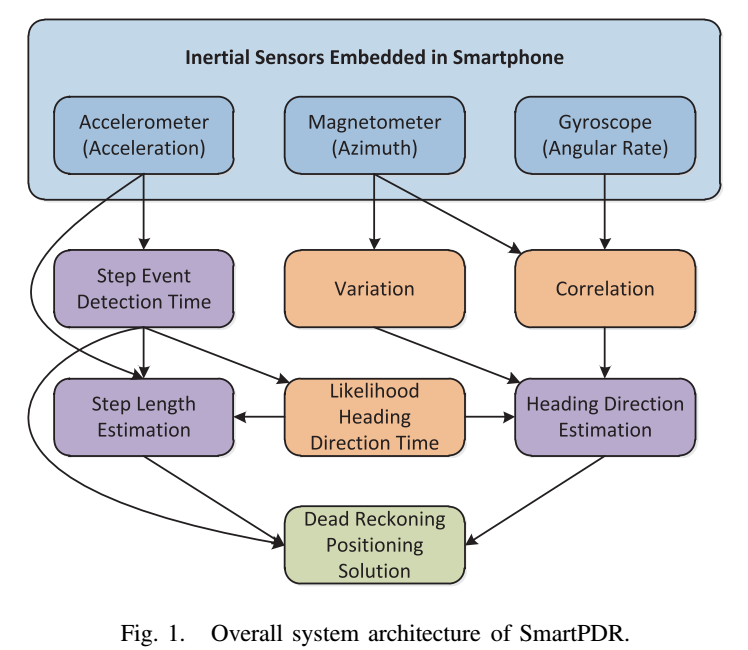SmartPDRは、ユーザーの動きを推定するために、3軸加速度センサーでステップイベントとステップ長を計算し、3軸磁力センサーと3軸ジャイロセンサーの両方で進行方向を決定します。このとき、磁力センサーとジャイロセンサーは相関関係にあり、さらに進行方向決定の際には磁力センサーをValidationとして使用します。最近のスマートフォンにはこれらのセンサーが標準搭載されているため、このようなアプローチはとても実用的です。既にスマートフォンが普及している現代社会においては、屋内測位の方法として非常に効果的だと言えますね。
システムは、ステップイベントが発火した時点で、進行方向以前のユーザーの位置にステップ長を追加することによって、次の位置を推定します。SmartPDR のコアプロセスは、ステップイベントの検出、進行方向の推定、ステップ長の推定、位置の推定の 4 ステップを繰り返します。
事前準備： 座標変換システム
回転行列
 |
 |
さて、コアプロセスについて説明する前に、ローカル座標系(LCS:Local Coordinate System)に関してグローバル座標系(GCS:Global Coordinate System)で任意の方向ベクトルのコンポーネントを記述するために、座標変換について簡単に説明しなければなりません。ここでのLCSはスマートフォンに組み込まれたそれぞれの3軸センサーにおける座標系のことで、GCSは地球の方位角と重力を表す座標系を示しています。
座標変換の詳細はこちら →http://www.mech.tohoku-gakuin.ac.jp/rde/contents/course/robotics/coordtrans.html
LCS から GCS の変換は、回転角をオイラー角として表すことができる LCS の 3 軸を中心とした連続回転と、その時間tにおける 3 軸に沿った回転行列を用いて実現できます。以下はその回転行列です。
R_{\phi, t} =
\begin{bmatrix}
\cos\phi_t & 0 & \sin\phi_t \\
0 & 1 & 0 \\
-\sin\phi_t & 0 & \cos\phi_t
\end{bmatrix}
\\
R_{\theta, t} =
\begin{bmatrix}
1 & 0 & 0 \\
0 & -\cos\theta_t & \sin\theta_t \\
0 & \sin\theta_t & \cos\theta_t
\end{bmatrix}
\\
R_{\psi, t} =
\begin{bmatrix}
\cos\psi_t & \sin\psi_t & 0 \\
-\sin\psi_t & \cos\psi_t & 0 \\
0 & 0 & 1
\end{bmatrix}\\
ここで、回転は$R_{\phi, t}$として示される$y$軸周りの$\phi_t$回転、$R_{\theta, t}$としての$x$軸周りの$\theta_t$回転、$R_{\psi, t}$としての$z$軸周りの$\psi_t$回転によって実行され、特にこれらの回転角度はそれぞれロール(Roll)、ピッチ(Pitch)、ヨー(Yaw)と呼ばれます。回転行列の行は実際には LCS 上の GCS の射影であり、列は GCS 上の LCS の射影です。ベクトルを LCS から GCS に変換する最終的な回転行列$R_t$は、これら 3 つの回転行列を順番に乗算することで得られます。
R_t = R_{\psi,t}R_{\theta, t}R_{\phi, t} \\
= \begin{bmatrix}
C_{\psi_t}C_{\phi_t}-S_{\psi_t}S_{\theta_t}S_{\phi_t} & -S_{\psi_t}C_{\theta_t} & C_{\psi_t}S_{\phi_t}+S_{\psi_t}S_{\theta_t}C_{\phi_t}\\
-S_{\psi_t}C_{\phi_t}-C_{\psi_t}S_{\theta_t}S_{\phi_t} & -C_{\psi_t}C_{\theta_t} & -S_{\psi_t}S_{\phi_t}+C_{\psi_t}S_{\theta_t}C_{\phi_t}\\\
-C_{\theta_t}S_{\phi_t} & S_{\theta_t} & C_{\theta_t}C_{\phi_t}
\end{bmatrix}\\
(\mbox{ただし}, C_\theta = \cos\theta, S_\theta = \sin\theta)
例えば、加速度センサーが出力するセンサー座標系のベクトル$(a^{LCS}_x, a^{LCS}_y, a^{LCS}_z)$を上記の回転行列でグローバル座標系へと変換すると次のようになります。
R_t
\begin{bmatrix}
a_x^{LCS}\\
a_y^{LCS}\\
a_z^{LCS}\\
\end{bmatrix} =
\begin{bmatrix}
a_x^{GCS}\\
a_y^{GCS}\\
a_z^{GCS}\\
\end{bmatrix}\approx
\begin{bmatrix}
0\\
0\\
a_z^{GCS}\\
\end{bmatrix}
また、スマートフォンが完全に静止状態のときは、理論上
R_t
\begin{bmatrix}
a_x^{LCS}\\
a_y^{LCS}\\
a_z^{LCS}\\
\end{bmatrix} =
\begin{bmatrix}
0\\
0\\
g\\
\end{bmatrix}
となります。ただし、$g$は重力加速度です。
3 軸加速度センサーはスマートフォンの各軸にかかる加速度を測定するセンサーなので、静止状態では重力加速度を、運動状態では加えて運動加速度を測定しています。しかしながら、その測定値はスマートフォンの向きや姿勢によって、3 軸に分散してしまう場合があります。PDR では、歩行者のステップイベントとステップ長を加速度を用いて計算しますが、その際には縦軸の加速度値が重要となるため LCS から GCS への変換が必要となります。式を見ると回転行列によって GCS に変換されているのがよく分かります。
オイラー角
上記では、スマートフォンの 3 軸を中心とした回転角、オイラー角を用いた回転行列と座標変換について説明しました。現在はまだオイラー角についてわかっていませんが、回転行列の式を見る限り、どうやらオイラー角さえ求めてしまえば、座標変換へと辿り着けそうです。実はこのオイラー角は、加速度センサー、磁気センサーの測定値を回転行列を用いて LCS から GCS に変換する座標変換式を変形する事によって求めることができることが知られています。
参考: https://robotacademy.net.au/masterclass/measuring-motion/
まずは、先程の加速度センサーの座標変換の式を変形してみましょう。次の式は回転行列をただ乗算の形に戻したものです。
R_{\psi, t}R_{\theta, t}R_{\phi, t}
\begin{bmatrix}
a_x^{LCS}\\
a_y^{LCS}\\
a_z^{LCS}\\
\end{bmatrix} =
\begin{bmatrix}
0\\
0\\
g\\
\end{bmatrix}
両辺に対して逆行列$R_{\psi,t}^{-1}, R_{\theta,t}^{-1}, R_{\phi,t}^{-1}$を順に左から掛けていくと、次の式のようになります。
\begin{bmatrix}
a_{x}^{LCS}\\
a_{y}^{LCS}\\
a_{z}^{LCS}
\end{bmatrix} = R_{\phi,t}^{-1}R_{\theta,t}^{-1}R_{\psi,t}^{-1}
\begin{bmatrix}
0\\
0\\
g
\end{bmatrix}
ここで、回転行列の逆行列は転置行列となる性質を使って、式を展開します。
\begin{bmatrix}
a_{x}^{LCS}\\
a_{y}^{LCS}\\
a_{z}^{LCS}
\end{bmatrix}=
\begin{bmatrix}
\cos\phi_t & 0 & -\sin\phi_t \\
0 & 1 & 0 \\
\sin\phi_t & 0 & \cos\phi_t
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & -\cos\theta_t & \sin\theta_t \\
0 & \sin\theta_t & \cos\theta_t
\end{bmatrix}
\begin{bmatrix}
\cos\psi_t & -\sin\psi_t & 0 \\
\sin\psi_t & \cos\psi_t & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
0\\
0\\
g
\end{bmatrix}\\ =
\begin{bmatrix}
-\cos\theta_t\sin\phi_tg\\
\sin\theta_tg\\
\cos\theta_t\cos\phi_tg\\
\end{bmatrix}
式を見ると、加速度センサーが出力するセンサー座標系のベクトルとオイラー角の関係を単純な式で表すことができたのがわかると思います。あとは、三角関数の式をうまく変形すれば角度が求まりそうです。次の式はロール(Roll)、ピッチ(Pitch)を求める式です。
\frac{a_{x}^{LCS}}{a_{z}^{LCS}} = \frac{-\cos\theta_t\sin\phi_tg}{\cos\theta_t\cos\phi_tg} = -\tan\phi_t\Leftrightarrow \phi_t = \tan^{-1}\left( \frac{-a_{x}^{LCS}}{a_{z}^{LCS}} \right) \\\
\frac{a_{y}^{LCS}}{\sqrt{(a_{x}^{LCS})^2 + (a_{z}^{LCS})^2}} = \frac{\sin\theta_tg}{\sqrt{(-\cos\theta_t\sin\phi_tg)^2 + (\cos\theta_t\cos\phi_tg)^2}} = \tan\theta_t \\\
\Leftrightarrow \theta_t = \tan^{-1}\left( \frac{a_{y}^{LCS}}{\sqrt{(a_{x}^{LCS})^2 + (a_{z}^{LCS})^2}} \right)\ \ \ \ \mbox{ただし、}\theta_t = \pm\frac{\pi}{2}, \phi_t = \pm\pi
また関係式では、ヨー(Yaw)角がなくなってしまっています。これは、ヨー(Yaw)角をどれだけ動かしてもセンサー座標系の z 軸方向の加速度値がグローバル座標系において変わらずに必ず重力方向に向いているためです。つまり、加速度センサーからはヨー(Yaw)角を求めることができません。
なので次はヨー(Yaw)角を求めるために、磁気センサーが出力するセンサー座標系のベクトル$(b_{x}^{LCS},b_{y}^{LCS},b_{z}^{LCS})$の座標変換式を見ていきましょう。グローバル座標系において、z軸は重力ベクトルに並行で、x軸は磁北と整列しています。この場合、グローバル座標系での磁場ベクトル$B$、伏角$I$の余弦と正弦はxz平面にあります。y 方向の成分はありません。したがって、LCS から GCS への座標変換式は次のように表すことができます。
B
\begin{bmatrix}
\cos I\\
0\\
\sin I\\
\end{bmatrix}=
R_{\psi, t}R_{\theta, t}R_{\phi, t}
\begin{bmatrix}
b_{x}^{LCS}\\
b_{y}^{LCS}\\
b_{z}^{LCS}\\
\end{bmatrix}
ここでは、ヨー(Yaw)角に注目したいので、両辺に対して逆行列$R_{\psi,t}^{-1}$を左から掛けて展開します。
R_{\psi,t}^{-1}
\begin{bmatrix}
B\cos I\\
0\\
B\sin I\\
\end{bmatrix}=
R_{\theta, t}R_{\phi, t}
\begin{bmatrix}
b_{x}^{LCS}\\
b_{y}^{LCS}\\
b_{z}^{LCS}\\
\end{bmatrix}\\
\begin{bmatrix}
B\cos I\cos\psi_t\\
B\cos I\sin\psi_t\\
B\sin I
\end{bmatrix}=
\begin{bmatrix}
b_{x}^{LCS}\cos\phi_t + b_{z}^{LCS}\sin\phi_t\\
-b_{x}^{LCS}\sin\theta_t\sin\phi_t - b_{y}^{LCS}\cos\theta_t + b_{z}^{LCS}\sin\theta_t\cos\phi_t\\
-b_{x}^{LCS}\cos\theta_t\sin\phi_t + b_{y}^{LCS}\sin\theta_t + b_{z}^{LCS}\cos\theta_t\cos\phi_t
\end{bmatrix}
ここでも、磁力センサーが出力するセンサー座標系のベクトルとオイラー角の関係を単純な式で表すことができました。したがって、加速度センサー時と同様にして、ヨー(Yaw)角を求める式は次のようになります。
\frac{B\cos I\sin\psi_t}{B\cos I\cos\psi_t} = \tan\psi_t = \frac{-b_{x}^{LCS}\sin\theta_t\sin\phi_t - b_{y}^{LCS}\cos\theta_t + b_{z}^{LCS}\sin\theta_t\cos\phi_t}{b_{x}^{LCS}\cos\phi_t + b_{z}^{LCS}\sin\phi_t}\\\
\Leftrightarrow \psi_t = \tan^{-1}\left( \frac{-b_{x}^{LCS}\sin\theta_t\sin\phi_t - b_{y}^{LCS}\cos\theta_t + b_{z}^{LCS}\sin\theta_t\cos\phi_t}{b_{x}^{LCS}\cos\phi_t + b_{z}^{LCS}\sin\phi_t} \right)\\\
\mbox{ただし、}\psi_t = \pm\pi
以上で、ロール(Roll)、ピッチ(Pitch)、ヨー(Yaw)すべてのオイラー角を求めることができました。したがって、無事に座標変換にたどり着くことができます。
Custom Hook： useAttitude
ここまで、「回転行列を用いた LCS から GCS への座標変換」と「回転行列に使われるオイラー角の求め方」について説明しました。これらの話をもとに React Native で実装すると、オイラー角計算のアルゴリズムは次のとおりです。ただし、オイラー角さえわかれば座標変換の式は単なる行列の積なのでここでは省きます。
export function useAttitude(acc, mag) {
// Constractor
const acc_inv = object_sign_inversion(acc);
// States
const [attitude, setAttitude] = useState({ pitch: 0, roll: 0, yaw: 0 });
const [initYaw, setInitYaw] = useState(0);
useEffect(() => {
if (acc.x + acc.y + acc.z) {
let pitch = Math.atan2(
acc_inv.y,
Math.sqrt(Math.pow(acc_inv.x, 2) + Math.pow(acc_inv.z, 2))
);
let roll = Math.atan2(-acc_inv.x, acc_inv.z);
setAttitude((e) => ({ ...e, pitch: pitch, roll: roll }));
}
}, [acc]);
useEffect(() => {
if (mag.x + mag.y + mag.z) {
let mx = mag.x * Math.cos(euler.roll) + mag.z * Math.sin(euler.roll),
my =
mag.x * (-Math.sin(euler.pitch) * Math.sin(euler.roll)) +
mag.y * -Math.cos(euler.pitch) +
mag.z * Math.sin(euler.pitch) * Math.cos(euler.roll);
let yaw = range(Math.atan2(my, mx) - initYaw, "2PI");
if (!initYaw) {
setInitYaw(yaw);
} else {
setAttitude((e) => ({ ...e, yaw: range(yaw, "PI") }));
}
}
}, [mag]);
return attitude;
}
// function object_sign_inversion() { ... }
そして、次のようにアプリケーション内で使用します。
import React, { useState, useEffect } from "react";
import { View, Text } from "react-native";
import { Button } from "react-native-paper";
import { Accelerometer, Magnetometer } from "expo-sensors";
import { useAttitude } from "./utils/customHooks";
import { styles } from "./utils/styles";
import { round } from "./utils/sensors_utils";
export default function App() {
// Listeners
const [acc, setAcc] = useState({ x: 0, y: 0, z: 0 });
const [mag, setMag] = useState({ x: 0, y: 0, z: 0 });
const [subscription, setSubscription] = useState(null);
// Custom Hooks
const { pitch, roll, yaw } = useAttitude(acc, mag);
// Constant declarations
const dt = 100; // [ms]
Accelerometer.setUpdateInterval(dt);
Magnetometer.setUpdateInterval(dt);
const _subscribe = () => {
const sensor = {
acc: Accelerometer.addListener((data) => {
setAcc(data);
}),
mag: Magnetometer.addListener((data) => {
setMag(data);
}),
};
setSubscription(sensor);
};
const _unsubscribe = () => {
subscription.acc.remove();
subscription.mag.remove();
setSubscription(null);
};
useEffect(() => {
_subscribe;
return () => {
Accelerometer.removeAllListeners();
Magnetometer.removeAllListeners();
_unsubscribe;
};
}, [navigation]);
const deg = (ang) => {
return round((ang * 180) / Math.PI);
};
return (
<View style={styles.container}>
<Text style={styles.title}>Attitude</Text>
<Text style={styles.text}>
pitch: {deg(pitch)} roll: {deg(roll)} yaw: {deg(yaw)}
</Text>
<Text style={styles.title}>Range: (±90°, ±180°, ±180°)</Text>
<View style={styles.buttonContainer}>
<Button
style={styles.button}
dark={true}
mode={subscription ? "contained" : "outlined"}
onPress={subscription ? _unsubscribe : _subscribe}
>
{subscription ? "On" : "Off"}
</Button>
</View>
</View>
);
}
useAttitudeフックでは、引数として加速度センサーの値と磁気センサーの値を渡していますが、object_sign_inversion関数によって加速度センサーの値のみ符号を反転させています。これは、スマートフォンに搭載されている加速度センサーが、重力ベクトルの方向の軸を負とし、その反対軸を正としているためです。また、ヨー(Yaw)角に対して初期値を引いていますが、これは北を 0 度とした絶対表現からデバイスの姿勢推定が始まった瞬間を 0 度とする相対表現へと変更する処理です。
コアプロセス
さて、事前準備である座標変換システムについての説明は終わったので、この章では SmartPDR の 4 つのコアプロセスとその実装についての説明していきます。
ステップイベントの検出
歩行者の移動距離は歩数によって表されるため、より正確な屋内測位を実現するためにはこの歩数を正確に検出する必要があります。先程少し触れましたが、ステップイベントを検出するためには、スマートフォンに対する 3 軸の加速度を示す加速度センサーを利用します。ユーザーの歩数は慣性力を読み取ることによってカウントされ、定期的に観察される一連の信号パターンがステップイベントを発火します。基本的に、加速度センサーにおいては地面を基準にした縦軸にこの信号パターンが検出されます。ただし、スマートフォンの現在の向きや姿勢によっては、垂直信号成分が３つの加速度センサー軸すべてに分散される場合があります。この問題を解決するために、上記の回転行列による LCS から GCS への座標変換を実行します。
a^{GCS}_t = R_t a^{LCS}_t
次に、加速度をフィルタリングして、地球の重力の影響を取り除きます。これは約 $9.8m/s^2$のオフセットを引き起こす低周波成分であるため、単純なハイパスフィルター(HPF)が GCS の z 軸の加速度に適用されます。
g_{z, t} = \alpha g_{z, t-1}+(1-\alpha)a_{z, t}^{GCS}\\
a^{HPF} = a_{z, t}^{GCS} - g_{z, t}
ここで、$g_{z, t}$は重力成分、$\alpha$は HPF のパラメータです。$\alpha$に使用される一般的な値は$0.9 \leq \alpha \leq 1.0$の範囲です。結果の出力$a^{HPF}$には平均がゼロの高周波成分のみが含まれます。また、ランダムノイズを低減するためにローパスフィルタ(LPF)は、移動平均フィルターによって次のように処理されます。
a_{t}^{step} = a_{t}^{LPF} = \frac{1}{W}\sum_{i=-\frac{W-1}{2}}^{\frac{W-1}{2}} a_{t+i}^{HPF}
ここで、平均フィルタリングされた出力$a_{t}^{LPF}$は、次のステップカウントの手順でステップ加速度$a_{t}^{step}$として使用されます。$W$は移動ウィンドウ(奇数)であり、移動平均で使用される要素の数です。このようにして、高周波ノイズのほとんどは除去されますが、信号はその低周波属性を保持します。次に、ステップ加速度$a_{t}^{step}$に 3 つの条件を使用するピークステップカウントアルゴリズムを適用して、ユーザーが歩行している可能性のある候補を検出します。
\begin{eqnarray}
t^{peak} &=& \left\{ t \left| a_{t}^{step} > a_{t+i}^{step}, a_{t}^{step} > a_{\tau}^{peak}, |i| \leq \frac{N}{2}, i \neq 0 \right. \right\}\\
t^{pp} &=& \left\{ t \left| \mbox{max}\left( a_{t}^{step} - a_{t-i}^{step} \right) > a_{\tau}^{pp}, \mbox{max}\left( a_{t}^{step} - a_{t+i}^{step} \right) > a_{\tau}^{pp}, 1 \leq i \leq \frac{N}{2} \right. \right\}\\
t^{slope} &=& \left\{ t \left| \frac{2}{N}\sum_{i=t-\frac{N}{2}}^{t-1}\left( a_{i+1}^{step}-a_{i}^{step} \right) > 0, \frac{2}{N}\sum_{i=t+1}^{t+\frac{N}{2}}\left( a_{i}^{step}-a_{i-1}^{step} \right) < 0 \right. \right\}
\end{eqnarray}
ここで、$N$は比較対象のサンプル総数(偶数)、$t^{peak}$はしきい値$a_{\tau}^{peak}$を超えるピーク時点、$t^{pp}$は現在のピークと前の谷と次の谷の両方(peak-to-peak)の最大差がしきい値$a_{\tau}^{pp}$よりも大きい時点、$t^{slope}$は表側に正の勾配を示し、裏側に負の勾配を示す時点をそれぞれ表しています。今回しきい値は、$a_{\tau}^{peak} = 0.5 m/s^2$、$a_{\tau}^{pp} = 1.0 m/s^2$に設定します。これらの条件をすべて満たす時点であるステップイベント時点$t^{step}$は次のように取得されます。
t^{step} = t^{peak} \cap t^{pp} \cap t^{slope}
図は 15 ステップ歩いた時の赤い円でマークされた、$t^{step}$、$t^{peak}$、$t^{pp}$、$t^{slope}$を示しています。図で確認されているように、$t^{step}$の出現回数をカウントすると歩数を計算できることが分かります。
Custom Hook: useAccStep
上記の話をもとに React Native で実装すると、ステップイベントの検出アルゴリズムは次のとおりです。ただし、$W = 3$、$N = 6$、$\alpha = 0.95$に設定してあります。
function LPFilter(val1, val2, alpha = 0.95) {
return alpha * val1 + (1 - alpha) * val2;
}
export function useAccStep(acc, mag) {
// Constractor
const acc_inv = object_sign_inversion(acc);
// States
const [gravity, setGravity] = useState({ x: 0, y: 0, z: 1 });
const [movingWindow, setMovingWindow] = useState([]);
const [accStep, setAccStep] = useState(0);
const [accEvent, setAccEvent] = useState(0);
const [accList, setAccList] = useState([]);
// Custom Hooks
const attitude = useAttitude(acc, mag);
// Constant declarations
const [W, N] = [3, 6];
// Private function: a peak step counting algorithm.
const _algorithm = () => {
let acc_peak_th = 0.5,
acc_pp_th = 1.0;
let t = N / 2;
let cond = { peak: false, pp: false, slope: false };
// the peak point of time exceeding the threshold acc_peak
if (accList[t] > acc_peak_th) {
for (let i = -N / 2; i < N / 2; i++) {
if (i === 0) continue;
if (accList[t] > accList[t + i]) {
cond.peak = true;
break;
}
}
}
// the set of time point that the largest difference
// between the current peak and both of previous and next valley
let diff = { prev: [], next: [] };
for (let i = 1; i < N / 2; i++) {
diff.prev.push(accList[t] - accList[t - i]);
diff.next.push(accList[t] - accList[t + i]);
}
if (
Math.max(...diff.prev) > acc_pp_th &&
Math.max(...diff.next) > acc_pp_th
) {
cond.pp = true;
}
// the point of time that shows increment on the frontside
// and decrement on the backside
let sum = { pos: 0, neg: 0 };
for (let i = t - N / 2; i <= t - 1; i++) {
sum.pos = accList[i + 1] - accList[i];
}
for (let i = t + 1; i < t + N / 2; i++) {
sum.neg = accList[i] - accList[i - 1];
}
if ((2 / N) * sum.pos > 0 && (2 / N) * sum.neg < 0) cond.slope = true;
return cond.peak && cond.pp && cond.slope ? accList[t] : 0;
};
useEffect(() => {
if (acc.x + acc.y + acc.z) {
let acc_gcs = toGCS(acc_inv, attitude);
setGravity((g) => ({ ...g, z: LPFilter(g.z, acc_gcs.z) }));
let acc_hpf = (acc_gcs.z - gravity.z) * 9.81;
setMovingWindow((mw) => [...mw, acc_hpf]);
if (movingWindow.length === W) {
let acc_step = movingWindow.reduce((a, b) => a + b) / W;
setAccStep(acc_step);
setAccList((al) => [...al, acc_step]);
if (accList.length === N) {
setAccEvent(_algorithm);
setAccList((al) => al.slice(1));
}
setMovingWindow((mv) => mv.slice((W - 1) / 2));
}
}
}, [acc]);
return [accStep, accEvent];
}
useAccStepフックは加速度センサーの値と磁気センサーの値を入力とし、時間$t$におけるステップ加速度$a_{t}^{step}$とステップイベント時点$t^{step}$におけるステップ加速度$a_{t^{step}}^{event}$を出力します。_algorithm関数はステップ加速度$a_{t}^{step}$に 3 つの条件を適用するピークステップカウントアルゴリズムで、これを実行すると 3 つの条件を満たす場合はその時点$t$のステップ加速度$a_{t}^{step}$を返し、それ以外は 0 を返します。またtoGCS関数は、LCS のベクトル値と時間$t$におけるスマートフォンの姿勢を入力すると、グローバル座標系での加速度ベクトルを返す関数です。
さらに、歩数をカウントするには次のようにカウンタと組み合わせてuseAccStepフックを使用します。
const [accStep, accEvent] = useAccStep(acc, mag);
const [count, setCount] = useState(0);
useEffect(() => {
if (accEvent) {
setCount((c) => c + 1);
}
}, [accStep]);
進行方向の推定
ステップが検出されたら、位置推定エラーの主な原因は進行方向の歪みなので、ステップが実行された方向を知ることは非常に重要な問題です。歩行者の進行方向を推定するにはスマートフォンに対する 3 軸の地磁気を示す磁力センサーと 3 軸の角速度を示すジャイロセンサーを利用しますが、体に取り付け固定するようなセンサとは異なり、スマートフォンの配置は常に不安定であるため、歩行者の移動の進行方向を見つけるのは実際困難です。軸の傾きは常に変化しており、スマートフォンは水平を保つことができません。この傾きによって引き起こされる誤差は、補正しないと非常に大きくなり、進行方向とは全く違う方向を見つけてしまいます。したがって、ここでも座標変換の式を用いてスマートフォンが任意の位置にある時でも常に水平を保てるように LCS を GCS に変換します。
さて、それでは磁力センサーから見ていきます。磁力センサーの出力ベクトル$m_{t}^{LCS}$を地球の磁場ベクトル$m_{t}^{GCS}$に変換し、その出力の x 軸と y 軸の成分を使用して、次の式のように歩行者の進行方向を推定します。ただし、今回は方向が知りたいので$\psi_{t} = 0$とします。
m_{t}^{GCS} = R_{t}m_{t}^{LCS} = R_{\theta, t}R_{\phi, t}m_{t}^{LCS}\\
h_{t}^{mag} = 2\tan^{-1}\left( \frac{-m_{y, t}^{GCS}}{\sqrt{(m_{x, t}^{GCS})^2 + (-m_{y, t}^{GCS})^2} + m_{x, t}^{GCS}} \right)
この式で計算された角度は、実際のコンパスの読み取り値、つまり磁北に対する方位角です。真北の値を取得するには地球の自転軸に対する地球の磁場発生器の傾きによって引き起こされる磁気偏角$h_{\Delta}^{decline}$をコンパスの読み取り値から次のように推定する必要があります。
h_{t}^{mag} = 2\tan^{-1}\left( \frac{-m_{y, t}^{GCS}}{\sqrt{(m_{x, t}^{GCS})^2 + (-m_{y, t}^{GCS})^2} + m_{x, t}^{GCS}} \right) - h_{\Delta}^{decline}
次に、ジャイロセンサーを見ていきます。ジャイロセンサーはそれぞれ x軸、y軸、z軸の回転であるピッチ(Pitch)、ロール(Roll)、ヨー(Yaw)の角速度ベクトル$\omega_{t}^{LCS}$を出力します。しかし、各軸にはドリフトオフセットと呼ばれる特有の誤差(バイアス)があり、このエラーが除去されない場合、進行方向は静止状態でも時間経過とともに歪んでいきます。次の式は i 軸のバイアス$b_{i}^{gyro}$を求める式です。
\begin{eqnarray}
\varphi_{i, t} &=& \int \omega_{i, t}\ dt,\ \ \ i \in \{ x, y, z \}\\
b_{i}^{gyro} &=& \frac{\varphi_{i, t}^{start} - \varphi_{i, t}^{end}}{M\Delta t}
\end{eqnarray}
ここではまず、i 軸が出力する角速度を時間積分する事によって時点$t$における角度$\varphi_{i, t}$を求めます。次に、スマートフォンが静止状態のときの観測開始時点の角度を$\varphi_{i, t}^{start}$、観測終了時点の角度を$\varphi_{i, t}^{end}$としたときの偏差を観測数$M$とセンサーの更新時間$dt$との積で微分することで i 軸の角速度バイアス$b_{i}^{gyro}$が求まります。また、観測開始時点を更新するタイミングは磁力センサーから求めた現在の進行方向$h_{t}^{mag}$と過去の進行方向$h_{t-1}^{mag}$の差がしきい値$\beta$以下の時です。
したがって、ジャイロセンサーのバイアスによって引き起こされるドリフトは、次の式のように補正することができます。
\hat{\omega}_{i, t} = \omega_{i, t}^{LCS} - b_{i}^{gyro}
ここで、 $\hat{\omega}$ は i 軸における補正された角速度です。この値は LCS の表現であり、GCS に変換する必要があります。GCS の z 軸上の角速度$\omega_{z, t}^{GCS}$を取得するために、ここでの変換は補正された角速度ベクトル$\hat{\omega}$を重力ベクトル$g_t$にスカラー射影することによって実行されます。
\omega_{z, t}^{GCS} = \frac{\hat{\omega}_t \cdot g_t}{|g_t|} = \frac{\hat{\omega}_{t}^{T} g_t}{|g_t|}
ここで、重力ベクトル$g_t$は次の式で取得できます。
g_t = R_{t}^{-1}
\begin{bmatrix}
0\\
0\\
g_{z, t}
\end{bmatrix} = R_{t}^{T}
\begin{bmatrix}
0\\
0\\
g_{z, t}
\end{bmatrix}
ジャイロセンサーから歩行者の進行方向は、この $\omega_{z, t}^{GCS}$の時間積分によって決定できます。スマートフォンに埋め込まれたセンサーのサンプリング間隔は離散的であるため、この積分は加算と同じとして扱います。したがって、ジャイロスコープによる歩行者の動きに対応する進行方向 $h_{t}^{gyro}$は次のように得られます。
h_{t}^{gyro} = \sum_{t} -\omega_{z, t}^{GCS}
ここで、$\omega_{z, t}^{GCS}$の負の符号はジャイロセンサーの正の測定値が軸方向の定義によって負の角度変化を表しているために発生しており、符号反転を意味しています。
さて、以上のように磁力センサーとジャイロセンサーから決定された進行方向は、感知能力やユーザの動き、磁気擾乱などのためにノイズが多分に含まれいます。これらのノイズのある値から適切な進行方向を決定することは、位置特定の精度を高めるために非常に重要です。したがって、磁力センサーとジャイロセンサーからの測定値を共に使用し、ユーザーの妥当な方位方向$h_t$を見つけるアルゴリズムを適用します。
h_t = \left\{
\begin{eqnarray}
w^{pmg}\left( w^{prev}h_{t-1}+w^{mag}h_{t}^{mag}+w^{gyro}h_{t}^{gyro} \right),\ \mbox{for}\ h_{\Delta}^{cor}\leq h_{\tau}^{cor}, h_{\Delta}^{mag}\leq h_{\tau}^{mag}\\
w^{mg}\left( w^{mag}h_{t}^{mag} + w^{gyro}h_{t}^{gyro} \right),\ \mbox{for}\ h_{\Delta}^{cor}\leq h_{\tau}^{cor}, h_{\Delta}^{mag} > h_{\tau}^{mag}\\
h_{t-1},\ \mbox{for}\ h_{\Delta}^{cor} > h_{\tau}^{cor}, h_{\Delta}^{mag}\leq h_{\tau}^{mag}\\
w^{pg}\left( w^{prev}h_{t-1}+w^{gyro}h_{t}^{gyro} \right),\
\mbox{for}\ h_{\Delta}^{cor} > h_{\tau}^{cor}, h_{\Delta}^{mag} > h_{\tau}^{mag}\\
\end{eqnarray}
\right.
ただし、
\begin{eqnarray}
w^{pmg} &=& \left( w^{prev}+w^{mag}+w^{gyro} \right)^{-1}\\
w^{mg} &=& \left( w^{mag}h_{t}^{mag}+w^{gyro}h_{t}^{gyro} \right)^{-1}\\
w^{pg} &=& \left( w^{prev} + w^{gyro} \right)^{-1}\\
h_{\Delta}^{cor} &=& \left| h_{t}^{mag} - h_{t}^{gyro} \right|\\
h_{\Delta}^{mag} &=& \left| h_{t}^{mag} - h_{t-1}^{mag} \right|
\end{eqnarray}
$w^{prev}$、$w^{mag}$、$w^{gyro}$は、以前の方位方向推定、現在の地磁気ベースの進行方向、現在のジャイロセンサーベースの進行方向の重み付けパラメータであることに注意してください。しきい値$h_{\tau}^{cor}$と$h_{\tau}^{mag}$は、それぞれ相関$h_{\Delta}^{cor}$と磁力線差の変動$h_{\Delta}^{mag}$を決定するためにしようされます。
このアルゴリズムの重要な概念は、磁力センサーの変動と磁力センサーとジャイロセンサーの相関関係に基づいて、以前の推定値、磁力センサー、ジャイロスコープの中から信頼できる方位方向を選択することです。磁力センサーとジャイロセンサーが同様の出力を保つ場合にはこれらをともに使用し、対象的に、それらが異なる値を出力する場合、以前の推定値のみを使用するか、ジャイロセンサーを使用します。これらの分類された条件によって、磁力センサーとジャイロセンサーの欠点を解決し、磁気擾乱を受けた環境でも正確な進行方向が得られます。
Custom Hook: useHeading
上記の話をもとに React Native で実装すると、進行方向の推定アルゴリズムは次のとおりです。ただし、重み付けパラメータの比率$w^{prev}:w^{mag}:w^{gyro} = 2:1:1$、しきい値$h_{\tau}^{cor} = 5^{\circ}$、$h_{\tau}^{mag} = 2^{\circ}$に設定されています。
export function useGyrAngle(gyr) {
const ref = useRef({ pitch: 0, roll: 0, yaw: 0 });
const dt = 100;
useEffect(() => {
ref.current.pitch += gyr.x * (dt / 1000);
ref.current.roll += gyr.y * (dt / 1000);
ref.current.yaw += gyr.z * (dt / 1000);
}, [gyr]);
return ref.current;
}
export function useHeading(acc, mag, gyr) {
// Constractor
const acc_inv = object_sign_inversion(acc);
// States
const [gravity, setGravity] = useState({ x: 0, y: 0, z: 9.81 });
const [gyrAngTI, setGyrAngTI] = useState([]);
const [bias, setBias] = useState({ x: 0, y: 0, z: 0 });
const [headingMag, setHeadingMag] = useState({
prev: null,
current: 0,
});
const [headingGyr, setHeadingGyr] = useState(0);
const [heading, setHeading] = useState(0);
// Custom Hooks
const gyrAng = useGyrAngle(gyr);
const attitude = useAttitude(acc, mag);
// Constant declarations
const dt = 100; // [ms]
const h_decline = (7.5 * Math.PI) / 180; // Input your magnetic declination
const beta = (0.7 * Math.PI) / 180;
useEffect(() => {
if (acc.x + acc.y + acc.z) {
let acc_gcs = toGCS(acc_inv, attitude);
setGravity((g) => ({ ...g, z: LPFilter(g.z, acc_gcs.z * 9.81) }));
}
}, [acc]);
const atan2 = (y, x) => {
return 2 * Math.atan(y / (Math.sqrt(x * x + y * y) + x));
};
// Magnetometer-based heading direction
useEffect(() => {
let { pitch, roll, yaw } = attitude;
if (mag.x + mag.y + mag.z && pitch && roll && yaw) {
let mag_gcs = toGCS(mag, { ...attitude, yaw: 0 });
let h_mag = atan2(-mag_gcs.y, mag_gcs.x) - h_decline;
h_mag = range(h_mag - Math.PI / 2, '2PI');
// Calculated Gyroscope bias
if (Math.abs(h_mag - headingMag.current) > beta) {
setGyrAngTI([]);
} else {
setGyrAngTI((ti) => [...ti, JSON.stringify(gyrAng)]);
}
let num_TI = gyrAngTI.length;
if (num_TI) {
let start = JSON.parse(gyrAngTI[0]),
end = JSON.parse(gyrAngTI.slice(-1)[0]);
setBias({
x: (end.pitch - start.pitch) / (num_TI * (dt / 1000)),
y: (end.roll - start.roll) / (num_TI * (dt / 1000)),
z: (end.yaw - start.yaw) / (num_TI * (dt / 1000)),
});
}
if (!headingMag.current) setHeadingGyr(h_mag);
setHeadingMag((h) => ({ ...h, prev: h.current, current: h_mag }));
}
}, [mag]);
// Gyroscope-based heading direction
useEffect(() => {
if (gyr.x + gyr.y + gyr.z) {
let gt = toGCS(gravity, attitude, true);
let corrGyr = {
x: gyr.x - bias.x,
y: gyr.y - bias.y,
z: gyr.z - bias.z,
};
let gyr_gcs =
(corrGyr.x * gt.x + corrGyr.y * gt.y + corrGyr.z * gt.z) /
Math.sqrt(Math.pow(gt.x, 2) + Math.pow(gt.y, 2) + Math.pow(gt.z, 2));
if (headingGyr) {
setHeadingGyr((h) => range(h - gyr_gcs * (dt / 1000), '2PI'));
}
}
}, [gyr]);
// Updating heading state
// Private function: the reasonable heading direction of a user finding algorithm.
const _algorithm = (h_mag, h_gyr, h_mag_prev, h_t_prev) => {
let weight = { prev: 2, mag: 1, gyr: 2, pmg: 1 / 5, mg: 1 / 3, pg: 1 / 4 };
let threshold = {
h_cor_t: (5 * Math.PI) / 180,
h_mag_t: (2 * Math.PI) / 180,
};
let diff = {
h_cor_diff: Math.abs(h_mag - h_gyr),
h_mag_diff: Math.abs(h_mag - h_mag_prev),
};
let h_t = 0;
if (diff.h_cor_diff <= threshold.h_cor_t) {
if (diff.h_mag_diff <= threshold.h_mag_t) {
h_t =
weight.pmg *
(weight.prev * h_t_prev + weight.mag * h_mag + weight.gyr * h_gyr);
} else {
h_t = weight.mg * (weight.mag * h_mag + weight.gyr * h_gyr);
}
} else {
if (diff.h_mag_diff <= threshold.h_mag_t) {
h_t = h_t_prev;
} else {
h_t = weight.pg * (weight.prev * h_t_prev + weight.gyr * h_gyr);
}
}
return h_t;
};
useEffect(() => {
if (headingMag.current && headingGyr) {
if (headingGyr % (Math.PI / 2) <= (5 * Math.PI) / 180) {
setHeadingMag({ prev: null, current: 0 });
setHeadingGyr(0);
}
setHeading((h_prev) =>
_algorithm(headingMag.current, headingGyr, headingMag.prev, h_prev)
);
}
}, [headingMag, headingGyr]);
return heading;
}
useHeadingフックは加速度センサーの値と磁気センサーの値、ジャイロセンサーの値を入力とし、時間$t$における歩行者の進行方向$h_{t}$を出力します。_algorithm関数は磁力センサーとジャイロセンサーからの測定値を共に使用し、ユーザーの妥当な方位方向$h_t$を見つけるアルゴリズムで、これを実行すると4つの条件分岐によって、適切な方位方向が選択されます。また、useGyrAngleフックは、時間$t$におけるバイアスを求めるために使用されるジャイロセンサーの角速度の時間積分によるi軸の角度を出力します。
ステップ長の推定
総移動距離は、すべての有効なステップイベントのステップ帳を推定することで計算できます。一般に、ステップ長を推定するには静的モデルと動的モデルの2つのアプローチがあります。静的モデルは、有効なステップが同じ長さであることを前提としており、静的モデルの$k$番目のステップ長$l_k$は、次の式で決定できます。
l_k = l,\ \forall k
ここで、定数$l$は、システムを使用するユーザーによって異なります。逆に動的モデルでは、同じ人間でもステップごとにステップ長が異なるため、有効なステップの長さが異なると想定されます。したがって、特定のアプローチを使用してステップ長を推定する必要があります。歩行活動による垂直方向への衝撃は、歩幅に比例すると想定するとステップイベント間隔$a_{pp, t}^{step}$におけるステップ加速度の現在のピークと前の谷の差である垂直方向の影響は次の式で得られます。
\begin{eqnarray}
a_{pp, t}^{step} &=& a_{peak, t}^{step} - a_{valley, t}^{step}\\
a_{peak, t}^{step} &=& \left. a_{t}^{step} \right|_{t=t_{k}^{step}}\\
a_{valley, t}^{step} &=& \left. a_{t}^{step} \right|_{t=t_{k}^{head}}
\end{eqnarray}
ここで、k番目のステップイベントの尤度方位方向時間$t_{k}^{head}$は次の通りです。
t_{k}^{head} = \left. \arg\min a_{t}^{step} \right|_{t_{k-1}^{step} < t < t_{k}^{step}}
これは、進行方向は通常2つの連続するステップ間で決定されるという事実に焦点を当て、検出された各ステップイベントと推定された進行方向を表す時点を示しています。次に、$k$番目のステップ長$l_k$は、次の式のように垂直方向の衝撃によって計算されます。
l_k = \gamma\sqrt[4]{a_{pp, t}^{step}}+\delta
ここで、$\gamma$はスケールファクター、$\delta$はオフセットです。ちなみに、主4乗根の代わりに対数を使用することを検討します。
l_k = \gamma\log{(a_{pp}^{step})}+\delta
これらの2つの式結果はほぼ同じですが、参照ステップ長が大きくなるにつれて、対数ベースのステップ長の推定は、主4乗根ベースの推定よりも少しだけ正確です。このため、2つの方程式を次のように組み合わせます。
l_k = \left\{
\begin{align}
\begin{aligned}
\gamma\sqrt[4]{a_{pp, t}^{step}}+\delta,\ \mbox{for}\ a_{pp}^{step} < a_{\tau}^{step}\\
\gamma\log{(a_{pp}^{step})}+\delta, \ \mbox{for}\ a_{pp}^{step} \geq a_{\tau}^{step}\\
\end{aligned}
\end{align}
\right.
Custom Hook: useStepLength
上記の話をもとに React Native で実装すると、ステップ長の推定アルゴリズムは次のとおりです。ただし、$a_{\tau}^{step} = 3.230 m/s^2$、主4乗根の場合$\gamma = 1.479$、$\delta = -1.259$、対数の場合$\gamma = 1.131$、$\delta = 0.159$に設定されています。
export function useStepLength(acc, mag, gyr) {
// Custom Hooks
const [accStep, accEvent] = useAccStep(acc, mag);
const heading = useHeading(acc, mag, gyr);
// States
const [accList, setAccList] = useState([]);
const [headingList, setHeadingList] = useState([]);
const [valleyList, setValleyList] = useState([]);
const [accIdx, setAccIdx] = useState(-1);
const [headingIdx, setHeadingIdx] = useState(-1);
const [ret, setRet] = useState({ stepLength: 0, headingStep: 0 });
// Constant declarations
const acc_th = 3.23;
useEffect(() => {
setAccList((al) => [...al, accStep]);
setHeadingList((hl) => [...hl, heading]);
if (accEvent) {
let peakIdx = accList.indexOf(accEvent);
setAccIdx(peakIdx);
if (valleyList.length) {
let valleyIdx = argmin(valleyList, accList);
setHeadingIdx(valleyIdx);
}
setValleyList([]);
} else {
setValleyList((vl) => [...vl, accStep]);
}
let acc_peak = accList[accIdx],
acc_valley = accList[headingIdx],
acc_pp = acc_peak - acc_valley;
let fourth_root = 1.479 * Math.pow(acc_pp, 1 / 4) + -1.259,
logarithm = 1.131 * Math.log(acc_pp) + 0.159;
setRet({
stepLength: acc_pp < acc_th ? fourth_root : logarithm,
headingStep: headingList[headingIdx],
});
}, [accStep]);
return [ret.stepLength, ret.headingStep];
}
useStepLengthフックは加速度センサーの値と磁気センサーの値、ジャイロセンサーの値を入力とし、動的モデルの$k$番目の対数ベースと主4乗根ベースの２つの式を組み合わせたステップ長$l_k$と尤度方位方向時間$t_{k}^{head}$の時の進行方向$h_k$を出力します。
位置の推定
歩行者の動きは、2次元平面上の屋内の場所として表されます。移動は歩行距離と進行方向で構成されます。したがって、$k$番目のステップ$s_{k}^{user}$での現在のユーザー位置は、$k$番目のステップイベント時間$t_{k}^{step}$で、推定された進行方向$h_{k}$の前の位置$s_{k-1}^{user}$に推定された現在のステップ長$l_k$を加算することによって計算されます。
s_{k}^{user} =
\begin{bmatrix}
x_{k}^{GCS}\\
y_{k}^{GCS}
\end{bmatrix} =
\begin{bmatrix}
x_{k-1}^{GCS}\\
y_{k-1}^{GCS}
\end{bmatrix}+l_k
\begin{bmatrix}
\sin(h_k)\\
\cos(h_k)
\end{bmatrix}
ここで、$x_{k}^{GCS}$と$y_{k}^{GCS}$は、それぞれ$k$番目のステップでのGCSのx軸(東)とy軸(北)の変位を表します。
PDR 法の限界
PDR法では、スマートフォンが体の正面にある場合に限り、正確な位置の推定ができます。それは、進行方向の推定において、正面以外にスマートフォンがある場合、歩行者が向いている方向とは別方向を向いていることになるためです。したがって、ポケットの中にスマートフォンを入れて推定を行うと、大きなエラーを生んでしまいます。この問題を解決するためには、現在のような絶対的な方位方向を用いるのではなく、相対的な角度を用いる方法があります。しかしながら、この場合は新たに初期値をどのように設定するかという問題が浮上してくるので、PDR法は現在、他の屋内測位の手法と組み合わせて利用するのが一般的となっています。
まとめ
本記事では、屋内位置情報を推定するための SmartPDR について具体的に解説し、React Native を用いて実現したものをご紹介しました。初めてのQiita記事執筆で、書いてみると非常に長くなってしまい、読むのが大変になってしまいましたが、得られた知見をまとめるのに大いに役に立ちました。PDR法は魅力的ですが、未だに単独で利用することはできていないので、今後、DeepLearningなどと組み合わせて行くことで進化していくのではないかと個人的に期待しています。