ハノイの塔（Scala - Collection）

1. はじめに

Scalaで少しプログラミングが書けるようになってきたので、『データ構造』と『アルゴリズム』に関して、色々見直してみています。その中で、Stack（とQueue）の説明が書いてある書籍で、『あー、そうなのか』と言う納得感のある一文があったので、ハノイの塔のコード（Scala版）を幾つかのコレクションクラスとともに紹介したいと思います。但し、Scalaらしさ（immutable）が出せてないのが、自分の力不足な点です。

なお、自分が読んだ書籍では、ハノイの塔は、『再帰アルゴリズム』と『データ構造（スタック）』の二つについて語られており、『再帰アルゴリズム』の側面（説明）が強かったので、データ構造をあまり意識していませんでした。スタックが当たり前でしょっ！て感じです。今回、他の書籍も見直していて、アルゴリズムとデータ構造を別々に理解すると学びがありました。

細かいハノイの塔の説明は省きますが、棒AからBに移動するパターンです。（AからCもある）

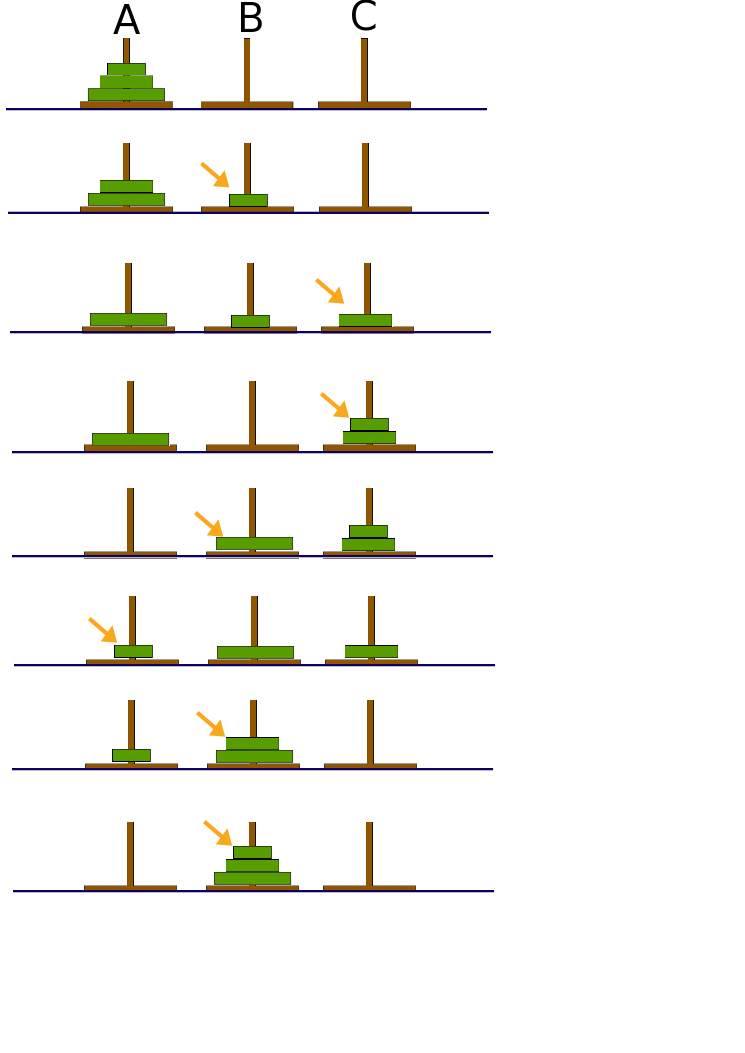
2. Array 版

クラス　MyHanoiArrayのコンストラクタ引数にArrayとしてディスクの情報を渡します。Aはディスクを積まれた状態です。B、Cは空です。Array版は moveメソッドが若干もっさりしています。

import scala.collection.mutable.Map

class MyHanoiArray(val poleA: Array[Int],
                   val poleB: Array[Int],
                   val poleC: Array[Int]) {

  // for move target position
  val rods: Map[Int, Array[Int]] = Map(1 -> poleA, 2 -> poleB, 3 -> poleC)

  // each rod disk position
  val diskPosition: Map[Int, Int] = Map(1 -> (poleA.size - 1), 2 -> -1, 3 -> -1)


  def move(n: Int, fromIndex: Int, toIndex: Int): Unit = {
    rods(toIndex)(diskPosition(toIndex) + 1) = rods(fromIndex)(diskPosition(fromIndex))  
    rods(fromIndex)(diskPosition(fromIndex)) = 0
    diskPosition.update(fromIndex, diskPosition(fromIndex) - 1)
    diskPosition.update(toIndex, diskPosition(toIndex) + 1)
    this.print()
  }

  def hanoi(n: Int, rodIndexA: Int, rodIndexB: Int, rodIndexC: Int): Unit = {
    if(n > 0){
      hanoi(n - 1, rodIndexA, rodIndexC, rodIndexB)
      move(n, rodIndexA, rodIndexB)
      hanoi(n - 1, rodIndexC, rodIndexB, rodIndexA)

    }
  }

  def run() = this.hanoi(poleA.size, 1, 2, 3)

  def print() = {
    println("----------------------------")
    println("A:" + poleA.mkString("|"))
    println("B:" + poleB.mkString("|"))
    println("C:" + poleC.mkString("|"))
  }
}

以下は呼び出し例です。BとCのディスク情報は棒Aに重ねられているディスクの枚数分の0を設定しています。

    val rodA = Array(1, 2, 3).reverse
    println("A:" + rodA.mkString("|"))
    val a = new MyHanoiArray(rodA, Array.fill(rodA.length)(0), Array.fill(rodA.length)(0))
    a.run()

以下、実行結果です。

A:3|2|1

---

A:3|2|0
B:1|0|0
C:0|0|0

---

A:3|0|0
B:1|0|0
C:2|0|0

(長いので省略)

2. Stack 版

Array版とほぼ同じですが、Stackを利用しています。使ってみるとわかるのですが、warningが出ます。StackはScala 2.11から非推奨になっています。どこかのバージョンで使用出来なく無くなっちゃいます。

MyHanoiStack.scala

import scala.collection.mutable.Stack

class MyHanoiStack(val rodA: Stack[Int],
                   val rodB: Stack[Int] = new Stack,
                   val rodC: Stack[Int] = new Stack) {

  // for move target position
  val rods: Map[Int, Stack[Int]] = Map(1 -> rodA, 2 -> rodB, 3 -> rodC)

  // disk count
  val diskCount: Int = rodA.size

  // each rod disk position
  val diskPosition: Map[Int, Int] = Map(1 -> (diskCount - 1), 2 -> -1, 3 -> -1)


  def move(n: Int, fromIndex: Int, toIndex: Int): Unit = {
    rods(toIndex).push(rods(fromIndex).pop())
    this.print()
  }

  def hanoi(n: Int, rodIndexA: Int, rodIndexB: Int, rodIndexC: Int): Unit = {
    if(n > 0){
      hanoi(n - 1, rodIndexA, rodIndexC, rodIndexB)
      move(n, rodIndexA, rodIndexB)
      hanoi(n - 1, rodIndexC, rodIndexB, rodIndexA)

    }
  }

  def run() = {
    this.print()
    this.hanoi(diskCount, 1, 2, 3)
  }

  def print() = {
    println("----------------------------")
    println("A:" + rodA.reverse.mkString("|"))
    println("B:" + rodB.reverse.mkString("|"))
    println("C:" + rodC.reverse.mkString("|"))
  }
}

以下は呼び出し例です。Arrayの時と違って、B,C は渡す必要が無いようにしてみました。

    val rodA = Stack(1, 2, 3)
    val a = new MyHanoiStack(rodA)
    a.run()

Stackクラスの説明を見てみるとこんな事が書いてあります。

(Since version 2.11.0) Stack is an inelegant and potentially poorly-performing wrapper around List. Use List instead: stack push x becomes x :: list; stack.pop is list.tail.

要は『Stackをパフォーマンスが悪いラッパーだから、リスト使ってね』です。

私が読み直していた本にも『スタックはリスト構造の操作を制限して、呼び名を与えたもの』みたいな事があって、ScalaのStackが非推奨ってなってる事に、なるほどと言う感じがしました。

3. mutable.ListBuffer 版

ListBufferを使って作って見ました。immutableでは無いのでご注意ください。

MyHanoiStack.scala

import scala.collection.mutable.ListBuffer

class MyHanoiListBuffer(val poleA: ListBuffer[Int],
                        val poleB: ListBuffer[Int] = ListBuffer.empty[Int],
                        val poleC: ListBuffer[Int] = ListBuffer.empty[Int]) {

  // for move target position
  val rods: Map[Int, ListBuffer[Int]] = Map(1 -> poleA, 2 -> poleB, 3 -> poleC)

  def move(n: Int, fromIndex: Int, toIndex: Int): Unit = {
    rods(fromIndex).head +=: rods(toIndex) 
    rods(fromIndex).remove(0)
    this.print()
  }

  def hanoi(n: Int, rodIndexA: Int, rodIndexB: Int, rodIndexC: Int): Unit = {
    if(n > 0){
      hanoi(n - 1, rodIndexA, rodIndexC, rodIndexB)
      move(n, rodIndexA, rodIndexB)
      hanoi(n - 1, rodIndexC, rodIndexB, rodIndexA)

    }
  }

  def run() = this.hanoi(poleA.size, 1, 2, 3)

  def print() = {
    println("----------------------------")
    println("A:" + poleA.reverse.mkString("|"))
    println("B:" + poleB.reverse.mkString("|"))
    println("C:" + poleC.reverse.mkString("|"))
  }
}

呼び出し方です。

    val rodA = ListBuffer(1, 2, 3)
    println("A:" + rodA.reverse.mkString("|"))
    val a = new MyHanoiListBuffer(rodA)
    a.run()

4. おわりに

javaのハノイの塔とかを見てて、色々試して見たくなったので書いて見ました。あと本当の初心者の方とか『ハノイを解くならStackじゃん！』ってなる方もいると思うので、List(Buffer)を使えるよって知ってて欲しいと思いました。（Stackは2.11から非推奨！）

ロゼッタストーン ハノイの塔(Sacal)
普通に解いてある方のコードは、『再帰（移動のみを表示）』を書いてあったりします。こう言う例が他の言語版も多いですね。あと、Prolog Solution版は私は理解できなかったです。

これからも色々勉強して少しは理解できるようになりたいです。