(zk)SNARKへの再入門

メリークリスマス！

なんか、、最初はめっちゃやる気あったけど、、結局今日のみ投稿します。内容も数式少なめ＆入門寄りです。ま、年一投稿が私のゴール。

本記事のゴールは、(zk)SNARKを聞いたことある人の(zk)SNARKの解像度を少しでもあげることです。また、本記事に関する指摘等は、コメント欄にお願いいたします。修正はしませんが、貴重な読者の皆様はコメント欄も見てくれるはずなので、きっと大丈夫です。

目次

1.(zk)SNARKとVerifiable Computation(VC)
2.SNARKの作り方
3.おまけ SNARKのTaxonomy
4.おまけ 私が抱いていた疑問
5.おまけ (zk)SNARKユースケース(Deepfake対策)

ガウス過程と機械学習っぽく言えば、1章だけでも読んでいってください。
この本、信じられないくらいわかりやすいですよね。

TL;DR

• (zk)SNARK == Honest computation
• 命題→計算f→中間表現(算術回路)→多項式表現→多項式コミットメントスキーム＆polynomial IOP＆(Fiat-Shamir変換)

(zk)SNARKへの再入門

(zk)SNARKとVerifiable Computation(VC)

私の理解では、SNARKは、効率的かつ汎用的なVerifiable Computation(VC)を実現する技術の１つです。SNARKを用いると、証明者(Prover)は検証者(Verifier)に対して、「ある計算$f(x)$の計算結果が$y$であること」を証明することができます。$y=f(x)$かどうかは、検証者が再計算すればもちろんわかりますが、検証者は再計算することなく証明者からもらった証明を検証することで$y=f(x)$であることを確信できます¹。

SNARKのSはSuccinct(簡潔な)のSで、アルゴリズムによりますが、証明者が送る証明のサイズは数百～数千bytesです²。SNARKのNはNon-interactive(非対話)のNで、証明者と検証者はやり取りする必要がなく、証明者側で証明を作成し、一方的に検証者に証明を送るだけで良いです³。ARKはARrguments of Knowledgeで、$y=f(x)$となるような$x$及びその中間出力を知っていることを証明します⁴。これで皆さん、SNARK、完全におさらい＆理解しましたね。

zkSNARKは先頭にzkとある通り、証明者は入力$x$を明かさずに計算結果$y=f(x)$を証明することができます($y=f(x)$となるような$x$を知っていることを証明します⁵)。証明者は証明したい命題を計算$f$として表現し、zkSNARKを適用することで、汎用的なゼロ知識証明を実現することができます。汎用的なゼロ知識証明と表現したのは、命題を計算$f$で表現できれば、様々な命題を証明できるからです。zkSNARKは、しばしばGeneral-purpose ZKPsと言われたりします⁶。

長くなりましたが、(zk)SNARK再入門とのことで、SNARKはVCを実現する技術だと説明しました。SNARKにゼロ知識性を付与することで、任意の計算結果$y=f(x)$を、入力$x$を教えなくても証明できます。18歳以上であることを証明したければ$f(x)=x-18 >= 0$とすれば良いし、ハッシュの原像をしっていることを証明したければ例えば$f(x)=\text{SHA256}(x)$として、SNARKを適用すれば良いわけです(本当にそれだけで十分なんだっけ？)。

ゼロ知識証明という単語を出すと、ゼロ知識という単語に引っ張られるせいか、"○○を明かさずに××"といった説明がどうしても記憶に残ると思います。(zk)SNARKのゼロ知識性も魅力的ですが、証明者は$y=f(x)$が正しいことを証明できる＆検証者は計算結果($y=f(x)$)が正しいことを高速に確認できるという点が(zk)SNARKの真の魅力だと私は勝手に考えています。

実際、この記事を書くのに大いに参考したProofsArgsAndZK(有名な先生が書いたzkSNARKに関するサーベイ論文)のIntroでは、VCという単語がまず出てきます。

ProofsArgsAndZK Chapter1より

また、zkSNARKに関する私が好きな資料の１つであるdemystifying-zero-knowledge-proofsでは、以下のようなスライドが出てきます。

demystifying-zero-knowledge-proofsより

このスライドでは、ZKPs==honest computationと表現されていますね。

これ以降では、(zk)SNARKの作り方をざっくり説明します。先ほどから(zk)SNARKと、zkに括弧を付けていますが、ゼロ知識性の実現方法は本記事では割愛します。ProofsArgsAndZKでも、ゼロ知識性に関してはChapter11以降から語られます。「いや、俺はどうやってゼロ知識性を実現しているかだけが知りたいんだ」という方のために、有識者に怒られる書き方でざっくり説明すると、乱数で多項式をマスクしたり、多項式コミットメントスキームの性質を活用することでゼロ知識性を付与します。以上です。詳細はProofsArgsAndZKのChapter13が参考になります。それでは、SNARKの作り方を見ていきましょう。

SNARKの作り方

端的に言えば、Polynomial IOPと多項式コミットメントスキーム(とFiat-Shamir変換)を組み合わせることでSNARKを作ることができます。
もう少し書くと、

• 証明したいことを算術回路(Arithmetic Circuits)で表す
• 算術回路および各ゲートの割り当てを多項式で表現し、polynomial IOPによってそれが正しいことを証明する
• 多項式コミットメントスキームを組み合わせることにより、Succinct(簡潔な)証明を作成
• Fiat-Shamir変換によってNon-interactive(非対話型)証明を得る

です。

まあ、Justin Thaler先生のわかりやすい論文やVideoをただそのまま和訳しています。

算術回路、多項式表現、Polynomial IOP

まず初めに、証明したい計算$f$を算術回路で表現します⁷。足し算ゲートと掛け算ゲートを用いて表現します⁸。例えば、以下、ZKP MOOC Lecture4のスライドp77の真ん中図のような感じです。

ZKP MOOC Lecture4のスライドp77より

$y=f(x)$であると検証者を説得するには、証明者は、算術回路の各ゲートの割り当て(Transcript、上スライドの右下図)が正しいということを証明すれば良いです(くどいですが、足し算ゲートの割り当て値はゲートへの2入力から足し算した結果であり、掛け算ゲートの割り当て値はゲートへの2入力から掛け算した結果であることを証明すれば良いです)。

以降、その割り当てをトランスクリプト$T$と表現します。$T$は$x \in \lbrace0,1\rbrace^{\log S}$から割り当てた値を返す関数です。ここで、$S$はゲート数です($S$個のゲートそれぞれにビット列のラベルを付けるには、$\log S$ビットで十分ですね)。そして、トランスクリプト$T$の定義域を拡張した多項式$h$を考えます。$h$は$T$の定義域$x \in \lbrace0,1\rbrace^{\log S}$から$x \in \mathbb{F}$に拡張された、以下を満たす多項式です⁹。
$$h(x) = T(x) \quad \forall x \in \lbrace0,1\rbrace^{\log S}$$

また、以下のような多項式$g_h(a,b,c)$を考えます。ここで、$add(a,b,c)$は、ゲート$a$が、ゲート$b$とゲート$c$の足し算であるときに1,それ以外では0を返すような関数です。$mul(a,b,c)$は、ゲート$a$が、ゲート$b$とゲート$c$の掛け算であるときに1,それ以外では0を返すような関数です。

$g_h(a,b,c) = \text{add}(a, b, c) \cdot (h(a) - (h(b) + h(c))) + \text{mult}(a, b, c) \cdot (h(a) - h(b) \cdot h(c))$

もしトランスクリプト$T$が本当に正しければ、以下の式(1)が成り立つはずです(そうなるように$add(a,b,c)$や$mul(a,b,c)$を導入したわけです。例えば、$add(a,b,c)=1$の時、$h(a) - (h(b) + h(c))=0\iff h(a)=h(b) + h(c)$となります)。

$$g_h(a, b, c) = 0 \quad \forall (a, b, c) \in \lbrace0,1\rbrace^{3 \log S} \tag{1}$$

$g_h(a,b,c)$は3変数多項式ですが、一旦、1変数多項式$g_h(x)$で表現できるとすると、$\forall (a, b, c) \in \lbrace0,1\rbrace^{3 \log S}$の代わりになるようなある集合$H \subseteq \mathbb{F}$で0になる多項式$Z_H(x)$で、$g_h(x)$を割り切れるはずです。

$$Z_H(x) := \prod_{a \in H} (x - a)$$

つまり、$g_h(x) = q(x) \cdot Z_H(x)$となるような商$q(x)$が存在します。証明者が本当に計算$f$を行い、正しいトランスクリプト$T$を知っているなら、証明者は商$q(x)$を計算できます。そして、検証者はランダムに選んだ点$r$において以下式が成り立つことを確認することで、トランスクリプト$T$が確かに正しい割り当てであることを確認できます。

$$g_h(r) = q(r) \cdot Z_H(r)$$

なぜ$r$での評価のみで良いんでしょうか？よくよく考えたら、$d$次元多項式って、０になるところは$d$点しかないですよね。$d$次元多項式の定義域(domain)が十分広い時、ランダムに選んだ点$r$で評価したら$f(r)=0$になる確率もすごく低そうですよね。さらに次のことも言えそうです。二つの$d$次元多項式$f,g$があった時、もしランダムに選んだある点$r$での評価値が一致したら($f(r)=g(r)$)、その多項式が同じ多項式である確率は高そうですね。二つの$d$次元多項式って、高々$d$点でしか交わらないからです。ランダムに選ぶ点$r$の範囲が十分広い時、評価値が一致したら、おそらくそれは同じ多項式だということです(違う多項式なのに交わる点をたまたま選んでしまう確率は$\frac{d}{\mathbb{F}}$)。より詳しくはSchwartz-Zippel Lemmaで検索してください。

Schwartz-Zippel Lemmaより、証明者が本当に正しいトランスクリプト$T$を知っているのかを確認したければ、ランダムに選んだ点$r$で、$g(r)=q(r)Z_H(r)$が成り立つかを確認すればよいということです。

トランスクリプト$T$の定義域を拡張した多項式$h$を考えたのは、上述のSchwartz-Zippel Lemmaより、ランダムに選ぶ点$r$の範囲が十分広くなければいけないからです。

いくつか対処していない問題(e.g. 一旦1変数とした)がありますが、ざっくり説明なので、省略します(ZKP MOOC Lecture4 p91を参照してください)。

多項式コミットメントスキーム

ここまでわかったこととして、どうやらある多項式に関してある点での評価値がわかれば、検証者は、証明者が$y=f(x)$となるような$x$を知っていると信じてよさそうです。では、それはどのように実現できるでしょうか？Trivialなやり方は、多項式そのものを検証者に送り計算してもらえばよいですね。しかしこのやり方は、Succinctではありません¹⁰。また、本記事のスコープ外ですが、多項式そのものを送ってしまうとゼロ知識性も実現できなそうです。

SNARKのSを実現するには、多項式コミットメントスキームと呼ばれる道具を用います。多項式コミットメントスキームでは、証明者は多項式からコミットメント$commit(f)$を作成し検証者に送ります。その後、検証者は乱数$u$での評価値$v=f(u)$を、証明者から送られた証明から高速に確認することができます。以下、ZK MOOC lecture6からの引用です。

https://zk-learning.org/assets/lecture6.pdf p5より

多項式コミットメントスキームとして、様々な手法が提案されています。KZGコミットメントスキームなど、有名なのは解説記事があります。みんな大好きMerkle Treeも(多項式)コミットメントスキームとして用いることができます(実際はlow-degree testsなるものと組み合わせる必要があるので、括弧をつけます¹¹)。ざっくり述べると、多項式$f$の各評価値をMerkle Treeの葉として、ルートハッシュをコミットメントとして送ります。点$u$での評価値$y=f(u)$を証明したければ、葉$f(u)$からルートハッシュまでのパスに必要なノードを検証者に送信すればよいです。

ProofsArgsAndZKのTable16.1では、様々な(Trusted Setupのいらない)コミットメントスキームの特徴がまとめられています。

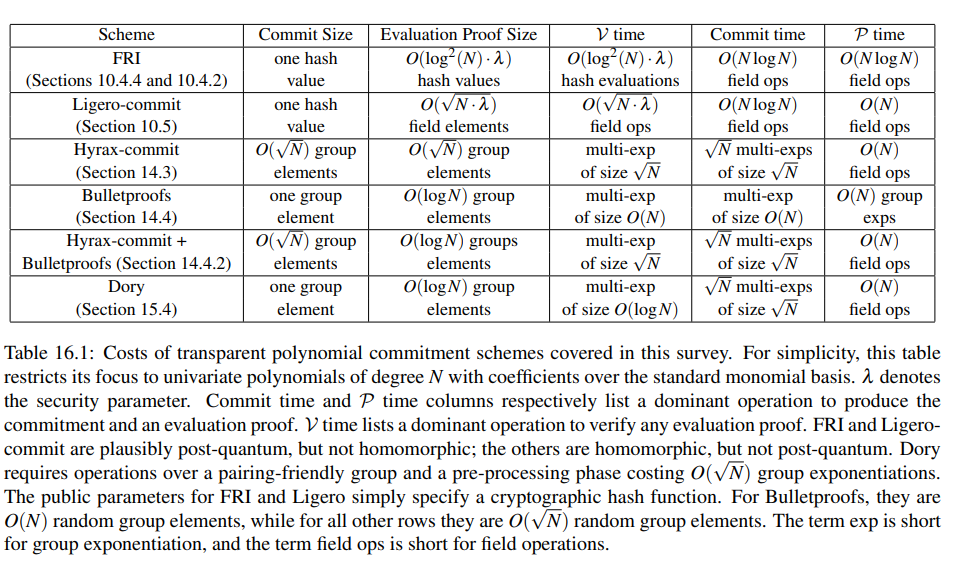
ProofsArgsAndZKのTable16.1より

Fiat-Shamir変換

最後に、SNARKのN(Non-interactive)を実現しましょう。Fiat-Shamir変換を用います。Fiat-Shamir変換は、シュノア署名とかで出てきますね(wiki、ref)。

Fiat-Shamir変換を用いることにより、多項式コミットメントスキームにおける検証者が送る乱数$u$を、証明者側で作ることができます。具体的には、証明者と検証者のそれまでのやり取りと、SHA3等のハッシュ関数を用いることで計算します。以下、ProofsArgsAndZKのFigure 5.1が非常にわかりやすいです。Random Oracleはハッシュ関数に読み替えてください。

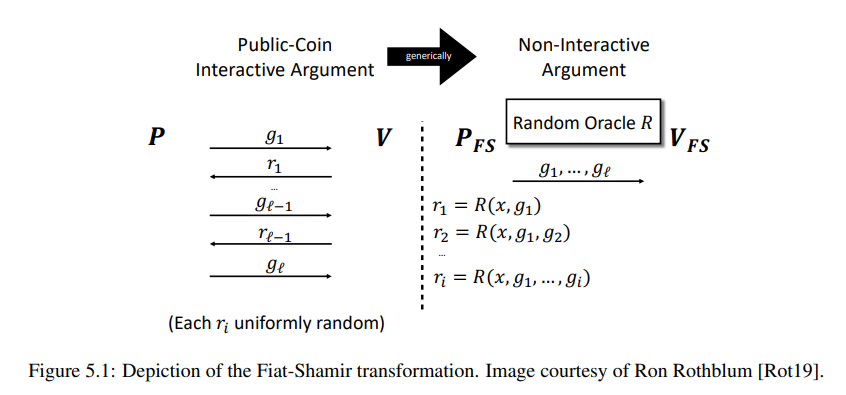
ProofsArgsAndZK Figure5.1より

ポイントは、ハッシュ関数に何を入力すべきか、という点です。入力に漏れがあると、脆弱性がうまれます。Fiat-Shamir変換のセキュリティに関しては日本語の記事もあり、脆弱性をうむポイントになるようです(ZKP MOOC Lecture8 p66以降も参考になります)。

Fiat-Shamir変換のイメージとしては、攻撃者が相手を騙す材料を作るためにあらかじめ知っときたい値$u$を、相手を騙す材料から作ってもらうスキームにすれば、ハッシュ関数をめちゃくちゃ実行できなければ、騙すことができないという感じでしょうか¹²。

多項式コミットメントスキームにおけるハッシュ関数への入力は、例えば、EIP4844のこれとか見ると良いんですかね。

例えば、go-kzgというリポジトリのコードには、多項式とそのコミットメントが入力されている？ようです。

Fiat-Shamir変換により検証者から乱数$u$を送る過程を除くことで、SNARKが完成しました。ざっくりですが、以上です。個々の細かい所は、私も今後勉強していきたいですし、記事をきっと、いやおそらく書いていきます。

まとめ

読んでくださりありがとうございました。25日になってしまったので、不完全ですが投稿します。本当は10記事くらい出すとか決めてアドカレ作ったはいいけど、、まあ、そんなもんですね。(zk)SNARK、関心が高まってくと良いですね。自分が受け取ったメールを証明するとか、面白いですよね。zkMLとかも、掘りたいですね。あ、いいねください。

参考

[1] https://people.cs.georgetown.edu/jthaler/ProofsArgsAndZK.pdf
[2] https://zk-learning.org/assets/lecture4.pdf
[3] https://people.cs.georgetown.edu/jthaler/ProofsArgsAndZK.html

[1]では、以下全部詳しく学べるので、めちゃ良いです。

• Polynomial IOP (IP, MIPs, PCPs, IOPs)
• いろんな多項式コミットメントスキーム
• Fiat-Shamir変換
• Sum-check protocol
• GKR protocol
• multi-linear polynomial extension
• Schwartz-Zippel Lemma
• Circuit Satisfiablity, R1CS-Satisfiability

[2]でも、これらをさっと学べます。動画派の方にもおすすめです。

[3]のSupplementary Video ResourcesからJustin先生の動画が見れます。3つとも非常に参考になります。

おまけ SNARKのtaxonomy

SNARKはPolynomial IOPと多項式コミットメントスキームで作るといいましたが、それらの具体的なアプローチによってSNARKを分類できるようです。

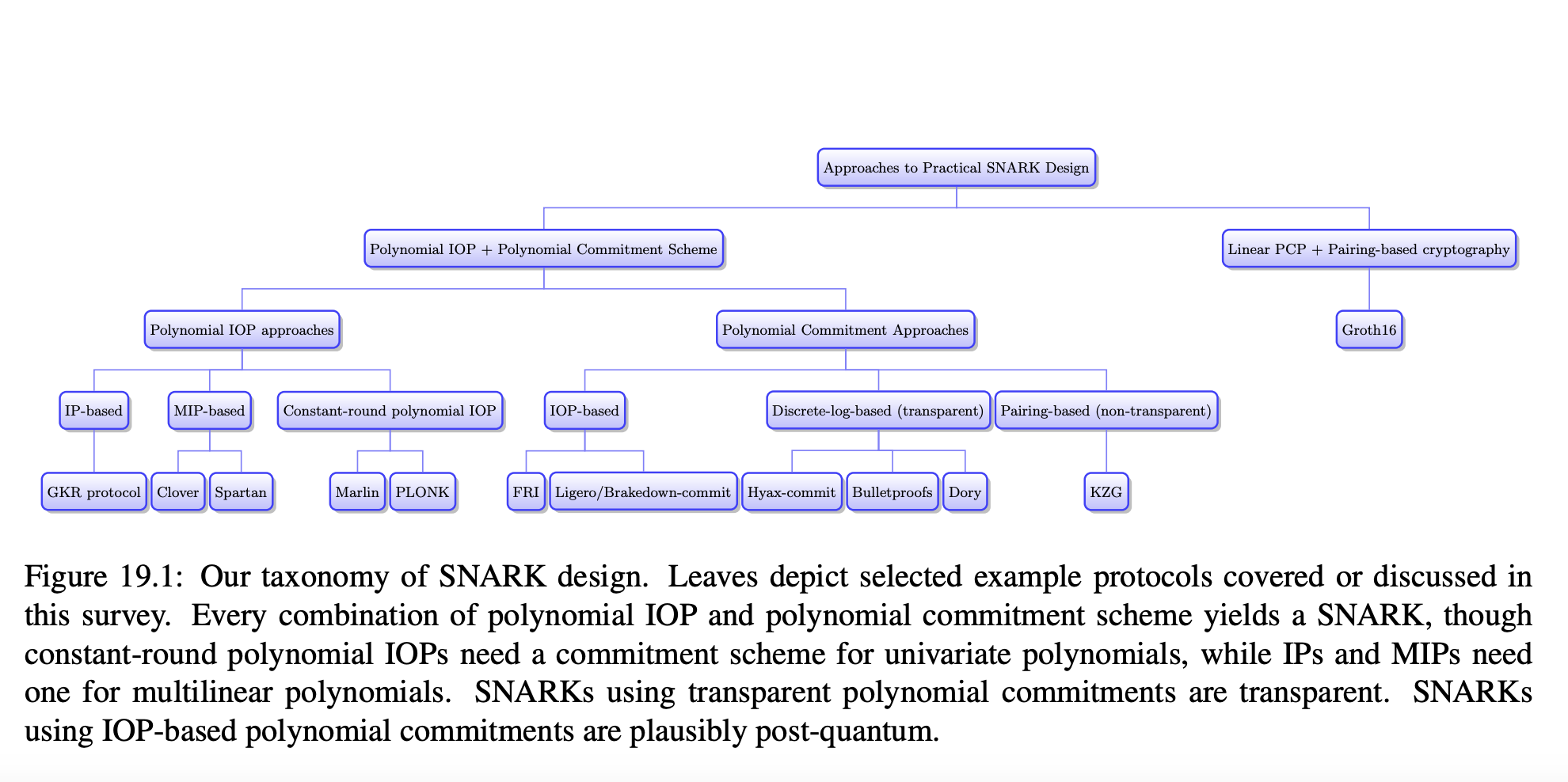
ProofsArgsAndZKのFIgure 19.1より

zkSNARKの有名な手法として、Groth16がありますが、この手法は図の通り、言ってしまえば亜種です。Groth16は、この図が示すように、Linear PCPに基づいた手法です。Linear PCPに基づいた手法に興味がある方は、以下のわかりやすい記事や、ProofsArgsAndZKのChapter17を参照してください。
https://zenn.dev/qope/articles/f94b37ff2d9541

ProofsArgsAndZKの19.2 Pros and Cons of the Approachesに、それぞれの特徴がまとまっています。すべてまとめませんが、例えば、Trusted Setupが必要かどうかや、耐量子性があるかどうかは、用いる多項式コミットメントスキームに左右されます。

おまけ 私が抱いていた疑問

例えば、18歳以上であるという年齢証明をSNARKで実現したいときに、年齢$x - 18 >= 0$となる$x$を知っていることだけ証明しても、なんも意味なくね？と思っていました。こういったユースケースを社会実装する際には、誰かに年齢等に署名してもらい、署名検証も計算$f$に含める必要があるという理解です。つまり、証明者が実行および証明すべき計算$f$は、
「あなたが信頼している公開鍵で署名検証を行い、その署名の対象メッセージ(年齢)から18引いた値の正負結果および署名検証結果」となります。(そのクレデンシャルの持ち主である証明なども本当は必要です)。

ゼロ知識証明がもともと、クラスNPの問題の答えを知っていることのみを証明したいという話から出てきている?のを考えれば、色々納得できます。Witness(証拠)という単語も、計算理論のお話から出てきているのだろうという理解です。ProofsArgsAndZKにも、ここらへんのお話はちょこちょこ出てきます。

おまけ (zk)SNARKユースケース

Deepfake等の対策として、カメラで写真撮影した瞬間に、カメラ内のチップで署名付与するというやり方があります（参考）。

Dan Boneh先生の資料及び記事にも出てきます。

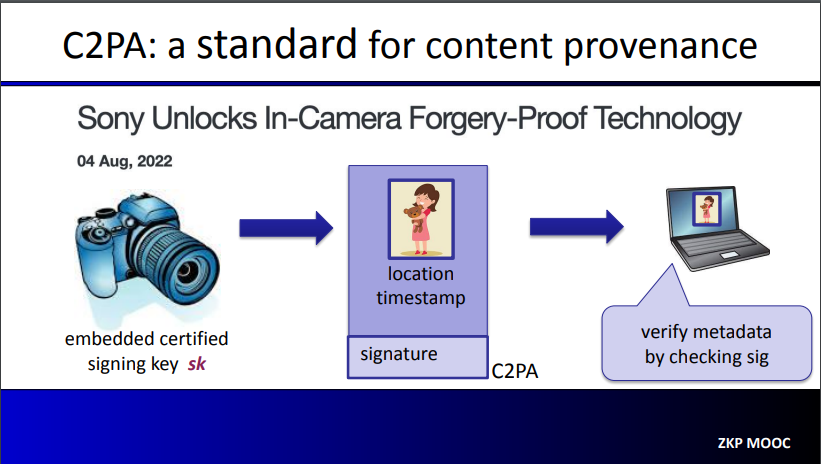
https://zk-learning.org/assets/Lecture2-2023.pdf p11より

しかし、撮った写真を編集すると、元の署名が有効ではなくなってしまうという課題があります。この課題は、計算$f$を「元の画像の署名検証および編集後画像が元画像に対する編集処理結果であることの確認」として、(zk)SNARKを適用することで解決できます。また、ゼロ知識性は、モザイクをかけたいなどの要求にも有効です。

これをHalo2で実装する論文も出てきています。しかし、実装が公開されていないため、切り抜き編集のみを対象として自分で実装した結果、大体論文の結果と一致しました。

1. 部下に頼んだ仕事$f$を、きちんと行ったかどうかを仕事$f$を再実行することなく確認できるわけです ↩

2. 一般的には、多項式コミットメントスキームによって実現されます。 ↩

3. 一般的には、Fiat-Shamir変換によって実現されます。 ↩

4. Proof (of Knowlegdge)と違いArgument (of Knowledge)は、多項式時間(Polynomial Time)の不正な証明者に対してのみ健全性が保証されます ↩

5. 明かしたくないこと($w$)と、明かしてもよいこと($x$)を分けて$f(x,w)$と表現したりしますが、本記事では$f(x)$と一括りで表します。$w$はwitness(証拠)の$w$です ↩

6. 例えばこの論文のタイトルやアブストに書いてあります。GPGPUみたいな感じかな、知らんけど。証明したいことをとにかく計算$f$に落とし込むわけですね。 ↩

7. (zk)SNARKの多くの実装は、front-endとback-endに分けられます。計算$f$(プログラム)を回路に変換する部分をfront-endと呼びます。変換された回路に対する証明システムをback-endと呼びます(参考1:ProofsArgsAndZK Chapter6 6.1 Introduction、参考2:ZKP MOOC Lecture2 p61) ↩

8. 秘密計算同様、足し算と掛け算を考えれば十分、だよね？見せ算も、足し算と掛け算で表現できることが知られています(link) ↩

9. 任意の$T : \lbrace0,1\rbrace^l \to \mathbb{F}$は、$\mathbb{F}$上での一意な多項式で表現できるそうです(ProofsArgsAndZK p29 Fact3.5) ↩

10. いや、Succinctってなんだよって感じですが、ProofsArgsAndZK 7.2では、トータルの通信量がWitness $w$に対してsublinearであるとしています。いや、sublinearってなんだよって感じですが、ProofsArgsAndZK p109脚注では、$o(|w|)$とされています。 ↩

11. もっと言えば、それでも多項式コミットメントスキームとはならないようです。(ProofsArgsAndZK p111) ↩

12. 自分の希望年収を教えてから相手に年収を教えてもらう仕組みだと、相手はいくらでも嘘がつけてしまいますが、相手の年収から自分の希望年収が算出されるようにすれば良い感じでしょうか(全然違う)。 ↩