メモ

• 概要
  • 縮約：
  • 主成分分析：
  • 部分空間法：
  • カーネル主成分分析、カーネル部分空間法：

---

• 概要
  • 縮約：データの次元空間をより次元の低い次元空間にすること
  • 主成分分析：縮約の手法の１つ、共分散行列の固有値問題をとき、大きな固有値を持つ固有ベクトルで部分空間を構成し元の情報を表現する

---

• 概要
  • 部分空間法：クラスごと主成分分析を行いそれぞれの部分空間を構成してパターン認識を行う方法
  • カーネル主成分分析、カーネル部分空間法：カーネル法を使った主成分分析、部分空間法

---

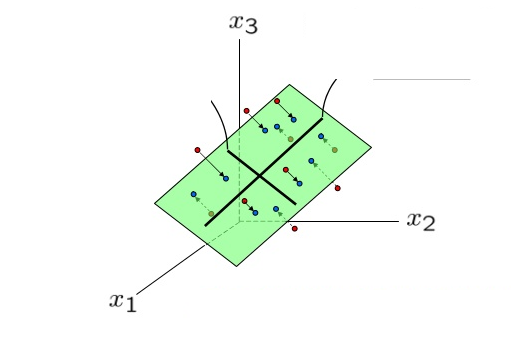
• 縮約のイメージ

---

• 部分空間
  • 部分空間の定義
    • d次元ベクトル空間Vの部分空間
    • Vのベクトル　$x_1$ ,・・・・・$x_r$ (r<=d)
    • W={$a_1x_1 +・・・+a_rx_r $}
      • $x_1$ ,・・・$x_r$ の１次結合の集合
    • Wがr次元の部分空間であるためには$x_1$ ,・・・$x_r$が１次独立でないといけない
  • １次独立：どの$x_1$もほかの$x_j$の線形結合で表現できないこと

---

• 正規直交基底（１次独立なベクトル）を見つける方法
  • グラムーシュミットの正規直交化:代数的手法
    • QR分解：行列を使って解く方法
  • 主成分分析：
    • 特異値分解：

---

-グラムーシュミットの正規直交化

(1) \vec{n_1} = \vec{x_1} / ||\vec{x_1}|| :正規化\\
(2) \vec{\tilde{n_i}} = \vec{x_j} - \sum_{j=1}^{i-1}(\vec{n_j}^T\vec{x_i})\vec{n_j},\\
\vec{n_i} = \vec{\tilde{n_i}} / ||\vec{\tilde{n_i}}|| \\

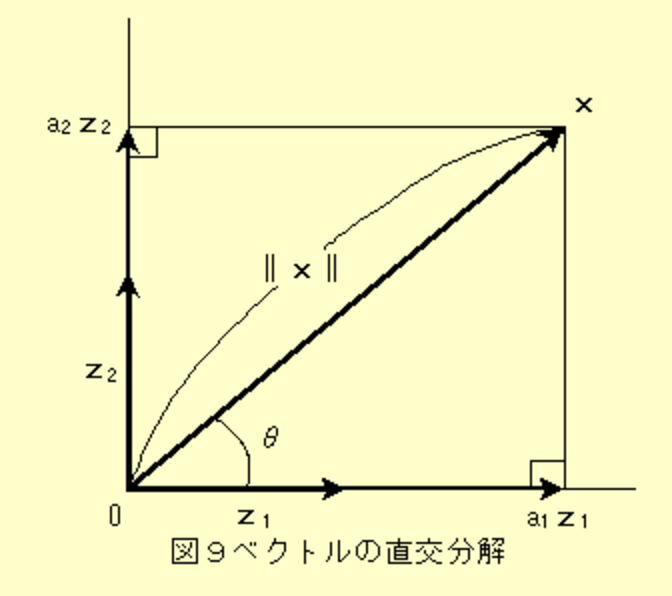
\vec{n_1}^T\vec{x_2} := \vec{x_2}のn1方向の長さ\\
(\vec{n_1}^T\vec{x_2})\vec{n_1} := \vec{x_2}のn1方向の成分\\
\vec{\tilde{n_2}} = \vec{x_2} - (\vec{n_1}^T\vec{x_2})\vec{n_1}\\
\vec{n_2} = \vec{\tilde{n_2}} / ||\vec{\tilde{n_2}}|| 

---

• 主成分分析
  • 分散が最大になる方向への線形変換を求める手法
    • 共分散行列をつかって固有値問題を解く
  • 第１主成分：最大固有値に対応する固有ベクトルで線形変換された特徴量
  • 全分散量：固有値の総和
  • 寄与率：固有値／全分散量

---

学習データ$X=(x_i1,...x_id)^{\mathrm{T}}(i = 1,...,N)$の分散が最大になる方向への線形変換を求める手法。

共分散行列
\sum = Var\{\bar{X}\} = \frac{1}{N}\bar{X}^{\mathrm{T}}\bar{X}\

$\bar{X}=(x_1 - \bar{x}....,x_N - \bar{x})^{\mathrm{T}}$：平均ベクトルを引き算したデータ行列

線形変換 with 係数ベクトルa_j

s_j = (s_{1j},....s_{Nj})^{\mathrm{T}} = \bar{Xa}_j

$s_{1j},....s_{Nj}$の平均が0となる

Var\{{s_j}\} = \frac{1}{N}{s}_j^Ts_j = \frac{1}{N}(\bar{Xa}_j)^{\mathrm{T}}(\bar{Xa}_j) = \frac{1}{N}{a}_j^T\bar{X}^{\mathrm{T}}\bar{Xa}_j = a_j^TVar\{{\bar{X}\}}a_j \

係数ベクトル$a_j$のノルムを1に制約したラグランジェ関数を解く

E(a_j) = a_j^TVar\{{\bar{X}\}}a_j - \lambda(a_j^T - 1)

が最大にする$a_j$を見つける。
$\lambda$はラグランジェ未定定数
$a_j$で微分し＝０

\frac{\partial E(a_j)}{\partial a_j} = 2Var\{{\bar{X}\}}a_j - 2\lambda a_j = 0 

より

Var\{\bar{X}\}a_j=\lambda a_j

得られる固有値を$\lambda_1\geq...\geq\lambda_d$、
対応する固有ベクトルを$a_1,...,a_d$とする

最大固有値に対応する固有ベクトルで線形変換した特徴の分散は、

Var\{{s_1}\} = a^T_1Var\{\bar{X}\}a_1 = \lambda _1a^T_1a_1 = \lambda _1

最大固有値に対応する固有ベクトルで、線形変換された特徴量を第1主成分という。
変換された特徴量の分散は固有値に一致するので、全分散量＝各主成分の総和

V_{total} = \sum_{i=1}^d \lambda _i

$k$成分の寄与率

c_k = \frac{\lambda _k}{V_{total}}

第$k$成分までの累積寄与率$\gamma _k$は

\gamma _k = \frac{\sum_{i=1}^k \lambda _i}{V_{total}}

---

• 特異値分解：SVD
  • SVD：QR分解とは異なる分解手法

主成分分析に関連した行列の分解法：特異値分解(SVD)

特徴値分解　$X = U \Lambda V^{\mathrm{T}}$
任意の$n \times p$行列$X$

= (u_1 u_2 ... u_p) 
  \left(
    \begin{array}{cccc}
      \sqrt{λ_1} & 0 & \ldots & 0 \\
      0 & \sqrt{λ_2} & \ldots & 0 \\
      \vdots & \vdots & \ddots & \vdots \\
      0 & 0 & \ldots & \sqrt{λ_p}
    \end{array}
  \right)

  \left(
    \begin{array}{cccc}
      \upsilon^T_1 \\
      \upsilon^T_2 \\
      \vdots \\
      \upsilon^T_p 
    \end{array}
  \right)

$U$は$XX^{\mathrm{T}}$の非ゼロ固有値に対応する固有ベクトルからなる、$n \times p$列正規直交行列である。
$V$は、$X^{\mathrm{T}}X$の非ゼロ固有値に対応する固有ベクトルからなる、$p \times p$列正規直交行列である。
$\Lambda$は、$XX^{\mathrm{T}}$または$X^{\mathrm{T}}X$の非ゼロ固有値の平方根（特異値という）$p \times p$対角行列である。

特異値分解と主成分分析の関連

$n \times p$行列$X$を$p$個の属性をもつ$n$個のデータ（あらかじめ平均ベクトルが引かれているものとする）と考えると　$X^{\mathrm{T}}X$は共分散行列
その固有値と固有のベクトルが$\lambda _i$と $\upsilon _i$とみなせる

$X= U \Lambda V^{\mathrm{T}}$より$XV = U \Lambda$より

(X\upsilon _1 \ \ X\upsilon _2 \ \ ... \ \ X\upsilon _p) = (\sqrt{\lambda _1 u_1} \ \ \sqrt{\lambda _2 u_2} \ \ ... \ \ \sqrt{\lambda _p u_p})

分散は、

Var\{{X_\upsilon{_1}}\} = (X_\upsilon{_1})^{\mathrm{T}}(X_\upsilon{_1}) = \left( \sqrt{\lambda _1 u_1} \right)^{\mathrm{T}}\left( \sqrt{\lambda _1 u_1} \right) = \lambda_1

第1主成分から第$q(\leq p)$主成分までの$\upsilon_i$で構成された部分空間は

\tilde{V} = (\upsilon_1 \ \ ... \upsilon_q)

$\tilde{V}$へのデータ$X$の射影は$X\tilde{V}$は、共分散行列が

Var{\{X\tilde{V}\}} =   \tilde{V}^{\mathrm{T}}V\Lambda^{\mathrm{2}}V^{\mathrm{T}}\tilde{V}

$\tilde{V}^{\mathrm{T}}V$は、

\tilde{V}^{\mathrm{T}}V =   \left(
    \begin{array}{cccc}
      \upsilon^T_1 \\
      \vdots \\
      \upsilon^T_q 
    \end{array}
  \right) \ \ 
(\upsilon_1 \ \ ... \upsilon_q) =   \left(
    \begin{array}{cccc}
      1 & 0 & \ldots & 0 & 0 & \ldots & 0 \\
      0 & 1 & \ldots & 0 & 0 & \ldots & 0 \\
      \vdots & \ddots & \ddots & 0 & \vdots & \vdots & \vdots \\
      0 & \ldots & 0 & 1 & 0 & \ldots & 0
    \end{array}
  \right)

となるので、共分散行列は、

Var\{X\tilde{V}\} = \lambda^2_q

となる。$\Lambda_q$は、特異値分解の最初の$q$個の特異値以外を0とした対角行列である。$\Lambda$の代わりに$\Lambda_q$を用いた行列の分解

\tilde{X} = U\Lambda_qV^{\mathrm{T}} = \sum_{i=1}^q \sqrt{\lambda _i u_i u^T_i}

は、$X$のランク$q$の誤差最小という意味での最良近似となっている。

---

• 部分空間法
  • ：他クラスの識別器を構成できる
  • ２つの手法：相関行列を使うCLAFIC法、共分散行列を使う方法
    • 違いは平均ベクトルを引いて、平均ベクトルを中心としたデータばらつきをみる共分散行列を使う方法は部分空間の原点はそれぞれの平均ベクトル、相関行列を使う方法は原点が共通でデータのばらつき自体を比較
  • CLAFIC法
  • 射影行列：射影行列は部分空間と等価である
  • 残差ベクトル
  • その他：混合類似度法、差分部分空間法、相互部分空間法

---

• カーネル主成分分析
  • カーネルによって，データ数×次元数の行列をデータ数×データ数の行列に変換したのちに主成分分析を行う
• カーネル部分空間法
  • カーネルによって，データ数×次元数の行列をデータ数×データ数の行列に変換したのちに部分空間法