目的
C++で微分方程式の数値計算をしたい.
結論
オイラー法と4次のルンゲクッタ法について関数を書いた.
template <class Value, class Time, class Function>
auto rungekutta_4th(
const std::valarray <Value> & y, Time t, Time dt, Function && f
) -> std::valarray <Value>
{
auto k1 = f(t, y);
auto k2 = f(t + dt / 2.0, y + k1 * (dt / 2.0));
auto k3 = f(t + dt / 2.0, y + k2 * (dt / 2.0));
auto k4 = f(t + dt, y + k3 * dt);
return (k1 + (k2 * 2.0) + (k3 * 2.0) + k4) * (dt / 6.0);
}
template <class Value, class Time, class Function>
auto euler(
const std::valarray <Value> & y, Time t, Time dt, Function && f
) -> std::valarray <Value>
{
return f(t, y) * dt;
}
環境
C++14だよ.コンパイラはvc141を使っているよ.
std::valarray
ベクトルどうしの演算に特化したクラスだよ.なんかあまり普及している感じがない.というか弊研究室ではだれも知らなかった.かなしい.
ベクトルといえばstd::vectorなんだけど,汎用性が高いぶんベクトル計算は苦手みたいだ.std::valarrayだと特化しているだけあって,各種演算子が便利に作られている.
{// std::vectorの場合
std::vector <int> a{0, 1, 2};
std::vector <int> b{0, 2, 4};
// しんどい
auto c = a;
std::transform(
c.begin(), c.end(),
b.begin(),
c.begin(),
[](auto && v1, auto && v2) {
return v1 + v2;
});
}
{// std::valarrayの場合
std::valarray <int> a{0, 1, 2};
std::valarray <int> b{0, 2, 4};
// 直感的
auto c = a + b;
}
微分方程式の数値解析
本日のゲストはこちら,減衰振動に関する微分方程式です.式はバネ-質量-ダンパ系に関するものだけど,これについての詳細は省くよ.あ,○○法みたいな感じで紹介していくんですけど,それがどんな考えのもとに作られたかとかは紹介しないです.たぶんもっと分かりやすく解説してくださる方がいらっしゃると思うので…….
\left\{\begin{array}{}
\frac{dx^2}{d^2t}+2\gamma\frac{dx}{dt}+\omega^2x=0
\qquad; \gamma:減衰率,\omega:角振動数\\
x|_{t=0}=1\\
\frac{dx}{dt}|_{t=0}=0
\end{array}\right.
上の式について,時間tがある値をとるときのバネの長さxを求める.
オイラー法
微分方程式の数値解析法のひとつとして,オイラー法がある.これは最も単純で,時間で微分してるなら時間をかければいいじゃん? である.
さて,
\frac{dx}{dt}=f(t,x)
とおくと,オイラー法の式は
x_{t=t+\Delta t}=x_{t=t}+f(t,x_{t=t})\Delta t
と表せる.
それはそれとして,今回は
\left\{\begin{array}{}
x_1=x\\
x_2=\frac{dx}{dt}
\end{array}\right.
とおくと,もとの式は,
\left\{\begin{array}{}
\frac{dx_2}{dt}+2\gamma x_2+\omega^2x_1=0\\
x_1|_{t=0}=1\\
x_2|_{t=0}=0
\end{array}\right.
と表せる.こいつを整理すると,
\left\{
\begin{array}{}
\frac{x_1}{dt}=x_2\\
\frac{x_2}{dt}=-2\gamma x_2-\omega^2x_1\\
x_1|_{t=0}=1\\
x_2|_{t=0}=0
\end{array}
\right.
となる.さて,これを行列っぽく表す(なんか名前あるんでしょうか?)と,
\left\{
\begin{array}{}
\frac{d}{dt}\begin{bmatrix}x_1\\x_2\end{bmatrix}
=\begin{bmatrix}x_2\\-2\gamma x_2-\omega^2x_1\end{bmatrix}\\
\begin{bmatrix}x_1\\x_2\end{bmatrix}_{t=0}
=\begin{bmatrix}1\\0\end{bmatrix}
\end{array}
\right.
最後に,オイラー法の式にぶちこむと,
\left\{
\begin{array}{}
\begin{bmatrix}x_1\\x_2\end{bmatrix}_{t=t+\Delta t}
=\begin{bmatrix}x_1\\x_2\end{bmatrix}_{t=t}
+\begin{bmatrix}
x_2\\-2\gamma x_2-\omega^2x_1
\end{bmatrix}_{t=t,x=x_{t=t}}
\Delta t\\
\begin{bmatrix}x_1\\x_2\end{bmatrix}_{t=0}
=\begin{bmatrix}1\\0\end{bmatrix}
\end{array}
\right.
とわかる.じゃあ実装します.
# include <valarray>
const auto PI = std::acos(-1.0);
constexpr double DT = 0.1;
constexpr double GAMMA = 0.2;
constexpr double OMEGA = 1.0;
constexpr double TIME = 30.0;
auto f(double t, std::valarray <double> x) -> std::valarray <double>
{
return {
x[1],
-2.0 * GAMMA * x[1] - OMEGA * OMEGA * x[0]
};
}
auto main() -> int
{
std::valarray <double> x{ 1.0, 0.0 };
for (double t = 0.0; t <= TIME; t += DT)
{
x += f(t, x) * DT;
}
}
実装しました.解説します.
定数となるのは*π,Δt*,γ,ω,tなので,
const auto PI = std::acos(-1.0);
constexpr double DT = 0.1;
constexpr double GAMMA = 0.2;
constexpr double OMEGA = 1.0;
constexpr double TIME = 30.0;
と適当に設定します.また,更新する配列に初期条件を入れます.
std::valarray <double> x{ 1.0, 0.0 };
更新式は前の時点tとその状態xが必要であり更新の操作なので,
auto f(double t, std::valarray <double> x) -> std::valarray <double>
{
return {
x[1],
-2.0 * GAMMA * x[1] - OMEGA * OMEGA * x[0]
};
}
のように関数化してやります.あ,今回はtは必要ないわね.
オイラー法の式はf()を使って,
x += f(x) * DT;
と書けます.これを実行すると,横軸t,縦軸xのグラフは,
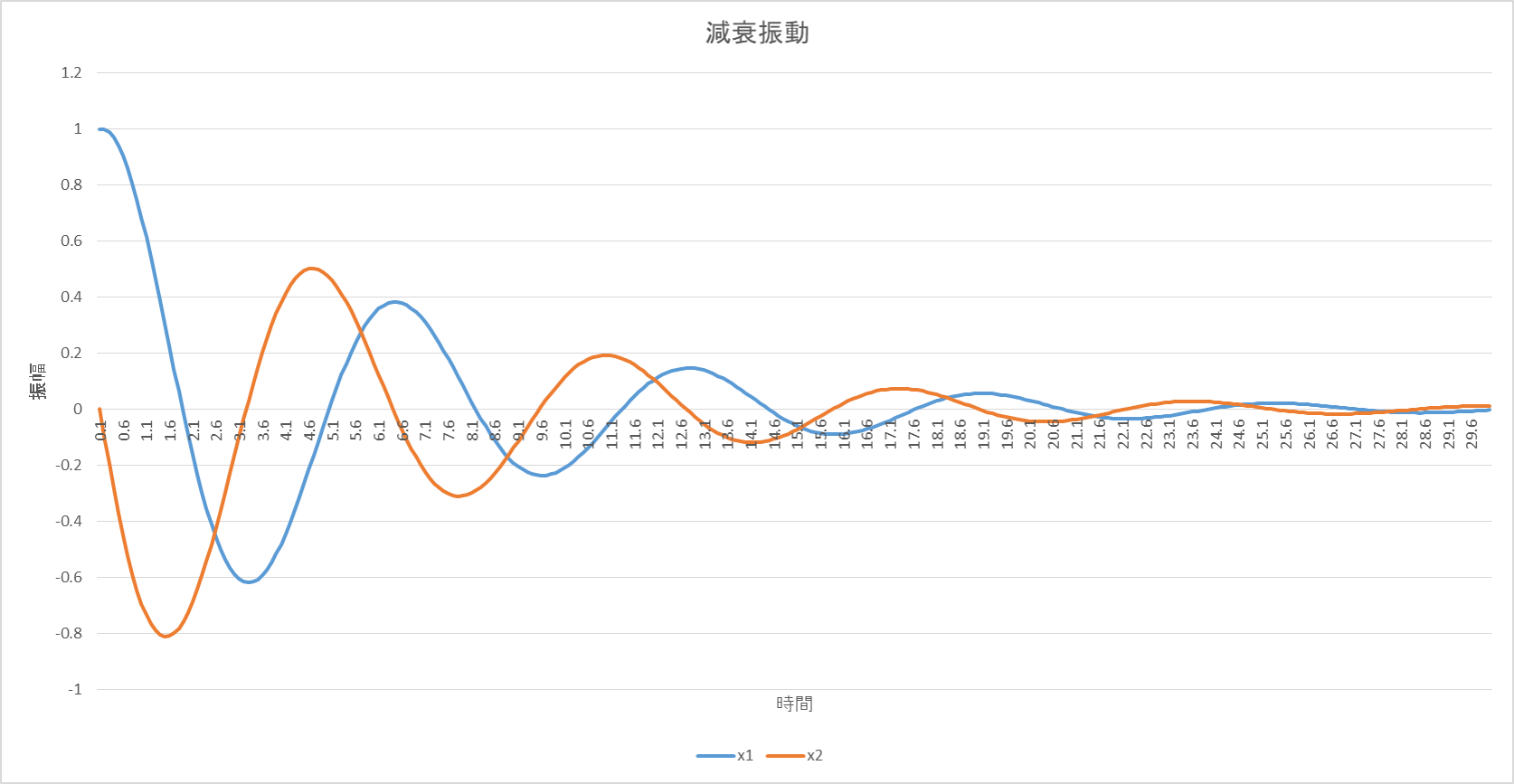
のようになります.青が*x1*なので,これが減衰振動のグラフだよ.
4次のルンゲクッタ法
オイラー法は単純で高速だけど,Δtをそれなりに小さくとらないと誤差がバカにならない.そこで高精度でそこそこ速い数値解法として4次のルンゲクッタ法があるよ.4次があるならってことで1次からn次まであるんだけど,1次はオイラー法と同じだし,5次以降は速度の低下の割に精度が良くならない(つまりコスパが悪い).というわけで今回は4次のルンゲクッタ法だけを実装します.
4次のルンゲクッタ法の式は結構えげつなくて,
\left\{\begin{array}\\
k_1=f(t,x_{t=t})\\
k_2=f(t+\frac{\Delta t}{2},x_{t=t}+k_1\frac{\Delta t}{2})\\
k_3=f(t+\frac{\Delta t}{2},x_{t=t}+k_2\frac{\Delta t}{2})\\
k_4=f(t+\Delta t,x_{t=t}+k_3\Delta t)\\
x_{t=t+\Delta t}=x_{t=t}+(k_1+2k_2+2k_3+k_4)\frac{\Delta t}{6}
\end{array}\right.
となっている.なんじゃこりゃ.少々厄介なところは*k1*から最後まで伝播していることで,このせいで(xのすべての要素が互いに独立している場合を除いて)*kn*を並列に解くことができない.
同じ問題を解くのでオイラー法のときと同様な式変形を行うよ.
じゃあ実装します.
//
// オイラー法のときと同じなのでこのへんは省略
//
auto main() -> int
{
std::valarray <double> x{ 1.0, 0.0 };
for (double t = 0.0; t <= TIME; t += DT)
{
// ここから違う
auto k1 = f(t, x);
auto k2 = f(t + DT / 2.0, x + k1 * (DT / 2.0));
auto k3 = f(t + DT / 2.0, x + k2 * (DT / 2.0));
auto k4 = f(t + DT, x + k3 * DT);
x += (k1 + (k2 * 2.0) + (k3 * 2.0) + k4) * (DT / 6.0);
}
}
実装しました.ほぼ同じだね.
実行するとxの変化は
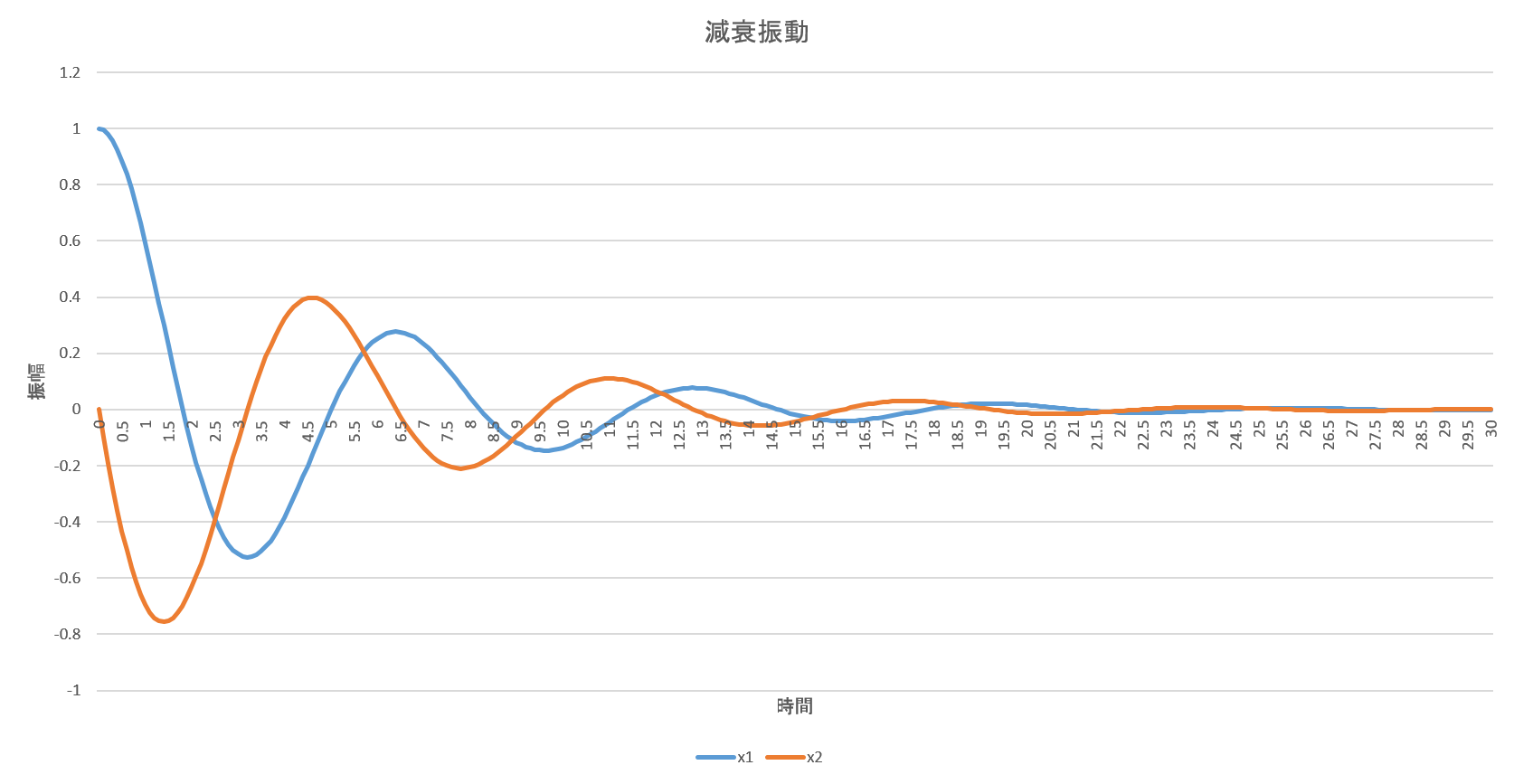
のようになる.当たり前だけど,これもオイラー法のときとほぼ同じ.
関数化する
オイラー法はともかく,4次のルンゲクッタ法を毎回書くのはめんどくさい.関数化しよう.
template <class Value, class Time, class Function>
auto euler(
const std::valarray <Value> & y, Time t, Time dt, Function && f
) -> std::valarray <Value>
{
return f(t, y) * dt;
}
y|t=t+Δtを求めるとき,引数には順に,時点tでの状態y|t=t,時点t,微小時間dt,関数fを入れる.
template <class Value, class Time, class Function>
auto rungekutta_4th(
const std::valarray <Value> & y, Time t, Time dt, Function && f
) -> std::valarray <Value>
{
auto k1 = f(t, y);
auto k2 = f(t + dt / 2.0, y + k1 * (dt / 2.0));
auto k3 = f(t + dt / 2.0, y + k2 * (dt / 2.0));
auto k4 = f(t + dt, y + k3 * dt);
return (k1 + (k2 * 2.0) + (k3 * 2.0) + k4) * (dt / 6.0);
}
こちらも同様.さてこうすると前のコードも少しすっきりする.
auto main() -> int
{
// 定数
const auto PI = std::acos(-1.0);
constexpr double DT = 0.1;
constexpr double GAMMA = 0.2;
constexpr double OMEGA = 1.0;
constexpr double TIME = 30.0;
// 初期値
std::valarray <double> x = { 1.0, 0.0 };
// 更新関数
auto f = [&](auto && t, auto && x) -> std::valarray <double>
{
return {
x[1],
-2.0 * GAMMA * x[1] - OMEGA * OMEGA * x[0]
};
};
// 数値解を求める
for (double t = 0; t <= TIME; t += DT)
{
//x += euler(x, t, DT, f);
x += rungekutta_4th(x, t, DT, f);
}
}