概要
本記事では,大気再解析データからPythonでエマグラムを描画する方法について解説します.
状態曲線だけでなく乾燥断熱線,湿潤断熱線,等飽和混合比線も合わせて描いてみようと思います.
エマグラムの構成要素
エマグラムは,大気の鉛直方向の安定性を見るときなどに用いられるグラフです.
横軸に気温,縦軸に圧力(対数目盛)をとり,その中には
- 状態曲線
- 露点温度線
- 乾燥断熱線
- 湿潤断熱線
- 等飽和混合比線
という5つの線が描かれます.
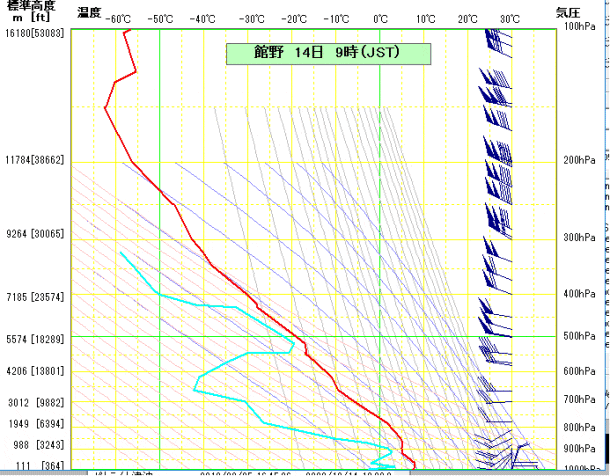
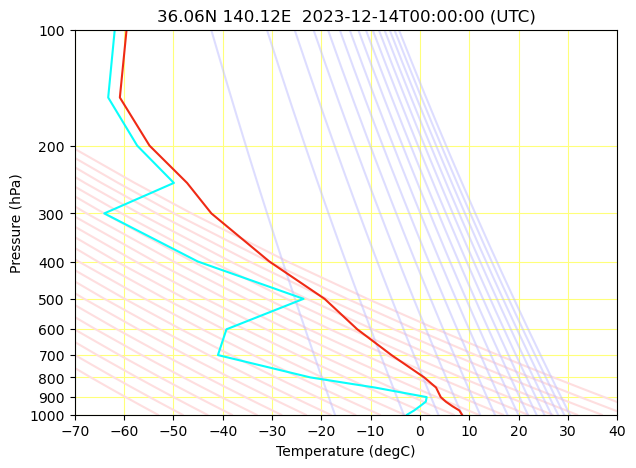
状態曲線は,実際に観測された各高度における気温をプロットしてつなげたグラフのことです.上図の赤線が状態曲線です.
露点温度線は,実際に観測された各高度における気温と相対湿度から算出される露点温度をプロットしたものです.水色の線が露点温度を表しています.
湿度が高いほど気温と露点温度の差は小さくなるので,赤線と水色線が近い高度では空気が湿っているということが読み取れます.
残りの乾燥断熱線,湿潤断熱線,等飽和混合比線は観測値に依らない線です.
青色の線のうち傾きが緩やかな方が,乾燥断熱線です.乾燥した空気塊を断熱的に持ち上げていったときの温度をプロットした線です.乾燥空気を断熱的に持ち上げているということは温位が保存されているので,乾燥断熱線は等温位線ということになります.
薄いピンク色の線は,湿潤断熱線です.今度は水蒸気を含んだ空気塊を断熱的に持ち上げていったときの温度をプロットした線です.等相当温位線と言うこともできます.
青い線のうち傾きが急な方は,等飽和混合比線です.なお,飽和混合比は,飽和水蒸気密度を乾燥空気密度で割った値です.
状態曲線を描く
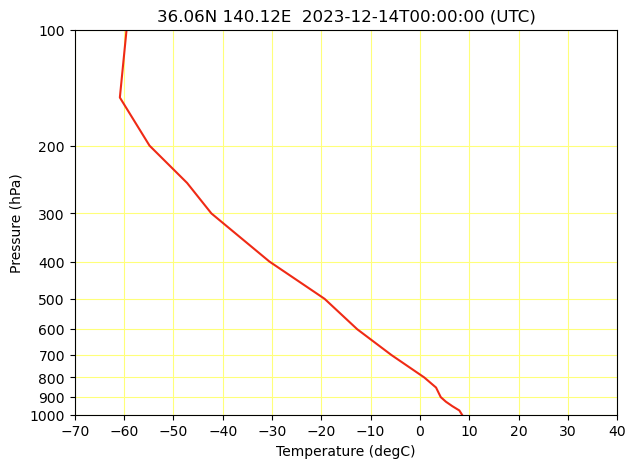
まずは一番簡単な状態曲線から描きます.
データは大気再解析データを使用しました.
データ元:京都大学生存圏研究所のサイト内にある「解析値を中心に再構成したNetCDFデータ」からダウンロード
ファイル場所:MSM-P/2023/1214.nc
1214.ncは100MB以上あるので,必要なデータのみを抽出して1205_temp_rh.ncとして保存
今回は,2023年12月14日9時(日本時間)の館野のエマグラムを描きます.
まずxarrayでNCEPファイルを読み込み,気温データをtempに格納します.
import numpy as np
import matplotlib.pyplot as plt
import xarray as xr
data = xr.open_mfdataset('./1214_temp_rh.nc').load()
# 指定日時・指定位置の気温・相対湿度を取得
TIME = '2023-12-14T00:00:00' # UTC
LAT = 36 + 3.5/60
LON = 140 + 7.5/60
temp = data['temp'].sel(time=TIME, lat=LAT, lon=LON, method='nearest')
rh = data['rh'].sel(time=TIME, lat=LAT, lon=LON, method='nearest')
そうしたらあとはT-logPグラフにプロットするだけです.
# 定数
T0 = 273.15
plt.figure(figsize=(7, 5))
# 状態曲線
plt.plot(temp-T0, np.log10(temp.p), color='#ef2a15')
plt.xlim(-70, 40)
plt.ylim(np.log10(100), np.log10(1000))
plt.xticks(np.arange(-70, 41, 10))
plt.yticks(np.log10(np.arange(100, 1100, 100)), np.arange(100, 1100, 100))
plt.xlabel('Temperature (degC)')
plt.ylabel('Pressure (hPa)')
plt.title(f'{LAT:.2f}N {LON:.2f}E {TIME} (UTC)')
plt.grid(color='#ffff7a')
plt.gca().invert_yaxis()
plt.show()
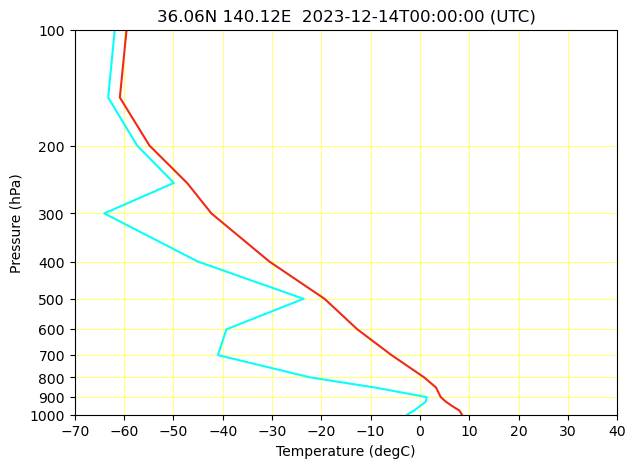
露点温度線を描く
次に,露点温度をプロットします.露点温度は次の式で求められます.
T_d(T,RH) = \frac{1}{\frac{1}{T_0} - \frac{R_v}{L}\log\left(\frac{e_s(T)\frac{RH}{100}}{e_{s0}}\right)}\tag{1}
ここで$T_0$は摂氏0度における絶対温度[K],$R_v$は水蒸気の気体定数[J/K・kg],$L$は蒸発潜熱[J/kg],$e_s(T)$は飽和水蒸気圧[hPa],$e_{s0}$は絶対温度$T_0$における飽和水蒸気圧(観測値)です.なお飽和水蒸気圧$e_s(T)$は次式で表されます.
e_s(T) = e_{s0}\exp\left(\frac{L}{R_v}\left(\frac{1}{T_0}-\frac{1}{T}\right)\right)\tag{2}
まずはこれらを関数で定義しましょう.
# 定数
T0 = 273.15
Rv = 8.31 / 18.015e-3
e0 = 6.11
L = 2.5e6
Rd = 287
Cp = 1004
eps = Rd/Rv
def es(T):
'''飽和水蒸気圧'''
global e0, L, Rv, T0
return e0 * np.exp((L/Rv) * (1/T0 - 1/T))
def T_dew(T,rh):
'''露点温度'''
e = 0.01*rh * es(T) # 水蒸気圧
return 1/(1/T0 - Rv/L * np.log(e/e0))
そしてこれを使って露点温度をプロットします.先ほどの可視化部分に下記を加えるだけです.
# 状態曲線
plt.plot(temp-T0, np.log10(temp.p), color='#ef2a15')
乾燥断熱線を描く
次は乾燥断熱線,すなわち等温位線を描きます.
温位$\theta$は次式で表されます.
\theta(p,T) = T\left(\frac{1000}{p}\right)^{R/C_p}\tag{3}
T-Pグラフに描画したいので,これを$T$について解きます($p$について解いてもよいがやや面倒).
T(p,\theta) = \theta\left(\frac{p}{1000}\right)^{R/C_p}\tag{4}
これを関数で定義して,描画してみます.
def T(p,theta):
'''温位と圧力から気温を計算する'''
global Rd, Cp
return theta*(p/1000)**(Rd/Cp)
可視化は,以下のコードを追記します.
# 乾燥断熱線(等温位線)
for theta in np.arange(220, 325, 5):
plt.plot(T(temp.p, theta)-T0, np.log10(temp.p), color='#fededf')
等飽和混合比線を描く
次は等飽和混合比線です.飽和混合比$q_s$は次式で表されます.
q_s(p,T) = \frac{R_d}{R_v}\frac{e_s(T)}{p-e_s(T)} \equiv \epsilon\frac{e_s(T)}{p-e_s(T)}
ここで$R_d$は乾燥空気の気体定数[J/K・kg],$R_v$は水蒸気の気体定数[J/K・kg],$e_s(T)$は飽和水蒸気圧[hPa]です.$e_s(T)$の表式は式$(2)$を参照してください.
等温位線を描いた時と同様に,この式を$p$について解きます($T$について解くのは難しい).
P(T,q_s) = \frac{\epsilon+q_s}{q_s}e_s(T)
これを関数で定義します.
def P(T,qs):
'''気温と混合比から圧力を計算する'''
global eps
return es(T)*(eps + qs) / qs
可視化部分に以下のコードを追記して描画します.
# 等飽和混合比線
for qs_ in np.arange(0.001, 0.03, 0.002):
T_ = np.arange(-70, 40, 0.1)
plt.plot(T_, np.log10(P(T_+T0, qs_)), color='#bdbdff', alpha=0.5)
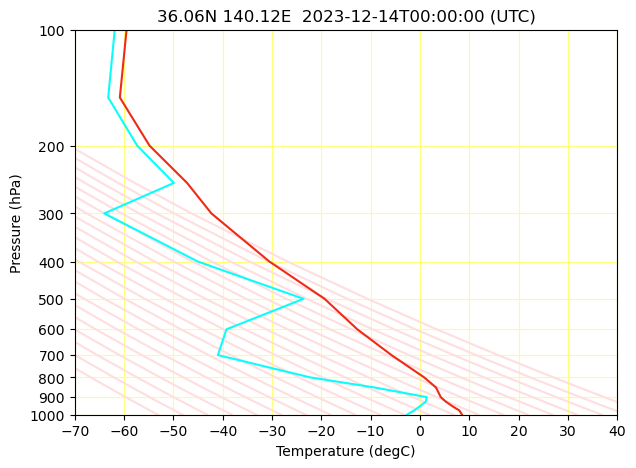
湿潤断熱線を描く
最後に,湿潤断熱線を描きます.湿潤断熱線はちょっとややこしいです.
湿潤断熱線は等相当温位線なのですが,相当温位$\theta_e$は
\theta_e(p,T,RH) = \theta(p,T)\exp\left(\frac{L\cdot q_s(p,T)}{C_p\cdot T_d(T,RH)}\right)
となりますが,これを$p$や$T$で解くのは難しいです.なのであきらめて,湿潤断熱減率$dT/dp$の式
\frac{dT}{dp} = \frac{\frac{R_dT}{C_p} + \frac{Lq_s}{C_p}}{P(1 + \frac{\epsilon L^2 q_s}{C_p R_d T^2})}
をRunge-Kuttaで積分することで$(T,p)$を求めました.
まず$dT/dp$を関数dTdpで定義します.
def qs(p,T):
'''飽和混合比'''
global eps
return eps * es(T) / (p - es(T))
def dTdp(p,T):
'''気温の鉛直勾配(湿潤大気)'''
global Rd, Cp, L, eps
return (Rd*T + L*qs(p,T)) / (p*Cp*(1 + eps*L**2*qs(p,T)/(Cp*Rd*T**2)))
Runge-Kuttaはscipyのライブラリを使うことができます.
from scipy.integrate import solve_ivp
sol.yに温度Tが,sol.tに圧力pが格納されるので,これを使ってプロットします.
# 湿潤断熱線
for T_ in np.arange(0+T0, 40+T0, 5):
sol = solve_ivp(dTdp, t_span=[1000,100], y0=[T_], t_eval=np.linspace(1000,100))
plt.plot(sol.y[0]-T0, np.log10(sol.t), color='#bdbdff')
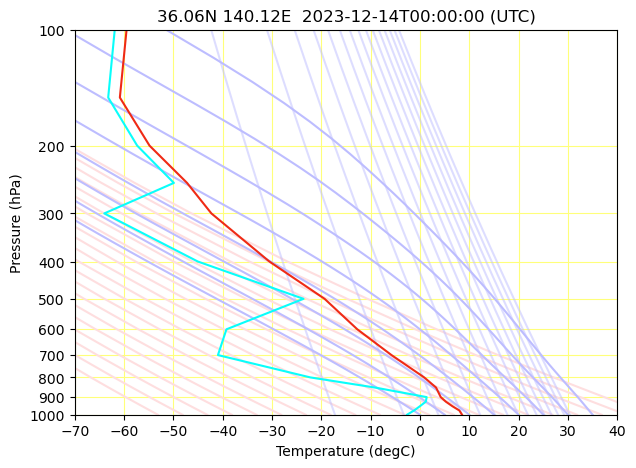
これで完成です!答えと見比べてみましょう.
こちらはゾンデ観測データゆえ大気再解析データの方が粗いのは置いておくとして,概ね合っているのではないかと思います!
参考にしたサイト・ソースコード
今回登場した式は,こちらのサイトから引用しました.
導出に興味のある方は参考にしてみてください.
Qiitaアドベントカレンダーで使ったコードはこちらのレポジトリにまとめています.
本記事のコードは11-emagramの中に入っています.