概要
シリーズ「気象データで時系列解析」では、気象データを例に時系列解析の基礎を学びます。
今回は、定常性について扱います。
定常性とは
定常性には大きく2つあって、弱定常と強定常があります。
弱定常の定義
系列$\{y_t\}$が弱定常であるとは、
- ある$\mu$が存在して、任意の$t$に対し$E[y_t]=\mu$
- 任意の$k$に対しある$\gamma_k$が存在して、任意の$t$に対し$\text{Cov}[y_t,y_{t-k}]=\gamma_k$
を満たすことです。
つまり、平均と共分散が時刻$t$によらず一定(ただし共分散はラグ$k$に依存してよい)であるような系列のことです。
グラフで見ると、ある平均値まわりをずーっと同じ振れ方でギザギザしているような感じになります
単に「定常性」と言ったときは、この弱定常を指すことが多いです。
強定常の定義
一方、系列$\{y_t\}$が強定常であるとは、
- 任意の$k$に対して、$y_{t_1},\cdots,y_{t_n}$の同時分布が$y_{t_1+k},\cdots,y_{t_n+k}$の同時分布に等しい
を満たすことです。
なお、系列の分散が有限なら「強定常⇒弱定常」が成り立ちます。
定常性はどこで使うか
定常性は時系列モデルにおいて基本となる概念で、時系列データを統計的モデルにあてはめる際にしばしば定常性の仮定が必要となります。
例えば、MAモデルという時系列モデルは定常性を仮定しています。
気温データを例に見てみる
定常性のイメージをつかむために、気象庁の「過去の気象データダウンロード」から取得したデータを可視化してみます。
- 地点:京都
- 期間:2022年11月26日~2023年11月26日
- データの種類:時別値
生データは非定常
下図は、京都における1年間の気温をプロットしたものです。
赤線は全期間にわたる平均値です。
可視化のためのコード
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('temperature.csv', encoding='shift-jis', skiprows=3)
df.columns = ['datetime', 'temp']
df['datetime'] = pd.to_datetime(df['datetime'])
plt.figure(figsize=(15,4))
plt.plot(df['datetime'], df['temp'])
plt.xlabel('datetime')
plt.ylabel('temperature')
plt.axhline(y=df.temp.mean(), color='red', linestyle='--')
plt.grid()
plt.show()
明らかにこれは非定常です。
なぜなら気温は季節によって当然異なり、「平均値が時刻$t$に依らず一定」という弱定常の条件を満たさないからです。
階差系列(差分系列)
上で見たように、気温データは非定常でした。
時系列モデルで気温の予測をしたかったのですが、定常性が仮定できないのでもうあきらめるしかないのでしょうか?
いいえ、そんなことはありません。少し手を加えれば定常なデータを作ることができます。
"差分をとる"
ことをやってみましょう。
つまり、
$$y_1-y_0,y_2-y_1,\cdots,y_{t}-y_{t-1},\cdots$$
を計算してみます。Pandasならdiff()メソッドが使えます。
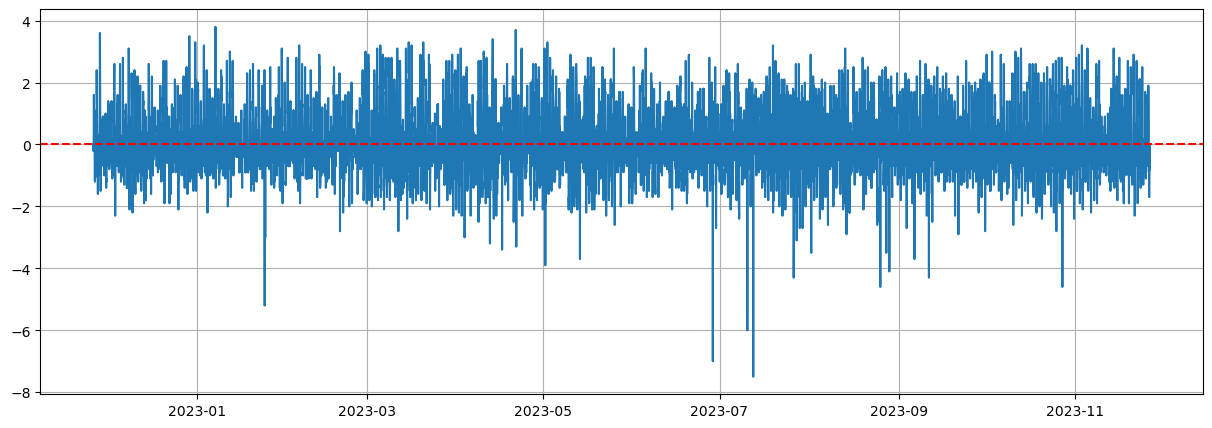
差分を取ったデータをプロットした結果が下図です。
平均はほぼゼロで、その周りを同じような振れ方で振動しています。
なんとなくですが、定常な感じがします。
定常性の検定 -- ディッキー・フラー検定
「なんとなく定常な感じがする」と言いましたが、「なんとなく」では説得力に欠けます。定常性を検定する手法に「ディッキー・フラー検定」というものがあるので、こちらを紹介します。
厳密には、ディッキー・フラー検定は「自己回帰モデルが単位根を持つかどうか」を調べるものです。
1次の自己回帰(AR)モデルとは、系列$\{y_t\}$が次式で表されるようなモデルです。
$$y_t=\phi_1 \cdot y_{t-1} + \epsilon_t$$
$\phi_1$は定数、$\epsilon_t$は誤差項(ホワイトノイズ)です。
このモデルにおいて係数$\phi_1=1$のとき、このモデルは「単位根を持つ」といいます。
単位根を持つとき($\phi_1=1$)、ARモデルはランダムウォークとなりますが、ランダムウォークは非定常です。一方で単位根を持たないとき($|\phi_1|<1$)、ARモデルは定常過程であることが示せます。
なので$\phi_1=1$を帰無仮説として検定をして、棄却されれば定常過程であることがわかるというわけです。
※今回は"1次"の自己回帰モデルで説明しましたが、n次でも同じようなことが言えます。
Pythonでディッキー・フラー検定をするにはstatsmodelsが便利です。
from statsmodels.tsa.stattools import adfuller
result = adfuller(df_diff.dropna()) # df_diffには1次差分の値が格納されている
print(f'ADF statistic: {result[0]}')
print(f'p-value: {result[1]}')
print(f'Critical values: {result[4]}')
ADF statisticは検定統計量の値で、p-valueはP値、Critical valuesは有意水準1%・5%・10%における検定統計量の値が表示されます。
ADF statistic: -20.69795056999495
p-value: 0.0
Critical values: {'1%': -3.431097226246283, '5%': -2.8618702243759544, '10%': -2.56694577346149}
差分系列に対してディッキー・フラー検定を行った結果は上記のとおりです。
帰無仮説は棄却されたので、定常性を持つと言ってよいでしょう。
ソースコード
使ったコードは下記リンクのGitHubに置いてあります。
今回コードは01-JMA_data_analytics/01_stationarity.ipynbです。