本記事は,京都大学人工知能研究会KaiRAのAdvent Calender 8日目の記事です.
概要
ニューラルネットワークの過学習を抑制する方法として代表的なのが,Dropout(ドロップアウト)と呼ばれる手法です.
この記事のメインテーマであるDropConnect(ドロップコネクト)は,Dropoutを一般化した手法です.
DropConnectを提案した以下の論文などを参考にしながら,解説していきます.
前提
ここでは,入力を$v=(v_1,v_2,\cdots,v_n)\top$,出力を$r=(r_1,r_2,\cdots,r_d)^\top$とする1層の全結合層を持つ,次式のようなニューラルネットワークを考えます.
r = a(v) = a(Wv) \tag{1}
ここで$a(\cdot)$は活性化関数(もちろん非線形な関数),$W\in\mathbb{R}^{d\times n}$はニューラルネットワークのパラメータです.ただし$W$にはバイアスも含んでおり,$v_n$は常に1とします.
Dropoutとは何だったか
Dropoutはニューラルネットワークにおける過学習に対する対策として,2012年にHintonらの論文で提案されたものです.
Dropoutでは層の各ノードを,確率$p$で残し,確率$1−p$で消します(ゼロにする).
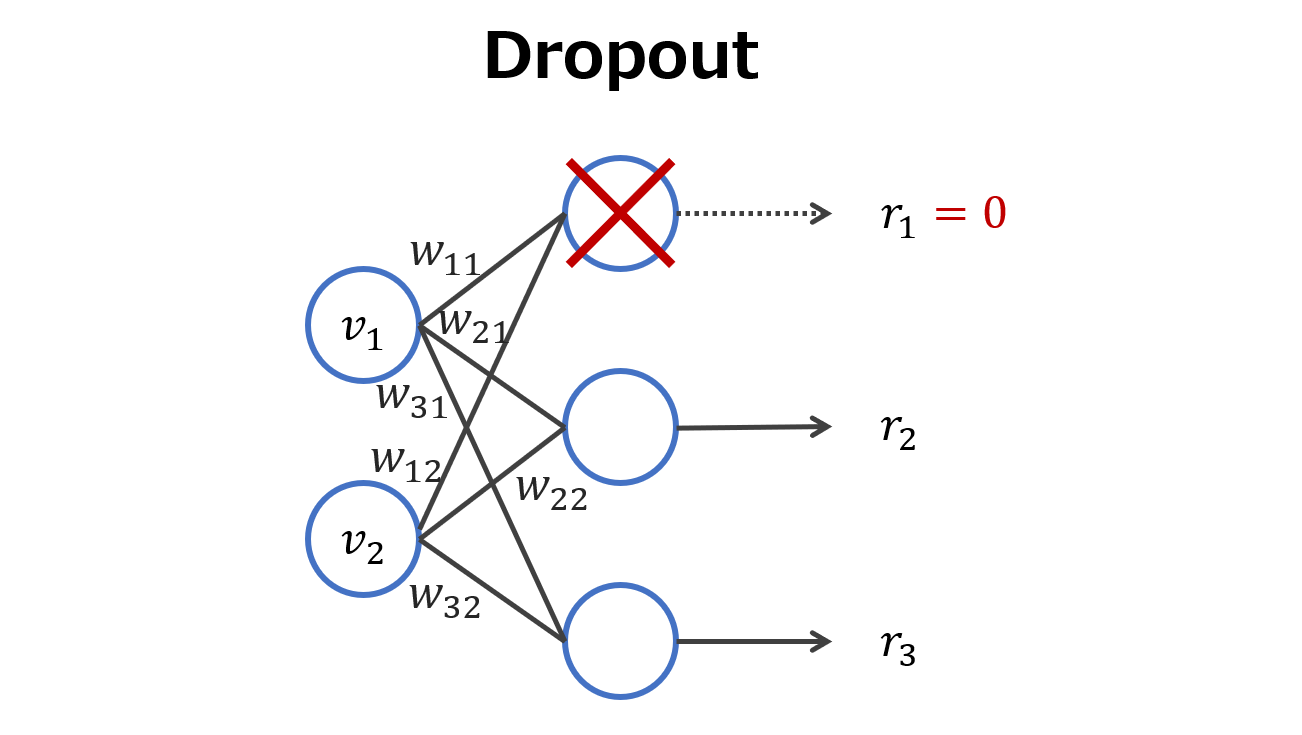
今考えているニューラルネットワーク$(1)$で,中間層と出力層の間にDropoutを挟んだ場合は下図のようになります.
中間層からの出力のうち,$p=2/3$を残し,$1−p=1/3$をゼロにしています.
このことを数式で書くと,次式のようになります.
r = m * a(Wv) \tag{2}
ここで$m\in\mathbb{R}^d$は要素がすべて0 or 1であるマスクベクトルで,$*$は要素ごとの積を表します.出力値に対して1を掛ければそのノードは生き残ることになるし,0を掛ければそのノードは死んだことになるわけですね.
なお,Dropoutでは生き残るノードと死ぬノードを確率的に決めるので,$m$の各要素$m_j\ (j=1,\cdots,d)$はベルヌーイ分布に従います.
m_j\sim Bernoulli(p)
このサンプリング処理は,論文の実装ではForward計算ごとに行っているようです(論文内Algorithm 1を参照).
【本題】DropConnectとは
Dropoutではノード(出力値)を消していましたが,DropConnectではエッジ(重み)を消します.
名前のとおりですね.
- Dropout:outputを消す
- DropConnect:connectionを消す
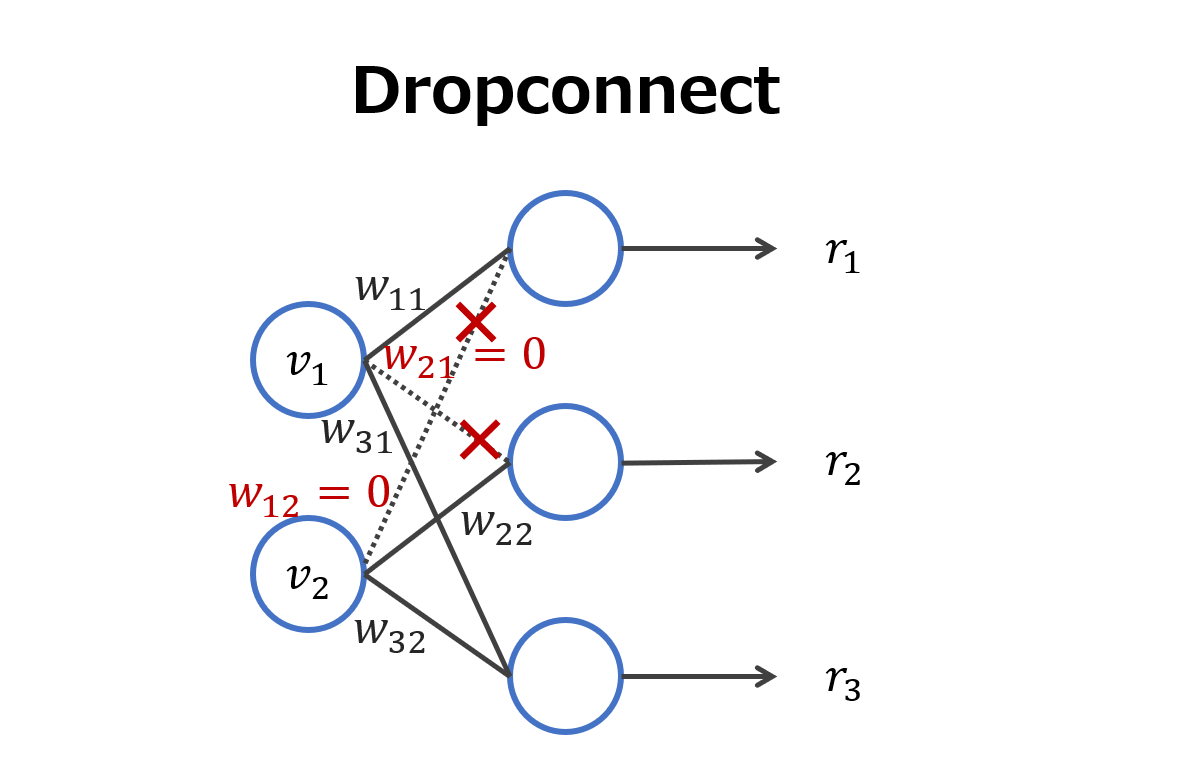
イメージはこんな感じです.
数式で表すと,次式のようになります.
r = a((M*W)v) \tag{3}
$M\in\mathbb{R}^{d\times n}$はすべての要素が0 or 1であるマスク行列で,$*$は要素ごとの積です.Dropoutと同じ考え方で,重み$W$の要素に1が掛かればその重みは生き残り,0が掛かればその重みは死ぬことになります.
またDropout同様,$M$の要素はベルヌーイ分布に従います.
ところで上の図で$w_{11}=w_{21}=0$とし,その他は生き残してやるとどうなるでしょうか?
※ただし,活性化関数はReLUやtanhなどのように$a(0)=0$であるとします.
実は,結局Dropoutと同じことになります.なぜなら,
r_1 = a(w_{11}v_1 + w_{21}v_2) = a(0\cdot v_1 + 0\cdot v_2) = a(0) = 0
となり,1番上のノードが消えていることになるからです.
これが「DropConnectはDropoutの一般化」と冒頭で述べた理由です.
推論時はどうするか
今まで述べてきたのは,学習時の話です.
推論するときにはすべてのノード(エッジ)を使用するのですが,「すべてのノード(エッジ)を使う」だけでは不十分です.なぜなら,学習時は割合$p$のノード(エッジ)でbackpropagationを行っている一方,推論時は割合1のノード(エッジ)を使っているため余計な大きい値が出力されてしまいます.
よって,学習時と推論時で「出力の濃さ」を揃えてあげる必要があります(学習時は出力が"薄い",推論時は出力が"濃い"です).
そこで,「学習時を濃くする」or「推論時を薄くする」の2択があるわけですが,PyTorchのtorch.nn.Dropoutの実装では「学習時を濃くする」を採用しています.つまり,$\frac{1}{1-p}$を出力に対して学習時にかけているということです.
実装
残念ながら,PyTorchでDropConnectを実装するには手動でやるしかなさそうです.
※nn.Dropout()はあります.
import torch
import torch.nn.functional as F
class DropConnect:
def __init__(self, layer, drop_rate=0.5):
self.drop_rate = drop_rate
self.layer = layer
self.mask = None
def forward(self, x, training=True):
if training and (0.0<self.drop_rate<1.0):
keep_rate = 1.0 - self.drop_rate
W = self.layer.weight
t = torch.rand_like(W).to(W.device)
t += keep_rate
mask = t.floor()
dropped_W = mask * W
x = F.linear(x, dropped_W, self.layer.bias)
return x
else:
return x
使い方は単純で,
class MLPClassifier(nn.Module):
def __init__(self, drop_rate):
....
self.fc1 = nn.Linear(784, 256)
self.dropconnect1 = DropConnect(self.fc1, drop_rate)
...
という感じです.