はじめに
ずいぶん昔の記事ですが、Arduinoで家庭の消費電力を計測する素晴らしい記事、
こちらの記事を参考にハードを制作し、スケッチを修正した上で実際に運用しています。
しかし、このような自作の計測機器の場合、本当に正しい値が得られているのかという疑問が常についてまわります。
そこで、Arduinoによる測定結果とスマートメーターから取得した電力情報を1ヶ月に渡って比較してみました。
すると、なかなか良い結果を得ることができたのでご紹介します。
ハードウェアの解説
電力の計算方法は、分電盤のL1,L2電圧線について、瞬時電圧と瞬時電流を Arduino の ADC によって取得し、それらを掛け合わせることで瞬時電力を求めます。複数の瞬時電力を取った上でその平均を電力とする方式です。いかに多くのサンプルを高速で精密に取得できるかが鍵となります。誤差やノイズの影響が考えられるので得られた値の検証が必要です。
以下はセンサーの回路図です。(クランプダイオードやバリスタ、ヒューズなどの安全対策は省略しています。)

Arduino Pro Mini は5V16MHzタイプです。Pro Miniでなくても16MHz以上であれば問題ないと思いますが、ATMega328Pを前提に話を進めています。
Arduino の ADC(アナログ・デジタル・コンバータ)は負の電圧を取得できないため、抵抗R1とR2で $V_{cc}$ の中間にあたる基準電圧$V_{ref}$を作り、この電位を仮想グランドとして交流の正負電圧を測ります。この電圧は常に2.5V付近にあるはずですが、様々な要因で変動することが考えられるので Arduino の A0 ピンに接続しサンプルごとに毎回計測します。この ADC の読み取り値(10bit)を $V_{ref}^a$ とすると 、
V_{ref} = \frac{V_{cc}}{2^{10}}V_{ref}^a \tag{1}
と計算できます。ここで、$V_{cc}$ は Arduino の電源電圧(5V)です。 $2^{10} = 1024$ という数値は 10bit のADCが取りうる値の範囲を表していて、実際に、analogRead()関数は 0 〜 1023 までの値を返します。つまり、0V〜5Vの電圧を1024段階で表すということになります。 $V_{cc}$ はいつも正確に5Vであるとは限らず測定誤差の原因になることに注意が必要です。
次に100Vの交流電圧については、まずトランスTR1(HP-515)によって5V程度の交流に変換されます。しかし5Vというのは定格の負荷がある場合の話で、無負荷の場合は6V程度はあります。実効値で6Vですからピーク電圧は $\pm 6 \times \sqrt{2} = \pm 8.5$[V]で、振幅は17V程度あることになります。これを、さらに R3, R4 で $\pm 8.5 \times 1/(1+4.7) = \pm 1.5$[V]に減圧して仮想グランドの$V_{ref}=2.5$[V]へシフトした電圧を Arduino の A1 に入力しています。
(注:ここではHP-515を使っていますが電圧センシング専用のトランスがあるそうです)
100V交流電源の瞬時電圧を $V_{inst}$、ADCの読み取り値を $V_{inst}^a$ 、トランスと抵抗分圧による減圧分をもとに戻すための増幅率を$G$とすると、
V_{inst} = \frac{V_{cc}G}{2^{10}}(V_{inst}^a - V_{ref}^a) \tag{2}
と計算できます。Gの値はトランスの特性に左右されるため、実測しながら調整するとよいのですが、トランスの出力電圧が6Vだと仮定すると、理論上 G=95となります。上記回路図の通りに制作した場合は、とりあえずG=95としてもそこそこ良い結果になると思います。
次に電流を検出する方法としては、交流電流センサ CTL-10-CLSを用います。クランプ式で電線を中に通すようにはさんでカチッと留めるだけで、交流電流の変化を電圧の変化に変換することができるセンサです。L線(黒)とK線(白)が出ていて、そこに抵抗負荷をつなぎますが、抵抗の大きさによって計測できる電流の範囲を変えることができます。データシートの出力電圧特性を見ると、一般家庭の電流を測るのであれば、100Ωの抵抗負荷が適切であるとわかります。100Ωのラインを見ると0.1A〜50A程度までほぼ直線の特性となっているため、測ろうとする電流がその範囲内であればセンサ電圧の値にパラメーターをかけ合わせるだけで電流値を計算できます。また負荷が100Ωのとき、結合定数Kの特性グラフからK=1.0であることがわかります。
CTL-10-CLSの資料によればCTセンサの巻数 $N$、負荷抵抗 $R_L$、結合定数 $K$ のとき、出力電圧 $E_0$ と貫通電流 $I_0$ の関係は以下の式で表されます。
E_0 = \frac{KR_L}{N}I_0 \tag{3}
これを変形すれば、
I_0 = \frac{N}{KR_L}E_0 \tag{4}
となり、$E_0$を ADC で測定することによって電流値 $I_0$ が計算できることがわかります。したがって、CTLセンサの電圧のADC値を $E_0^a$ とすると、
I_0 = \frac{V_{cc}N}{2^{10}KR_L}(E_0^a - V_{ref}^a) \tag{5}
となります。
トランスに入力するAC電圧(コンセントプラグ)と、L1、L2に取り付けるCT1、CT2にはすべて方向があるので注意が必要です。基準となるのはL1(赤)です。CTセンサーにはK→Lという矢印が記入されているので、L1では電源側(電柱側)がKになるように取り付けます。一方、L2(黒)はL1と逆位相なので、CTセンサーをL1とは逆向きに取り付けることで位相が揃います。また、トランスのL側はL1のL(電圧線)側か、L2であればN(ニュートラル)側に合わせる必要があります。マイナスの出力が出たらプラグを逆に接続すれば良いともいえます。間違えてはならないのはL1とL2のCTセンサーは逆向きに取り付けるという点です。
ハードウェアの特性
次に実際に動作させたときの特性について紹介しておきます。A0をグランドにしたときのA1とA2の波形を以下に示します。

黄色がA1で交流電源の電圧を示しています。100Vの交流がトランスと抵抗分圧で減圧したものを計測しています。これを見ると山の先端の形が多少歪んでいます。原因はよくわかりませんが、使っているトランスの HP-515 が交流電圧測定用の専用品ではないことと、おまけにセンタータップから取り出したことが関係しているような気がします。あるいはオシロスコープがおかしいのかもしれません。もっともこの程度であれば家庭の電力を測りたいという用途であればそれほど大きな問題にはならないと思います。
青はCTセンサの出力電圧で、クランプしている電線に流れる交流電流の大きさの変化を表しています。170W程度の温熱ヒーターを接続している状態です。若干、歪みが見られますが比較的きれいなサイン波になっているようです。ところがこのヒーターのスイッチを操作して弱運転にしてみたところ、以下のような波形になりました。
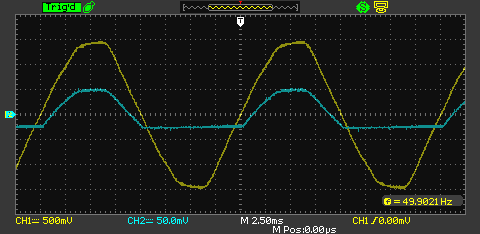
この温熱ヒーターは単純なつくりで弱運転の操作スイッチもスライド式の物理タイプです。波形から推測すると、おそらくダイオードでマイナス側の電流を遮断しているのではないかと思われます。しかし、見ての通り波形全体がマイナス側に移動しているためマイナス側の電流が流れているように見えています。これでは正しい電流値や電力値を得ることができないと思います。使用する電気機器の制御の方法しだいで電流の直流成分が発生するとCTセンサーでは正しい電流が計測できなくなるということだと思いますが、筆者はあまり詳しくないためこれ以上の考察は控えます。
とにかく、このような特性があることを確認した上でスマートメーターのデータとの比較を進めてゆきます。
ADコンバータの速度
まず最初に検討する必要があるのは Arduino の ADCの速度です。一般家庭に電力会社から供給されている電源は東日本が50Hz、西日本が60Hzの実効値100Vの交流です。交流の1周期に要する時間はそれぞれ、
東日本 : 1 \div 50 = 0.02 [s] = 20,000 [\mu s]\\
西日本 : 1 \div 60 = 0.016667 [s] = 16,667 [\mu s]
となります。ADCの速度の問題とは、商用電源の1周期をさらに50分割して各点の電圧や電流を測ることができるかということです。 50という数には明確な根拠はありませんが、それくらいあれば良いかなという感覚的な判断です。元記事では25としていました。なお、瞬時電力を求めるためには電圧用に1ch、電流用に2ch、そして基準電圧の1ch で合計4ch の ADC が少なくとも必要なので4chをすべて計測するものとします。
ATMega328P のデータシートを見ると、ADCクロックが50kHz〜200kHzのときに最大分解能での変換が可能であるとの記載があります。このADCクロックはシステムクロックを分周して生成されていて、デフォルトで128分周、つまり16MHzの Arduino の場合、16MHz ÷ 128 = 125 kHz となります。したがってデフォルトでは最大分解能で変換できているわけです。またADCが終了するまでに必要なクロック数については、初回のADCが25クロック、次回以後は13クロックかかるとのことです。したがって、1度のADCにかかる時間は、
\frac{1}{16} \times 128 \times 13 = 104 [\mu s]
となります。
さらに、1周期あたり50サンプルで、4ch分を得ようとすると、すべてのサンプリングにかかる時間は、
104 \times 50 \times 4 = 20,800 [\mu s]
となります。この結果は 50Hzの1サイクルである 20,000 を少し超えており、1周期50サンプル×4chのADCは不可能であるとの結論を得ます。
しかし、ADC クロックの分周比はデフォルトで128ですが、これを変更することができます。設定可能な分周比は 2, 4, 8, 16, 32, 64, 128 で、値が小さいほうが速くなりますがその分精度が悪くなるということです。64か32で検討してみます。それぞれの分周比について、商用電源の1周期を50サンプル×4chで取得する場合にかかる時間を表にまとめてみると、
| 分周比 | 128 | 64 | 32 |
|---|---|---|---|
| ADCクロック[kHz] | 125 | 250 | 500 |
| 1クロック時間[us] | 8 | 4 | 2 |
| ADC1回の時間[us] | 104 | 52 | 26 |
| 50サンプル×4chの時間[us] | 20800 | 10400 | 5200 |
となります。当然といえば当然ですが2倍ずつ速くなっています。なお、ここで得られた時間は最低限必要な時間であり、ATMega328Pを使う限りはこれよりも短くはならないという意味です。実際にはこの時間に加えてプログラム上のオーバーヘッドや、その他の処理時間も必要です。
では、実際どれほどの時間がかかるのか実験で確かめてみしょう。
ADC速度のテスト
環境: Arduino Pro mini 5V 16MHz
電源の1周期あたり50サンプルを取得するためには、東日本(50Hz)の場合、周期20,000usを50で割った400usごとにADCを実行する必要があります。西日本(60Hz)の場合は333usごととなります。
以下に示すテストコードではTimer1割り込みを使って400usごとに4ch分のADCと必要な計算を行うコールバック関数を呼び出しています。メインループでは1秒ごとにデータの内容を読み出してSerialに送信し変数をクリアしています。
また、動作チェックのためADC実行関数の開始時に outPin の出力レベルを HIGHに、終了時に LOW にしています。
このピンの状態をオシロスコープで観測すればADC実行部の時間を測ることができます。
# include <TimerOne.h>
// ピンの定義
const int RPin = 0; // 仮想グランドとなる基準電圧(A0)
const int VPin = 1; // 交流電圧用(A1)
const int CPinA = 2; // L1電流CTセンサ用(A2)
const int CPinB = 3; // L2電流CTセンサ用(A3)
const int outPin = 2; // 動作チェック出力ピン(D2)
const int intcycle = 400; // 割り込み周期 400us (50サンプル/周期)
// 変数の定義
long sumIVA, sumIVB; // 電流*電圧(ADC値)の積算
long sumV, sumIA, sumIB; // 電圧、電流(ADC値)の自乗の積算
int samples; // サンプル数カウンタ
// タイマー割り込みで400usごとに呼び出されるADC実行部
// ここで行うのは ADC の実行と必要最小限の計算
void callback_adc() {
digitalWrite(outPin, HIGH); // 動作チェック用
int vref = analogRead(RPin);
int v0 = analogRead(VPin);
int Ea0 = analogRead(CPinA);
int Eb0 = analogRead(CPinB);
long v = (v0 - vref); // 電圧のADC値を基準電圧を中心にシフト(正負値に戻す)
sumV += v * v;
long Ea = (Ea0 - vref);
sumIVA += Ea * v;
sumIA += Ea * Ea;
long Eb = (Eb0 - vref);
sumIVB += Eb * v;
sumIB += Eb * Eb;
samples++;
digitalWrite(outPin, LOW); // 動作チェック用
}
void setup() {
Serial.begin(19200);
// ADCSRA レジスタの下位3ビットで分周比を指定する
// 0b101->32, 0b110->64
ADCSRA = ADCSRA & 0b11111000;
ADCSRA = ADCSRA | 0b101;
delay(1000);
pinMode(outPin, OUTPUT);
Timer1.initialize(intcycle);
Timer1.attachInterrupt(callback_adc);
samples = 0;
}
void loop() {
# とりあえずなにか表示して進捗確認
Serial.print(sumIVA);
Serial.print(", ");
Serial.print(sumIVB);
Serial.print(", ");
Serial.println(samples);
sumV = 0.0;
sumIVA = 0.0;
sumIA = 0.0;
sumIVB = 0.0;
sumIB = 0.0;
samples = 0;
delay(1000);
}
ADCの分周比を設定するために、setup() 内で ADCSRA レジスタの値を書き換えています。このレジスタの下位3bitがADCクロックの分周比を指定する部分です。詳細はデータシートで確認していただくとして、0b101が32分周で、0b110が64分周です。
以下の画像は、この2つの設定で上のプログラムを実際に動作させて outPin の状態をオシロスコープで見た結果です。
32分周の場合、

エッジの立ち上がりから立ち下がりまでの時間は148.6usと計測されました。
一方64分周の場合は、
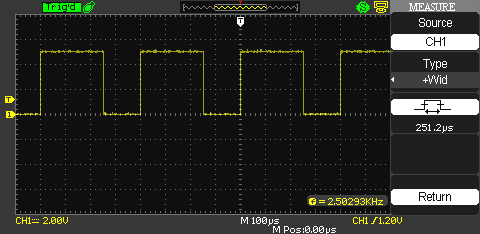
251.2usとなりました。148.6の2倍まではかかっていません。1回のADCに要する最小時間は64分周の場合は52usで、4chのADCで204usはかかるはずです。よって、251-204=47usが他の処理(計算やオーバーヘッド)ということになります。32分周の場合は26×4=104で 149-104=45usがそれにあたり、予想通りほぼ等しくなっています。ちなみに、16分周の場合は93-52=41usでした。(少し小さくなる傾向??)
ところで、64分周の場合、割り込み処理時間はサンプリング周期内に収まってはいるものの、CPUの半分以上を使っていることがわかります。割り込み処理がCPUを占有してしまうと電力の計算やシリアル通信部などプログラムの他の部分の実行に影響が大きくなるので、64ではなく32で進めたいと思います。ADCの精度が落ちるとのことですが、スマートメーターから取得したデータと比較することで、実用に耐えるものかどうか判断する方針とします。
ちなみに、サンプリング数が50の場合は以下のようなサンプリング密度となります。これが適切であるかどうか正直わかりませんが、とりあえずこれでやってみることにします。

実効電圧の計算
実効電圧 $V_{rms}$ は、サンプリングした瞬時電圧 $V_{inst}$ の自乗平均の平方根で近似することができます。ここで$M$はサンプル数とします。
\begin{eqnarray}
V_{rms} &=& \sqrt{\frac{{\sum^{M}} {V_{inst}}^2}{M}} \tag{6}
\end{eqnarray}
式(2)より、
V_{inst} = \frac{V_{cc}G}{2^{10}}(V_{inst}^a - V_{ref}^a)
だったので、これを式(6)に代入すると、
\begin{eqnarray}
V_{rms} &=& \sqrt{\frac{{\sum^{M}} {V_{cc}}^2 G^2(V_{inst}^a - V_{ref}^a)^2}{(2^{10})^2 M}} \\
&=& \frac{V_{cc} G}{2^{10}} \sqrt{\frac{{\sum^{M}} (V_{inst}^a - V_{ref}^a)^2}{M}}\tag{7}
\end{eqnarray}
先ほどのテストコードの中では、変数 sumV が、$\sum^M (V_{inst}^a - V_{ref}^a)^2$ で、samples が $M$に該当します。よって、実効電圧Vrmsを計算するコードは以下のようになります。
float Vcc = 5.0;
float G = 95.0;
float vcoeff = Vcc * G / 1024.0;
float Vrms = vcoeff * sqrt(float(sumV)/samples);
実効電流の計算
実効電圧と同様、実効電流 $I_{rms}$ は、サンプリングした瞬時電流 $I_{inst}$ の自乗平均の平方根で近似できます。
\begin{eqnarray}
I_{rms} &=& \sqrt{\frac{{\sum^{M}} {I_{inst}}^2}{M}} \tag{8}
\end{eqnarray}
式(5)より、
I_0 = \frac{V_{cc}N}{2^{10}KR_L}(E_0^a - V_{ref}^a)
であり、$I_0 = I_{inst}$ なので、これを式(8)に代入すれば、
\begin{eqnarray}
I_{rms} &=& \frac{V_{cc}N}{2^{10}KR_L} \sqrt{\frac{{\sum^{M}} (E_0^a - V_{ref}^a)^2}{M}} \tag{9}
\end{eqnarray}
テストコードでは、sumIA, sumIB が $\sum^{M}(E_0^a - V_{ref}^a)^2$ に該当するので、実効電流 IrmsA, IrmsB を計算するコードは以下のようになります。
float N = 3000.0;
float RL = 100.0;
float K = 1.00;
float icoeff = Vcc * N / (1024.0 * K * R);
float IrmsA = icoeff * sqrt(float(sumIA)/samples);
float IrmsB = icoeff * sqrt(float(sumIB)/samples);
電力の計算
さきほどの温熱ヒーターの例からも分かるように、電流の変化は必ずしもサイン波となるわけではありません。例えば次の図はノートPCのACアダプタに流れる電流を測ったものですが、このような様々な成分を含む複雑な波形となる場合もあります。

各時点における瞬時電圧 $V_{inst}$ と瞬時電流 $I_{inst}$ についてはこれまで述べてきましたが、これらをかけ合わせたものが瞬時電力 $W_{inst}$ となります。
\begin{eqnarray}
W_{inst} &=& V_{inst} \times I_{inst}\\
&=& \frac{V_{cc}G}{2^{10}}(V_{inst}^a - V_{ref}^a) \times \frac{V_{cc}N}{2^{10}KR_L}(E_0^a - V_{ref}^a)\\
&=& \frac{V_{cc} G}{2^{10}} \bullet \frac{V_{cc} G N}{2^{10} K R_L}(V_{inst}^a - V_{ref}^a)(E_0^a - V_{ref}^a)\tag{10}
\end{eqnarray}
ここでは、一定時間内にサンプリングによって得られた瞬時電力の平均を有効電力として扱います。したがって、電力 $W$ は、
\begin{eqnarray}
W &=& \frac{\sum^M W_{inst}}{M} \\
&=& \frac{V_{cc} G}{2^{10}} \bullet \frac{V_{cc} G N}{2^{10} K R_L} \frac{\sum^M (V_{inst}^a - V_{ref}^a)(E_0^a - V_{ref}^a)}{M}\tag{11}
\end{eqnarray}
となります。
テストコードでは、sumIVA、sumIVB が $\sum^M (V_{inst}^a - V_{ref}^a)(E_0^a - V_{ref}^a)$ に該当します。 したがって、電力値 WattA, WattB を計算するコードは以下のようになります。
float wcoeff = vcoeff * icoeff;
float WattA = wcoeff * float(sumIVA) /samples;
float WattB = wcoeff * float(sumIVB) /samples;
ここで少し注意が必要です。太陽光発電などで売電を行う場合は、逆潮流といいますが電流の向きが逆になる(電流の位相が電圧の位相の反対になる)ことがあり、その場合はマイナスの電力が計算されてきます。テストコードのように sumIV に積算してゆくような計算方法だと、サンプリング時間が長くなるとプラスとマイナスが打ち消し合ってしまう可能性があります。スマートメーターは売電の量もカウントしていてデータとして取得できるのですが、筆者は売電をしていないため、どういう時間単位でマイナスとプラスを分けて積算しているのか知りません。理論的には1周期(1/50 秒)ごとにプラスかマイナスかを判定すると良いのでしょうが、今回は簡単に1秒(50周期)ごとに計算することにしています。何れにせよ売電時の逆潮流は無いため、ゼロ付近での誤差以外でマイナスの電力が出力されることはありません。
スマートメーターデータとの比較
以下にスマートメーターの電力情報と、今回の Arduion の計測結果を同じグラフに表示した例を2日分示します。


L1, L2 は Arduino で計測した WattA、WattB の10分平均です。また BROUTE はスマートメータの瞬時電力を10秒ごとに取得して10分平均を出したものです。2つの系列はグラフ上で見ればほぼ一致していることがわかります。
L1L2積算電力は WattA、 WattBを午前0時を起点に積算して電力量を求めたものです。またBR積算電力はスマートメーターから積算電力量データを取得し、午前0時の最初の積算電力量データからの差分をとったものです。これらの系列もグラフ上でまずまずの一致を見せています。
以上4系列について、1ヶ月分比較してみたのが次の表になります。
| 日付 | L1+L2平均 | BROUTE平均 | 誤差(%) | L1L2積算電力 | BR積算電力 | 誤差(%) |
|---|---|---|---|---|---|---|
| 11/01 | 838.2 | 834.8 | 0.4% | 20.0 | 19.6 | 2.0% |
| 11/02 | 933.4 | 922.2 | 1.2% | 22.2 | 21.8 | 1.8% |
| 11/03 | 969.4 | 963.2 | 0.6% | 23.1 | 22.7 | 1.8% |
| 11/04 | 913.7 | 902.1 | 1.3% | 21.8 | 21.4 | 1.9% |
| 11/05 | 934.9 | 921.7 | 1.4% | 22.3 | 21.8 | 2.3% |
| 11/06 | 895.1 | 897.7 | -0.3% | 21.3 | 20.9 | 1.9% |
| 11/07 | 941.6 | 933.1 | 0.9% | 22.4 | 21.9 | 2.3% |
| 11/08 | 968.6 | 959.9 | 0.9% | 23.1 | 22.6 | 2.2% |
| 11/09 | 952.9 | 946.9 | 0.6% | 22.7 | 22.3 | 1.8% |
| 11/10 | 856.3 | 846.4 | 1.2% | 20.4 | 20.1 | 1.5% |
| 11/11 | 1061.6 | 1047.4 | 1.4% | 25.3 | 24.8 | 2.0% |
| 11/12 | 754.8 | 749.2 | 0.7% | 18.0 | 17.7 | 1.7% |
| 11/13 | 995.3 | 987.2 | 0.8% | 23.7 | 23.3 | 1.7% |
| 11/14 | 856.3 | 855.8 | 0.1% | 20.4 | 20.0 | 2.0% |
| 11/15 | 1043.6 | 1032.4 | 1.1% | 24.9 | 24.3 | 2.5% |
| 11/16 | 905.1 | 891.7 | 1.5% | 21.6 | 21.2 | 1.9% |
| 11/17 | 834.9 | 828.3 | 0.8% | 19.9 | 19.5 | 2.1% |
| 11/18 | 1022.5 | 1013.7 | 0.9% | 24.4 | 23.8 | 2.5% |
| 11/19 | 916.3 | 910.6 | 0.6% | 21.8 | 21.4 | 1.9% |
| 11/20 | 1070.8 | 1061.9 | 0.8% | 25.5 | 24.9 | 2.4% |
| 11/21 | 1079.0 | 1068.4 | 1.0% | 25.7 | 25.3 | 1.6% |
| 11/22 | 1063.6 | 1050.5 | 1.2% | 25.3 | 24.9 | 1.6% |
| 11/23 | 1054.8 | 1054.8 | 0.0% | 25.1 | 24.4 | 2.9% |
| 11/24 | 967.4 | 955.9 | 1.2% | 23.1 | 22.5 | 2.7% |
| 11/25 | 886.7 | 887.8 | -0.1% | 20.5 | 21.0 | -2.4% |
| 11/26 | 1133.7 | 1120.6 | 1.2% | 27.0 | 26.6 | 1.5% |
| 11/27 | 1019.3 | 1013.0 | 0.6% | 24.1 | 23.8 | 1.3% |
| 11/28 | 1253.2 | 1243.7 | 0.8% | 29.4 | 29.2 | 0.7% |
| 11/29 | 1170.1 | 1157.4 | 1.1% | 26.9 | 27.3 | -1.5% |
| 11/30 | 861.3 | 853.1 | 1.0% | 20.5 | 20.2 | 1.5% |
この表を見ると、arduinoの方がスマートメーターよりも若干大きめな値になっていることがわかります。もう少しパラメーターを調整すればスマートメーターに近づけることもできますが、自宅の電力を見える化するという程度の用途であれば全く問題ないレベルにあると言えます。
おわりに
今回の検証を通して、Arduino のような安価なマイコンを使って家庭での実用的なレベルで電力を計測することができることがわかりました。実はもっと以前から Arduino による計測は行っていたのですが、DIYレベルではその値の正しさを検証する有効な方法がありませんでした。Bルートによる電力の取得が可能になったことで今回の検証ができたわけですが、皮肉にもそのおかげで存在意義を失いつつあります。
とはいえ、Bルートによるスマートメーターへの問い合わせは、返答が戻ってくるまで1,2秒かかります。1秒毎に問い合わせるのはどうかと思いますし、電波の有効利用の観点からも必要以上の問い合わせは控えるべきだと思います。 Arduino + CT電流センサーを用いれば1秒ごとに電力状況を更新するような表示器を作ることも可能になります。また、特定の電気系統や電気製品だけにしぼって計測することもできるので、応用の幅は広がります。
最後に、本記事は実効電圧、実効電流など技術的な内容を含んでいますが、筆者は専門家ではなく勉強した内容をまとめたに過ぎません。もし誤りや勘違いがあることにお気づきの方はぜひともご指摘いただければ幸いです。