概要
Dual-pivot quicksort ベース + 3 way partition でメモリ転送回数の増加を抑えつつ、ワークメモリを併用することで高速な安定ソートを実装してみました。いくつかの高速化のアイディアを導入することで乱数データなどで一般的なクイックソート実装(3つのメディアン・5つのメディアン)に対してやや速い程度のパフォーマンスとなりました。ちなみにワークメモリは作業配列と同サイズが必要になります。
(Intel Core i7 3770K 3.5GHz 定格運転で独自のベンチマークテストに基いた結果。異なるテストでは異なる結果になる可能性もあります。)
今回これを mmsSort と名付けました。
アルゴリズム解説
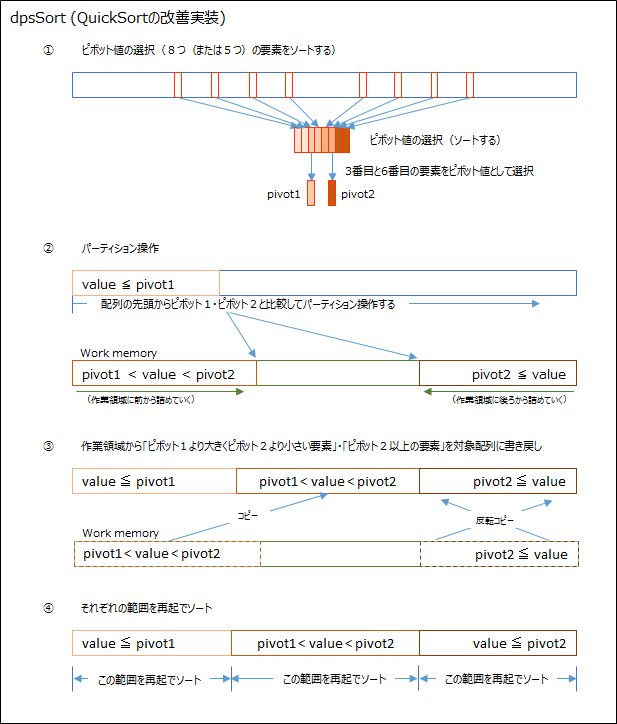
1.ソート対象から適当に8(要素数が小さい場合は5個)取り出してソートし、3番目と6番目(または2番目と4番目)をピボット値として採用します。
2.ソート対象を先頭から走査し、次のように振り分けます。
ピボット1以下の値(value≦pivot1)はソート対象の先頭から詰めていきます。
ピボット2以上の値(pivot2≦value)は作業領域の後ろから前方向に詰めていきます。
ピボット1より大きく、ピボット2より小さい値(pivot1<value<pivot2)は作業領域の前方から後ろ方向に詰めていきます。
3.作業領域の「pivot1<value<pivot2」と「pivot2≦value」をソート対象の「value≦pivot1」の後ろに追加します。
(「pivot2≦value」は順序を反転してコピーします)
4.「pivot2≦value」・「pivot1<value<pivot2」・「value≦pivot1」をそれぞれ再起でソートします。
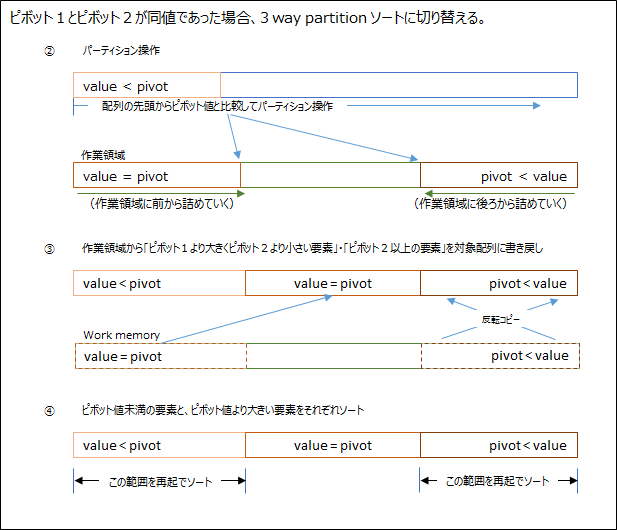
もし、1番目のピボットの選択で、ピボット1とピボット2が同じ値の場合は、3 way partition アルゴリズムに切り替えます。
アルゴリズム図解
ベンチマーク結果
乱数/ユニーク乱数/前半ソート済み・後半ランダム/昇順ソート済み/降順ソート済み/全て同値で計測を行いました。
乱数/ユニーク乱数でクイックソートをやや上回る結果を得ました。10,000,000件の乱数データで以下のような結果となりました。
mmsSort : 2.626秒
Quick Sort (Median of 5) : 2.748秒 (mmsSort の 1.046倍)
Quick Sort (Median of 3) : 2.848秒 (mmsSort の 1.084倍)
※ベンチマークの信頼性については、後述します。
一方、昇順ソート済み/降順ソート済みはあまり良くない結果となりました。一般的なクイックソートでは、昇順ソート済みは全くメモリ転送が発生しません。降順ソート済みも初回のパーティション操作のみメモリ転送が発生し、この時点で(ほぼ)ソート済みとなるため、ほとんどメモリ転送が発生せず、乱数データよりかなり高速化します。これに対し mmsSortでは、通常時と同じようにメモリ転送が発生してしまうため乱数データと同程度の計算量となり、良くない結果になってしまったようです。ちなみに、前半ソート済み・後半ランダム/昇順ソート済み/降順ソート済みはマージソート系のアルゴリズムがとても高速に動作します。
比較回数に関しては、mmsSortは一般的なクイックソート系アルゴリズムと同じくらいかやや少ないくらいとなりました。ただし比較回数は、一般的にクイックソート系のアルゴリズムよりマージソート系のアルゴリズムのほうが概ね少なくなっています。このことは、メモリ転送が高速で、あまりこれがネックにならない場合や比較関数が重い処理の場合などで、マージソートのほうがクイックソートより速くなる可能性があることを示します。(比較のキーが文字列でありかつロケールを考慮しなければいけなかったり、ハッシュオブジェクトからの値の取り出しなど、比較関数が重くなるケースは多いかもしれません)
ベンチマークでは以下のアルゴリズムの比較を行っています。
- mmsSort
- 今回のお題のアルゴリズム
- mmSort
- 比較回数を抑える改良を施したクイックソート(5つのメディアンベース) …そのうちこれも記事書きます
- [Many Pivot Sort](http://qiita.com/matsu_boolean/items/99ffbc2814c3e1fdc649)
- 事前に大量のピボット値を用意することで高速化したアルゴリズム
- Quick Sort
- 一般的なクイックソート実装(ピボット値は配列の中央位置固定)
- Quick Sort (Median of 3)
- 一般的なクイックソート実装(ピボット値は3つの要素の中央値)
- Quick Sort (Median of 5)
- 一般的なクイックソート実装(ピボット値は5つの要素の中央値)
- Quick Sort (3 Way & Median of 5)
- クイックソート(3 way partition)実装(ピボット値は5つの要素の中央値)
- MasSort
- 高速化版マージソート …そのうちこれも記事書くかも…書かないかも
- MatSort
- ワークメモリを少なくできる改良版マージソート …そのうちこれも記事書きます
- Merge Sort
- 一般的なマージソート実装
- Arrays.Sort
- Arraysクラスのsortメソッド(JDK 8のため、TimSort実装)
統計学的解析
mmsSortと、QuickSort (Median of 5), QuickSort (Median of 3)のベンチマーク結果に対しT検定を行ってみました。
結果は以下の通り、p <0.05 となり有意な結果を得ました。効果量 d についても共に十分に大きな値を得ることができました。
テスト条件は以下の通り
要素数 : 10,000,000
配列タイプ : 乱数 (10個ずつの重複あり)
サンプル数 : 各々のアルゴリズムごとに20回ずつ実行
実行環境 : java version "1.8.0_40"
Java(TM) SE Runtime Environment (build 1.8.0_40-b25)
Java HotSpot(TM) 64-Bit Server VM (build 25.40-b25, mixed mode)
ハードウェア : Intel Core i7 3770K 3.5GHz (定格運転)
mmsSortとQuickSort (Median of 5)の比較
mmsSort
平均 : 2.6256 秒
標準偏差 : 0.06377
QuickSort (Median of 5)
平均 : 2.7482 秒
標準偏差 : 0.06377
T検定
p=7.46552E-05 (p<0.05)
効果量
d=1.40044488
mmsSortとQuickSort (Median of 3)の比較
mmsSort
平均 : 2.6256 秒
標準偏差 : 0.06377
QuickSort
平均 : 2.8482 秒
標準偏差 : 0.04854
T検定
p=1.86193E-14 (p<0.05)
効果量
d=3.927094512
最後に
今回作成したアルゴリズム、mmsSortはクイックソートとマージソートの中間程度のパフォーマンスを想定して設計しましたが、実装を様々に最適化することでクイックソートをやや上回る結果を得ることができました。ただし、比較回数はマージソート系に劣るし、昇順ソート済み・降順ソート済みデータに対しては他のアルゴリズムのほうが良好な結果となりました。(mmsSortが遅くなったのではなく、他のアルゴリズムが速くなったため)。
それでも、すべての条件で最速とはいえないまでも安定ソートでありながら、、乱数データ・ユニーク乱数データ等でクイックソート(Median of 3, Median of 5)を上回ることができ、一定の成果を得ることができたと思います。