この投稿の目的
クイックソートやマージソートを改善した、より高速なソートアルゴリズムを書いてみたいなあと思いGitHubに登録したり、こちらに書いてみたりしたのですが、全然誰も見てくれていないようなのでテコ入れに書いてみます。
今回はクイックソートのお話し
クイックソートのおさらい
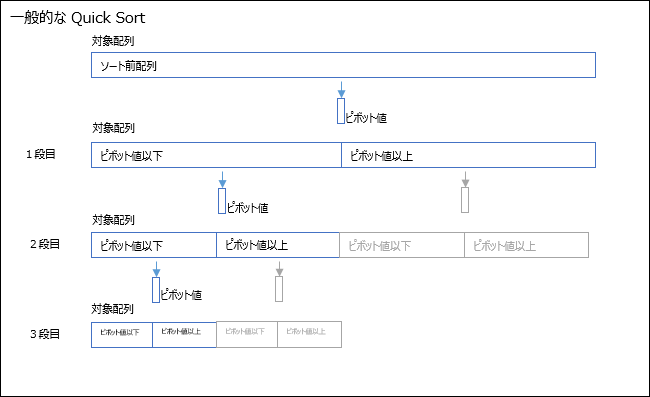
一般的なクイックソートは大体以下のような感じ
1.配列中から基準となる「ピボット値」を決める
2.配列の前半にピボット値以下の値を、後半にピボット値以上の値を集める
3.前半の配列(ピボット値以下の値)をソート、後半の配列(ピボット値以上の値)をソート
Javaで記述したサンプルは以下のような感じ
public static final <T> void quickSort(final T[] array, final int from, final int to, final Comparator<? super T> comparator)
{
final int range = to - from; // ソート範囲サイズ
final T pivot = array[from + range / 2]; // ピボット値(ソート対象の中央位置)
int curFrom = from; // 現在処理中位置の小さい方の位置
int curTo = to - 1; // 現在処理中位置の大きい方の位置
do {
while (comparator.compare(array[curFrom], pivot) < 0) {
curFrom++;
}
while (comparator.compare(pivot, array[curTo]) < 0) {
curTo--;
}
if (curFrom <= curTo) {
final T work = array[curFrom];
array[curFrom] = array[curTo];
array[curTo] = work;
curFrom++;
curTo--;
}
} while (curFrom <= curTo);
if (from < curTo + 1) {
quickSort(array, from, curTo + 1, comparator);
}
if (curFrom < to - 1) {
quickSort(array, curFrom, to, comparator);
}
}
上記のサンプルでは、配列の中央にある値をピボットとして採用している。ただしこれはあまり良くない。QuickSortにおいてピボット値の選択は重要で、パフォーマンスに大きく影響を与える。ピボット値が配列中の値の中で中央値に近い場合、よりベターなパフォーマンスを出し、$O(N log N)$に近くなる。ピボット値として配列中の値の中で最小値や最大値を選択してしまった場合、パフォーマンスは最悪、$O(N^2)$まで落ちる。
一般的には配列中から3つの値を取り出し、その中央値を利用するなどして、パフォーマンス改善を行うことがある(3つのメディアン)が、ここでは別の方法でより良いパフォーマンスを求めてみた。
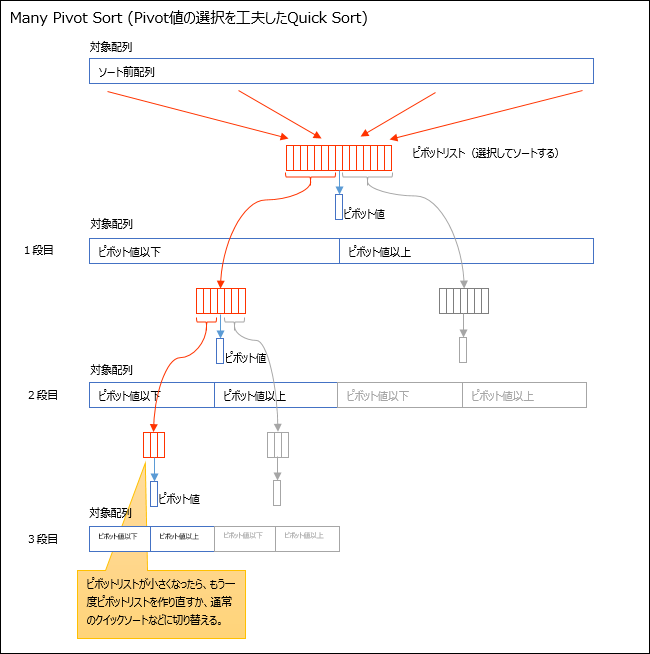
新しいピボット値選択方式 … Many Pivot Sort
新しいピボット値選択方式では、対象配列から事前に非常に多くのピボット候補(ピボットリスト)を選択しておく。こちらの実装では127個のピボットリストを作成する。このピボットリストは事前にソートしておく。このピボットリストの作成とソートは少しコストのかかる処理である。
最初のピボット値選択では、この中央値(63番目)の値を利用する。このピボット値選択は単に配列の中央の添え字から選択するだけであるからほとんどコストはかからない。127個もの中央値であるから、全体の対象配列中でも非常に中央値に近いことが期待できる。このピボット値以下のリスト・ピボット値以上のリストに振り分けた後、再起的手続きでピボット値以下のリスト・ピボット値以上のリストをソートするが、ピボット値以下のリストでは先のピボットリスト0~62番を新しいピボットリストとして使用する。同様にピボット値以上のリストでは先のピボットリスト64~126番を新しいピボットリストとして使用する。
このようにピボットリストを再起するごとに約半分に振り分け、最終的にピボットリストが3つ未満になるまで使いまわす。3つ未満になった場合は、一般的な3つのメディアンより選択性が悪くなるので、再度対象配列から127個のピボットリストを作り直す。
protected static final <T> void mpSort(final T[] array, final int from, final int to, final T[] pivots, final int fromPivots, final int toPivots, final Comparator<? super T> comparator)
{
final int pivotIdx = fromPivots + (toPivots - fromPivots) / 2; // using index from pivots (center position) / pivots配列の中で、今回使うべき要素の添え字
final T pivot = pivots[pivotIdx]; // pivot value / ピボット値
int curFrom = from; // min index / 現在処理中位置の小さい方の位置
int curTo = to - 1; // max index / 現在処理中位置の大きい方の位置
while (true) {
while (comparator.compare(array[curFrom], pivot) < 0)
curFrom++;
while (comparator.compare(pivot, array[curTo]) < 0)
curTo--;
if (curTo < curFrom)
break;
final T work = array[curFrom];
array[curFrom] = array[curTo];
array[curTo] = work;
curFrom++;
curTo--;
}
if (from < curTo) {
if (fromPivots >= pivotIdx - 3) // pivotsの残りが3つを切ったらpivotsを作り直す。(最後まで使い切らないのは、最後の1個は範囲内の中間値に近いとは言えないので)
mpSort(array, from, curTo + 1, comparator);
else
mpSort(array, from, curTo + 1, pivots, fromPivots, pivotIdx, comparator);
}
if (curFrom < to - 1) {
if (pivotIdx + 1 >= toPivots - 3) // pivotsの残りが3つを切ったらpivotsを作り直す。(最後まで使い切らないのは、最後の1個は範囲内の中間値に近いとは言えないので)
mpSort(array, curFrom, to, comparator);
else
mpSort(array, curFrom, to, pivots, pivotIdx + 1, toPivots, comparator);
}
}
public static final <T> void mpSort(final T[] array, final int from, final int to, final Comparator<? super T> comparator)
{
final int range = to - from; // sort range / ソート範囲サイズ
// ソート対象配列サイズが3以下のときは特別扱い
if (range < SWITCH_SIZE) {
// しきい値以下ではクイックソート(3つのメディアン)に切り替える。
QuickSortM3.quickSortMedian3(array, from, to, comparator);
return;
}
int pivotsSize = PIVOTS_SIZE;
@SuppressWarnings("unchecked")
final T[] pivots = (T[])new Object[pivotsSize]; // pivot candidates / ピボット候補の配列
// Selection of the pivot values (Binary insertion sort ish processing).
// ピボット(複数)の選出
for (int i = 0; i < pivots.length; i++) {
pivots[i] = array[(int)(from + (long)range * i / pivots.length + range / 2 / pivots.length)];
}
// sort of pivot candidates / ピボット値のみをソート
BinInsertionSort.binInsertionSort(pivots, 0, pivots.length, comparator);
// sort of array / ソート対象本体のソート
mpSort(array, from, to, pivots, 0, pivots.length, comparator);
}
パフォーマンス
要素数 10,000,000 と 100,000,000 でランダムデータをソートした実行時間と比較関数の呼ばれた回数を記載する。
一般的なQuickSortと比較して、実行時間・比較回数とも 15% 程度改善した。
ランダムデータ (時間:10回実行した平均(秒))
| アルゴリズム | 10,000,000 | 100,000,000 |
|---|---|---|
| Many Pivot Sort | 3.117 | 42.593 |
| Quick Sort (Median of 3) | 3.046 | 44.227 |
| Quick Sort | 3.585 | 49.723 |
ランダムデータ (比較回数:10回実行した平均(回))
| アルゴリズム | 10,000,000 | 100,000,000 |
|---|---|---|
| Many Pivot Sort | 256900851 | 2914248341 |
| Quick Sort (Median of 3) | 284961051 | 3266912797 |
| Quick Sort | 298758228 | 3436000611 |