\newcommand{\deriv}[2]{#1^{(#2)}}
\newcommand{\setN}{\mathbb{N}}
\newcommand{\setR}{\mathbb{R}}
\newcommand{\setC}{\mathbb{C}}
※この記事は,私のブログで執筆した記事『さんすうのーと(3) ―上限・下限』を若干編集し,移植したものです.
はじめに
数学を専門としない工学系の人でもよく見かけると思われる,上限・下限についての解説をしようと思います.
特に,「上限・下限のイメージは分かるけど,具体的にどういう性質を持つかよく分かってない」ような人に向けてこの記事を書いたつもりです.
僕自身,上限・下限のイメージを持ってはいたものの,数学的にどういう性質を持つかきちんと理解していなかったがために少し苦しんだことがありました.
例えば,上限の性質を数式で書き下せないと,証明中でその性質を活かすことができません.
この記事の最後に,上限・下限の性質を活かした証明を載せています.
これを見て頂ければ,直感的な理解だけだとダメなときがあるってことが,少しでも分かってもらえるかと思います.
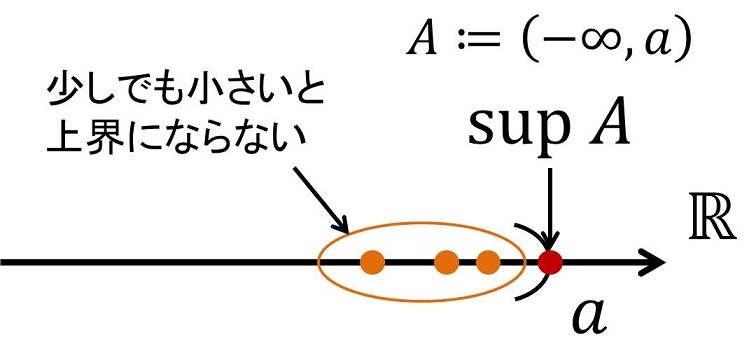
下に上限のイメージ図を載せておきます(下限も同様です).
今回は,このイメージを数式でどう書き下せるかを目標に進めていきます.
上限・下限の性質
(今回は実数体における上限・下限に限って話を進めていきます.)
定義(上限・下限)
空でない集合$~A \subset \setR~$について,$~A~$の上界全体の集合に最小元が存在するとき,その最小元を$~A~$の上限といい,$\sup A$ と表記する.
また,$~A~$の下界全体の集合に最大元が存在するとき,その最大元を$~A~$の下限といい,$\inf A$ と表記する.$\square$
この最小性・最大性から導かれる次の命題が,上限・下限の直感的なイメージを数式で書き下したものになります.
この命題は難しくはないのですが,非常に便利です.
命題 1
$~s \in \setR~$が空でない集合$~A \subset \setR~$の上限となるための必要十分条件は,次の(1),(2)を満たすことである:
(1)$~\forall a \in A,~ a \le s~$
(2)$~\forall x < s,~ \exists a \in A,~ x < a~$
また,$t \in \setR~$が$~A \subset \setR~$の下限となるための必要十分条件は,次の(1'),(2')を満たすことである:
(1')$~\forall a \in A,~ a \ge t~~$
(2')$~\forall x > t,~ \exists a \in A,~ x > a~~$
$\square$
(1)は$~s~$が$~A~$の上界となっていることを言っており,(2)は$~s~$より「少しでも」小さい数を持ってくると,それは絶対に$~A~$の上界とならないことを言っています.
証明
まず,$s = \sup A~$であるときに(1),(2)を満たすことを示す.
$s~$は$~A~$の上界であるから,(1)は明らかに満たす.
また,任意の$~x<s~$なる$~x \in \setR~$をとると,これは$~A~$の上界とはならない.
なぜなら,この$~x~$が$~A~$の上界であったとすると,$~s~$が$~A~$の上界全体の集合の最小元であることに反するからである.
よって,$~x~$が上界でないことから(2)も満たす.
次に,$s \in \setR~$が(1),(2)を満たすときに$~s = \sup A~$であることを示す.
(1)が成り立つので$~s~$は明らかに$~A~$の上界である.
もし,$s~$が$~A~$の上界全体の集合の最小元でないとすると,$~u<s~$なる$~A~$の上界$~u \in \setR~$が存在する.
この$~u~$について,任意の$~a \in A~$に対して$~a \le u~$となるが,これは$~s~$が(2)を満たすことに反する.
よって,$~s~$は$~A~$の上界全体の集合の最小元でないといけない.
つまり,$s = \sup A~$となる.
$t \in \setR~$について,$t = \inf A~$であることと$~t~$が(1'),(2')を満たすことが同値であることは,以上の議論と全く同様にして示されるので,省略する($~s~$を$~t~$に置き換え,不等号を逆にするなど,適宜修正すればよい).$\square$
応用例
実数の連続性の公理で「空でない上に有界な$~\setR~$の部分集合は上限を持つ」というのがありますが,上の命題より「下に有界な部分集合が下限を持つ」ことも分かります.
具体的には次のような命題が成り立ちます.
命題 2
空でなく下に有界な集合$~B \subset \setR~$は下限を持ち,$\inf B = -\sup (-B)~$が成り立つ.
ただし,$-B := \{ -b ~;~ b \in \setR \}~$である.$\square$
証明
$-B~$が上に有界となることから$~\sup (-B)~$が存在する.
$s := \sup (-B)~$とおいて,$\inf B = -s~$となることを示す.
命題 1より,$s~$は次の(1),(2)を満たしている:
(1)$~\forall b \in B,~ -b \le s~$
(2)$~\forall x < s,~ \exists b \in B,~ x < -b$
よって,次の(1'),(2')を満たすことも分かる:
(1')$~\forall b \in B,~ b \ge -s$
(2')$~\forall x > -s,~ \exists b \in B,~ x > b$
よって,再び命題 1より$~\inf B = -s~$が分かる.$\square$
もう少しだけ応用例を挙げてみます1.
#### 定義(Lebesgue外測度)$A \subset \setR$ に対して,$m^*(A)~$を次のように定める:
m^* (A) := \inf \left\{ \sum_{j=1}^\infty |I_j| ~;~ \{I_j\}:開区間の列, \, A \subset \bigcup_{j=1}^\infty I_j \right\}
ここで,$I := (a,b)~$に対して$~|I| := b-a~$としている.
$m^* (A)~$を$~A~$のLebesgue外測度という.$\square$
命題 3
$A_i \subset \setR~(j \in \setN)~$に対して次が成り立つ:
m^* \left( \bigcup_{j=1}^\infty A_j \right) \le \sum_{j=1}^\infty m^*(A_j)
$\square$
証明
任意の$~\varepsilon > 0~$を1つとり,固定する.
外測度の定義と下限の性質(命題 1の(2'))より,任意の$~j \in \setN~$に対し,次を満たす開区間の列$~\{I_{j,k}\}_{k \in \setN}~$が存在する:
A_j \subset \bigcup_{k=1}^\infty I_{j,k}, \quad \sum_{k=1}^\infty |I_{j,k}| < m^*(A_j) + \frac{\varepsilon}{2^j}
$~\{I_{j,k}\}_{k \in \setN}~$は可算個の開区間の集合であり,かつ$~\cup A _j~$の被覆となっている.
さらに,不等式評価を得る:
\sum_{j,k = 1}^\infty |I_{j,k}|
= \sum_{j=1}^\infty \left( \sum_{k=1}^\infty |I_{j,k}| \right)
< \sum_{j=1}^\infty \left( m^*(A_j) + \frac{\varepsilon}{2^j} \right)
= \sum_{j=1}^\infty m^*(A_j) + \varepsilon
よって,外測度の定義より $m^*(\cup A _j) \le \sum |I _{j,k}| < \sum m^ *(A _j) + \varepsilon~$が成り立つ.
$\varepsilon~$は任意であったから,結局$~m ^ * ( \cup A _j ) \le \sum m ^ * ( A _j )~$が成り立つ.$\square$
上の証明中で,一番最初の不等式を得るのに下限の性質を使ってます.
つまり,直感的には次のとおりです:
- 下限の値$~m^* (A_j)~$よりも少し大きい値$~m^* (A_j) + \varepsilon / 2^j~$をとる.
- 下限の性質より$~m^* (A_j) + \varepsilon / 2^j~$は下界にならないので,その数よりも小さい元を集合$~\{ \sum |I_{j,k}| ~;~ A_j \subset \cup I_{j,k} \}~$からとってこれる.
参考文献
- 杉浦光夫,『解析入門 Ⅰ』
- 谷島賢二,『新版 ルベーグ積分と関数解析』
-
『新版 ルベーグ積分と関数解析』のp.17-18より ↩