はじめに
この記事はBrainpad Advent Calendar 2024の5日目になります。
株式会社ブレインパッドでデータサイエンティストをしているまさやです。
今年も新卒1年目の同期と一緒に数理最適化で新卒研修のチーム分けをしました。
去年と同様、今回の最適化問題は特定の最大化ないし最小化したい目的関数があるわけではないので、基本的に制約を満たす実行可能解を見つける問題として定式化します。
23卒版はこちらを是非ご覧ください。
考慮した条件
まず、最適なチームの組合せを考える上で定められた4つの条件を確認します。
| 考慮した条件 | 理由 | |
|---|---|---|
| 1 | 17名を5つのいずれかのチームに割り当てる | 全員にチームを割り当てる |
| 2 | 各チームにリーダー気質のメンバーを1人以上割り当てる | チームを引っ張ってくれる人が欲しい |
| 3 | すべてのチームの分析演習スコアが均一になるようにする | チームごとの技術力を均一にする |
| 4 | 大学時代の専攻を「理学系」「情報系」「社会科学系」の3カテゴリに分けて、それぞれがばらけるようにする | 専攻をばらけさせたい |
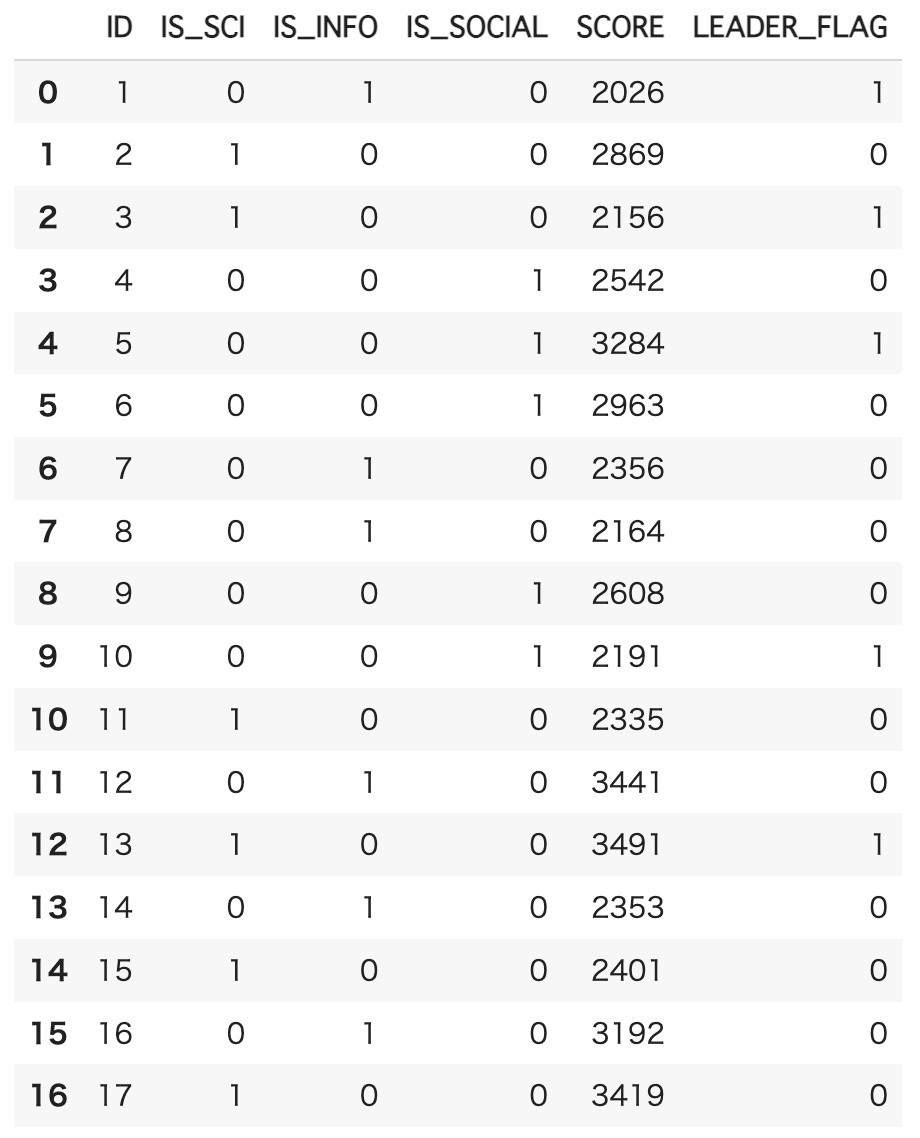
これらをまとめて以下のような入力データを作成します。
また、実装の中で"SCORE"は正規化して処理を行いました。理由としては、値のスケールを他の変数と合わせるためです。
 |
数理モデリング
集合
最初に集合について以下のように定めます。
$I=\{ 1, 2,...,17 \}$ : 人
$J=\{ 1, 2,...,5 \}$ : チーム
$I_{leader}$ : リーダー気質の人
$K = \{ \text{Science, Information, Social} \}$ : 専攻の種別
決定変数
続いて、決定変数を以下のように定めます。
$x_{i,j} \in \{ 0,1 \}$ : 人$i$がチーム$j$に割り当てられるかどうか
$z^{+}_{j}, z^{-}_{j} \in \mathbb{R}_{\geq 0}\ (j\in J)$ : チーム$j$の分析演習スコアの制約に対する違反量を表すスラック変数
$z_k \in \mathbb{R}_{\geq 0}\ (k \in K)$ : 専攻$k$の制約に対する違反量を表すスラック変数
定数
最後に定数について以下のように定めます。
$Score_i\ (i \in I)$ : 人$i$の分析演習スコア
$Score\_average$ : 1チームあたりのスコア平均(= 全員のスコアの和 ÷ チーム数)
$Major_{i,k} \in \{ 0,1 \} \ i \in I,\ k \in K$ : 人$i$が専攻$k$出身かどうか
定式化
上記で定めた集合・決定変数・定数を用いて以下の最適化問題を考えます。
\begin{equation*}
\begin{aligned}
& {\text{minimize}}
& & \sum_{j \in J} (z^{+}_{j} + z^{-}_{j}) + \sum_{k \in K} z_k\\
& \text{subject to}
& & \sum_{j \in J} x_{i,j} = 1, \
&&& ^{\forall}i \in I,\\
& & & \sum_{i \in I} x_{i,j} \geq 3, \
&&& ^{\forall}j \in J, \\
& & & \sum_{i \in I} x_{i,j} \leq 4, \
&&& ^{\forall}j \in J, \\
& & & \sum_{i \in I} Score_i x_{i,j} - Score\_average \geq -z^{-}_{j}, \
&&& ^{\forall}j \in J, \\
& & & \sum_{i \in I} Score_i x_{i,j} - Score\_average \leq z^{+}_{j}, \
&&& ^{\forall}j \in J, \\
& & & \sum_{i \in I_{leader}} x_{i,j} \geq 1, \
&&& ^{\forall}j \in J. \\
& & & \sum_{i \in I} Major_{i,k}x_{i,j} \leq \left\lceil \frac{\sum_{i \in I}
Major_{i,k}}{5} \right\rceil + z_{k}, \
&&& ^{\forall}j \in J, k \in K, \\
& & & z_{j}^{+}, z_{j}^{-} \geq 0, \
&&& ^{\forall}j \in J, \\
& & & x_{i,j} \in \{0, 1\},
&&& ^{\forall}i \in I, j \in J.
\end{aligned}
\end{equation*}
まず、1つ目の制約はハード制約で「メンバーをそれぞれ1つのチームに割り当てる」ことを示しています。また、2, 3番目の制約では、1つのチームが3人以上4人以下を示しています。したがって、1~3番目の制約で「17名を5つのいずれかのチームに割り当てる(4人チームが3つ、3人チームが2つ)」という条件が満たされるようになります。
また、4,5番目の制約では、ソフト制約で違反量を表すスラック変数を用いて「すべてのチームの分析演習スコアが均一になるようにする」という条件を表しています。
6番目の制約では、ハード制約でリーダー気質の人が1チームに1人以上いるようにしています。ここで、リーダー気質の人は最低5人以上(チームの数以上)でないと”Infeasible"(実行不可能)になってしまうので注意してください。
最後に、7番目の制約ではソフト制約で4, 5番目の制約同様に違反量を表すスラック変数を用いて「大学時代の専攻を『理学系』『情報系』『社会科学系』の3カテゴリに分けてそれぞれがばらけるようにする」という条件を表しています。
以上の制約がある上で、違反量を最小化することを目的に解くことで、バランスの取れたチームの組合せを導くことができます。
実装・結果
以上の最適化問題をpulpでモデリングしてソルバーに渡します。
import pulp
import pandas as pd
import numpy as np
import scipy.stats
# データの読み込み
df = pd.read_csv('minipro_opt2024.csv')
# 分析演習のスコアを標準化
df['SCORE_Z'] = scipy.stats.zscore(df['SCORE'])
# 集合
I = df['ID'].to_list()
J = [1, 2, 3, 4, 5]
I_leader = [row.ID for row in df.itertuples() if row.LEADER_FLAG == 1]
K = ['IS_SCI', 'IS_INFO', 'IS_SOCIAL']
# 定数
Score = dict(zip(df['ID'], df['SCORE_Z']))
Score_average = df['SCORE_Z'].sum() / 5
Major = {(i, k): df.loc[df['ID'] == i, k].values[0] for i in I for k in K}
# 問題定義
model = pulp.LpProblem(name='minipro_team', sense=pulp.LpMinimize)
# 決定変数
x = pulp.LpVariable.dicts('x', [(i,j) for i in I for j in J], cat='Binary')
z_plus = pulp.LpVariable.dicts('z_plus', J, cat='Continuous', lowBound=0)
z_minus = pulp.LpVariable.dicts('z_minus', J, cat='Continuous', lowBound=0)
z = pulp.LpVariable.dicts('z', K, cat='Continuous', lowBound=0)
## ハード制約
# メンバーをそれぞれ1つのチームに割り当てる
for i in I:
model += pulp.lpSum(x[i,j] for j in J) == 1
# 各チームには3人か4人割り当てられる
for j in J:
model += pulp.lpSum(x[i,j] for i in I) >= 3
model += pulp.lpSum(x[i,j] for i in I) <= 4
# 1チームに1人以上はリーダー気質の人を割り当てる
for j in J:
model += pulp.lpSum(x[i,j] for i in I_leader) >= 1
## ソフト制約
# チーム毎のスコアの偏りをなくす
for j in J:
model += pulp.lpSum(Score[i]*x[i,j] for i in I) - Score_average >= -z_minus[j]
model += pulp.lpSum(Score[i]*x[i,j] for i in I) - Score_average <= z_plus[j]
# 専攻毎の偏りをなくす
for j in J:
for k in K:
# 大学時代の専攻を『理学系』『情報系』『社会科学系』の3カテゴリに分けてそれぞれがばらけるようにする
model += pulp.lpSum(Major[i,k]*x[i,j] for i in I) <= np.ceil(float(str(pulp.lpSum(Major[i,k] for i in I)/5))) + z[k]
# 目的関数
model += pulp.lpSum(z_plus[j]+z_minus[j] for j in J) + pulp.lpSum(z[k] for k in K)
model.solve()
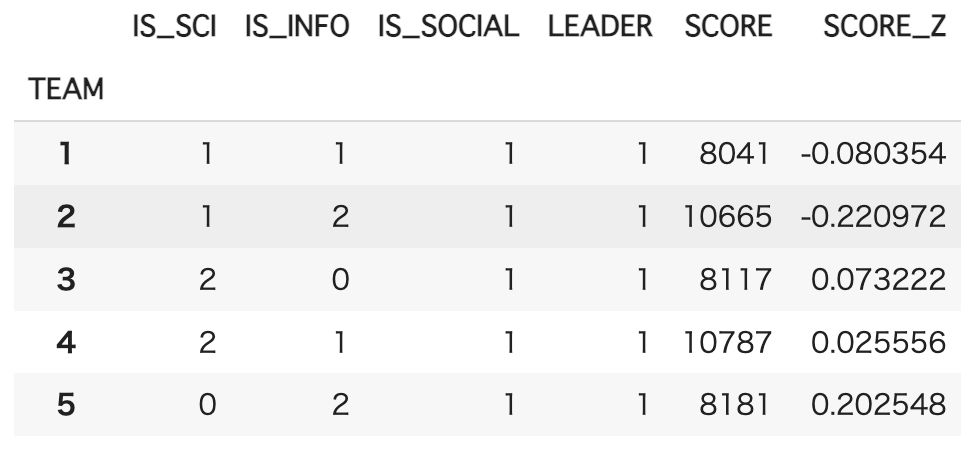
得られた解のチームごとに各専攻とリーダーの人数、スコアの合計値を集計した表を以下に示します。表より、各チームにリーダーが1人以上いて、専攻もバランスよく割り当てられていることが見て取れます。ただ、4人チームは3人チームと比べてスコアの合計値は高くなってしまいましたが、スコアの値のスケールも大きいため仕方ないと思っています。
 |
おわりに
同期と話しながら身近な課題を数理最適化で解決できて楽しかったです。
最後まで読んでくださり、ありがとうございました。
参考