最小二乗法の情報は、ネット上に溢れに溢れているのですが、
コーディングに至るまで複数のページを参照していたので、それらをまとめてみます。
(正直、最小二乗法そのものの理解は微妙なところです…)
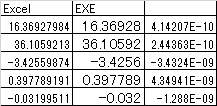
とりあえず、ゴールはEXCELのLINESTと一致するところです。
最小二乗法は近似式との差の二乗の総和が最小になる近似式を求めます。
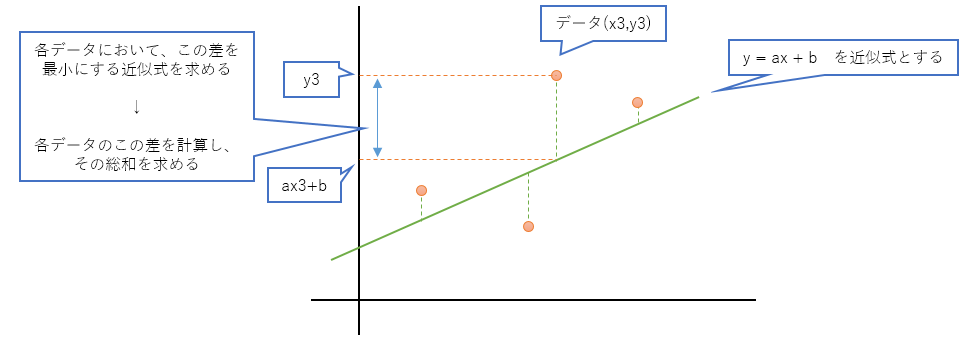
この時、近似式は、直線でも曲線でも何でもいいです。
どんな近似式においても、差は
y_i - f\left(x_i\right)
になるかなと。なので、直線式の場合は
y_i - \left(ax_i + b\right)
と。上記4点において
y_1 - \left(ax_1 + b\right)
y_2 - \left(ax_2 + b\right)
y_3 - \left(ax_3 + b\right)
y_4 - \left(ax_4 + b\right)
となります。
最小二乗法は近似式との差の二乗の総和が最小になる近似式を求めるので、
まずは、近似式との差の二乗の総和を求めます。
\left(y_1 - \left(ax_1 + b\right)+
y_2 - \left(ax_2 + b\right)+
y_3 - \left(ax_3 + b\right)+
y_4 - \left(ax_4 + b\right)\right)^2
データ数は4つとは限らないので、一般式で表します。
\sum_{i=1}^N\left(y_i - \left(ax_i + b\right)\right)^2
ここで、頑張って未知数a,bを求めていきたいのですが、
そのためには、この数式を
AX=B
の行列式にもっていく必要があります。(LU分解を用いて、プログラムで方程式を解くため)
求めたい係数の行列Xは単純に
X=\left(\begin{matrix}a\newline b\end{matrix}\right)
なのですが、この行列A、Bが結構曲者でして、どういう風に算出すればいいのかわかりませんでした。
そこで、コピペ参考にしたサイトはこちらで、かなり詳細に書いてあります。
(結論までの説明がかなり丁寧に、数式を交えて説明されています)
なので、詳細はリンク先参照ということで、結論だけ書きますと
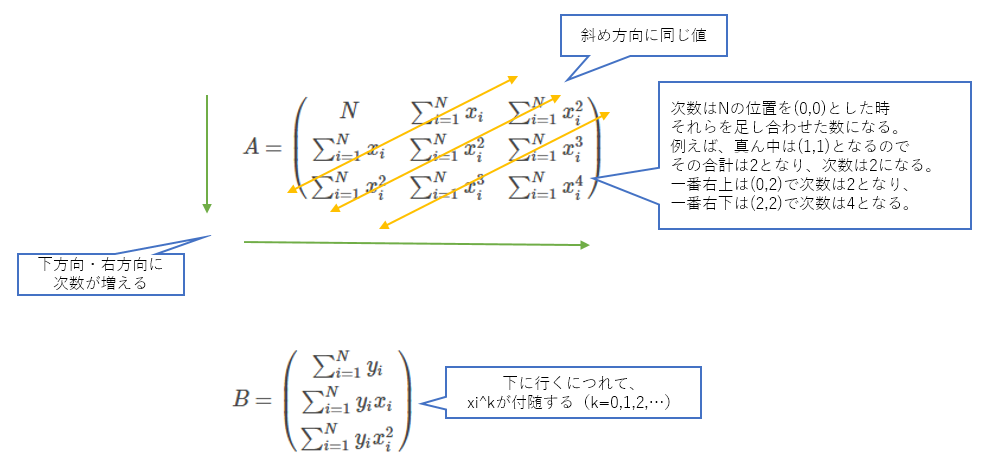
A = \left(\begin{matrix}N&\sum_{i=1}^Nx_i\newline
\sum_{i=1}^Nx_i&\sum_{i=1}^Nx_i^2\newline
\end{matrix}\right)
B=\left(\begin{matrix}\sum_{i=1}^Ny_i\newline \sum_{i=1}^Ny_ix_i\newline \end{matrix}\right)
となります。ちなみに、近似式が2次式の場合は、
\begin{array}\newline
A = \left(\begin{matrix}N&\sum_{i=1}^Nx_i&\sum_{i=1}^Nx_i^2\newline
\sum_{i=1}^Nx_i&\sum_{i=1}^Nx_i^2&\sum_{i=1}^Nx_i^3\newline
\sum_{i=1}^Nx_i^2&\sum_{i=1}^Nx_i^3&\sum_{i=1}^Nx_i^4\newline
\end{matrix}\right)
\newline\end{array}
B=\left(\begin{matrix}\sum_{i=1}^Ny_i\newline \sum_{i=1}^Ny_ix_i\newline \sum_{i=1}^Ny_ix_i^2\newline \end{matrix}\right)
となり、行列A、Bにおいて下記法則性が見えるので問題ないかと思います。
私の場合は、近似式が4次式だったので、
\begin{array}\newline
AX = B \newline
\left(\begin{matrix}N&\sum_{i=1}^Nx_i&\sum_{i=1}^Nx_i^2&\sum_{i=1}^Nx_i^3&\sum_{i=1}^Nx_i^4\newline
\sum_{i=1}^Nx_i&\sum_{i=1}^Nx_i^2&\sum_{i=1}^Nx_i^3&\sum_{i=1}^Nx_i^4&\sum_{i=1}^Nx_i^5\newline
\sum_{i=1}^Nx_i^2&\sum_{i=1}^Nx_i^3&\sum_{i=1}^Nx_i^4&\sum_{i=1}^Nx_i^5&\sum_{i=1}^Nx_i^6\newline
\sum_{i=1}^Nx_i^3&\sum_{i=1}^Nx_i^4&\sum_{i=1}^Nx_i^5&\sum_{i=1}^Nx_i^6&\sum_{i=1}^Nx_i^7\newline
\sum_{i=1}^Nx_i^4&\sum_{i=1}^Nx_i^5&\sum_{i=1}^Nx_i^6&\sum_{i=1}^Nx_i^7&\sum_{i=1}^Nx_i^8\newline
\end{matrix}\right)
\left(\begin{matrix}
a_0\newline
a_1\newline
a_2\newline
a_3\newline
a_4\newline
\end{matrix}\right)
=
\left(\begin{matrix}
\sum_{i=1}^Ny_i\newline
\sum_{i=1}^Ny_ix_i\newline
\sum_{i=1}^Ny_ix_i^2\newline
\sum_{i=1}^Ny_ix_i^3\newline
\sum_{i=1}^Ny_ix_i^4\newline
\end{matrix}\right)
\newline\end{array}
とまぁ、こんな感じです。
コードにするとこんな感じ。
//gainとpressがそれぞれ取得データ(List<double>)
//あらかじめ用意しておく Loopは独自拡張メソッド(ただの繰り返し処理なので、forで置き換えても同じ)
//今回はnum=5
List<double> A_press = (num * 2 - 1).Loop(i => gain.Select_ToList(a => Math.Pow(a, i)).Sum());
//A行列の場合、i+jがそのまま次数となるためそれを利用
List<List<double>> A = num.Loop(i => num.Loop(j => A_press[i + j]));
List<double> B = num.Loop(i => press.Zip(gain, (p, g) => p * Math.Pow(g, i)).Sum());
下準備が完了したところで、ここから方程式を解くために行列AをLU分解します。
LU分解のコピペ参考元はこちらになります。
まず、行列L、Uは下記のように定義されます。
\begin{array}\newline
A=LU \newline
L = \left(\begin{matrix}1&0&0&0&0\newline
b_{21}&1&0&0&0\newline
b_{31}&b_{32}&1&0&0\newline
b_{41}&b_{42}&b_{43}&1&0\newline
b_{51}&b_{52}&b_{53}&b_{54}&1\newline
\end{matrix}\right) \newline
U = \left(\begin{matrix}
c_{11}&c_{12}&c_{13}&c_{14}&c_{15}\newline
0&c_{22}&c_{23}&c_{24}&c_{25}\newline
0&0&c_{33}&c_{34}&c_{35}\newline
0&0&0&c_{44}&c_{45}\newline
0&0&0&0&c_{55}\newline
\end{matrix}\right) \newline
\newline\end{array}
つまり
\left(\begin{matrix}N&\sum_{i=1}^Nx_i&\sum_{i=1}^Nx_i^2&\sum_{i=1}^Nx_i^3&\sum_{i=1}^Nx_i^4\newline
\sum_{i=1}^Nx_i&\sum_{i=1}^Nx_i^2&\sum_{i=1}^Nx_i^3&\sum_{i=1}^Nx_i^4&\sum_{i=1}^Nx_i^5\newline
\sum_{i=1}^Nx_i^2&\sum_{i=1}^Nx_i^3&\sum_{i=1}^Nx_i^4&\sum_{i=1}^Nx_i^5&\sum_{i=1}^Nx_i^6\newline
\sum_{i=1}^Nx_i^3&\sum_{i=1}^Nx_i^4&\sum_{i=1}^Nx_i^5&\sum_{i=1}^Nx_i^6&\sum_{i=1}^Nx_i^7\newline
\sum_{i=1}^Nx_i^4&\sum_{i=1}^Nx_i^5&\sum_{i=1}^Nx_i^6&\sum_{i=1}^Nx_i^7&\sum_{i=1}^Nx_i^8\newline
\end{matrix}\right)
=
\left(\begin{matrix}1&0&0&0&0\newline
b_{21}&1&0&0&0\newline
b_{31}&b_{32}&1&0&0\newline
b_{41}&b_{42}&b_{43}&1&0\newline
b_{51}&b_{52}&b_{53}&b_{54}&1\newline
\end{matrix}\right)
\left(\begin{matrix}
c_{11}&c_{12}&c_{13}&c_{14}&c_{15}\newline
0&c_{22}&c_{23}&c_{24}&c_{25}\newline
0&0&c_{33}&c_{34}&c_{35}\newline
0&0&0&c_{44}&c_{45}\newline
0&0&0&0&c_{55}\newline
\end{matrix}\right)
となります。
これらをすべて展開すると
U[0][0] = A[0][0];
U[0][1] = A[0][1];
U[0][2] = A[0][2];
U[0][3] = A[0][3];
U[0][4] = A[0][4];
L[0][0] = 1;
L[1][0] = A[1][0] / U[0][0];
L[2][0] = A[2][0] / U[0][0];
L[3][0] = A[3][0] / U[0][0];
L[4][0] = A[4][0] / U[0][0];
U[1][0] = 0;
U[1][1] = A[1][1] - L[1][0] * U[0][1];
U[1][2] = A[1][2] - L[1][0] * U[0][2];
U[1][3] = A[1][3] - L[1][0] * U[0][3];
U[1][4] = A[1][4] - L[1][0] * U[0][4];
L[0][1] = 0;
L[1][1] = 1;
L[2][1] = (A[2][1] - L[2][0] * U[0][1]) / U[1][1];
L[3][1] = (A[3][1] - L[3][0] * U[0][1]) / U[1][1];
L[4][1] = (A[4][1] - L[4][0] * U[0][1]) / U[1][1];
U[2][0] = 0;
U[2][1] = 0;
U[2][2] = A[2][2] - L[2][0] * U[0][2] - L[2][1] * U[1][2];
U[2][3] = A[2][3] - L[2][0] * U[0][3] - L[2][1] * U[1][3];
U[2][4] = A[2][4] - L[2][0] * U[0][4] - L[2][1] * U[1][4];
L[0][2] = 0;
L[1][2] = 0;
L[2][2] = 1;
L[3][2] = (A[3][2] - L[3][0] * U[0][2] - L[3][1] * U[1][2]) / U[2][2];
L[4][2] = (A[4][2] - L[4][0] * U[0][2] - L[4][1] * U[1][2]) / U[2][2];
U[3][0] = 0;
U[3][1] = 0;
U[3][2] = 0;
U[3][3] = A[3][3] - L[3][0] * U[0][3] - L[3][1] * U[1][3] - L[3][2] * U[2][3];
U[3][4] = A[3][3] - L[3][0] * U[0][4] - L[3][1] * U[1][4] - L[3][2] * U[2][4];
L[0][3] = 0;
L[1][3] = 0;
L[2][3] = 0;
L[3][3] = 1;
L[4][3] = (A[4][3] - L[4][0] * U[0][3] - L[4][1] * U[1][3] - L[4][2] * U[2][3]) / U[3][3];
U[4][0] = 0;
U[4][1] = 0;
U[4][2] = 0;
U[4][3] = 0;
U[4][4] = A[4][4] - L[4][0] * U[0][4] - L[4][1] * U[1][4] - L[4][2] * U[2][4] - L[4][3] * U[3][4];
L[0][4] = 0;
L[1][4] = 0;
L[2][4] = 0;
L[3][4] = 0;
L[4][4] = 1;
となるはず。(力技)
これをコードで表現すると
for (int i = 0; i < A.Count; i++)
{
for (int j = 0; j < num; j++)
{
double sigmaU = i.Loop(k => L[i][k] * U[k][j]).Sum();
U[i][j] = (i <= j) ? A[i][j] - sigmaU
: 0;
double sigmaL = j.Loop(k => L[i][k] * U[k][j]).Sum();
L[i][j] = (i > j) ? (A[i][j] - sigmaL) / U[j][j]
: (i == j) ? 1
: 0;
}
}
ここで一度
AX=B
に戻ってみます。この式がLU分解により
LUX=B
となったので、まずは
LZ=B
として、行列Zを求めていきます。つまり、下記式ですね。
\left(\begin{matrix}1&0&0&0&0\newline
b_{21}&1&0&0&0\newline
b_{31}&b_{32}&1&0&0\newline
b_{41}&b_{42}&b_{43}&1&0\newline
b_{51}&b_{52}&b_{53}&b_{54}&1\newline
\end{matrix}\right)
\left(\begin{matrix}
z_{11}\newline
z_{21}\newline
z_{31}\newline
z_{41}\newline
z_{51}\newline
\end{matrix}\right)
=
\left(\begin{matrix}
\sum_{i=1}^Ny_i\newline
\sum_{i=1}^Ny_ix_i\newline
\sum_{i=1}^Ny_ix_i^2\newline
\sum_{i=1}^Ny_ix_i^3\newline
\sum_{i=1}^Ny_ix_i^4\newline
\end{matrix}\right)
これらを分解すると
\begin{array}\newline
\left(\begin{matrix}
z_1 \newline
b_{21}z_1 + z_2 \newline
b_{31}z_1 + b_{32}z_2 + z_3 \newline
b_{41}z_1 + b_{42}z_2 + b_{43}z_3 + z_4 \newline
b_{51}z_1 + b_{52}z_2 + b_{53}z_3 + b_{54}z_4 + z_5 \newline
\end{matrix}\right)
=
\left(\begin{matrix}
\sum_{i=1}^Ny_i\newline
\sum_{i=1}^Ny_ix_i\newline
\sum_{i=1}^Ny_ix_i^2\newline
\sum_{i=1}^Ny_ix_i^3\newline
\sum_{i=1}^Ny_ix_i^4\newline
\end{matrix}\right)
\newline\end{array}
となります。
ここで、未知の行列Zを求めるために式を整理します(ただ移項するだけ)
\begin{array}\newline
\left(\begin{matrix}
z_1 \newline
z_2 \newline
z_3 \newline
z_4 \newline
z_5 \newline
\end{matrix}\right)
=
\left(\begin{matrix}
\sum_{i=1}^Ny_i\newline
\sum_{i=1}^Ny_ix_i - b_{21}z_1 \newline
\sum_{i=1}^Ny_ix_i^2 - (b_{31}z_1 + b_{32}z_2)\newline
\sum_{i=1}^Ny_ix_i^3 - (b_{41}z_1 + b_{42}z_2 + b_{43}z_3)\newline
\sum_{i=1}^Ny_ix_i^4 - (b_{51}z_1 + b_{52}z_2 + b_{53}z_3 + b_{54}z_4)\newline
\end{matrix}\right)
\newline\end{array}
z1がわかっているので、それを2行目に代入して、z2を求め、その結果からさらに3行目に代入してz3を求める感じで
すべての行列Zの値を求めます。
(※行列L(bij)と行列Bは既知で、行列Zが未知)
ただ、コーディングが前提になるのでこれらを一般化します。
y_i = b_i - \sum_{k=1}^{i-1}b_{ik}z_k
コードで表現すると下記のようになります。
List<double> Z = ListUtil.CreateNewList<double>(num); //指定数の配列を作成する独自の拡張メソッド num = 5
for (int i = 0; i < num; i++)
{
double sigma_C = 0; //i=0 のときは計算されない。つまりZ[0]=B[0]
for (int k = 0; k < i; k++)
{
sigma_C += L[i][k] * Z[k];
}
Z[i] = B[i] - sigma_C;
}
ここまでこれば、あと本丸の行列Xを求めるだけ。
Z=UX
より、
\begin{array}\newline
\left(\begin{matrix}
z_1 \newline
z_2 \newline
z_3 \newline
z_4 \newline
z_5 \newline
\end{matrix}\right)
=
\left(\begin{matrix}
c_{11}&c_{12}&c_{13}&c_{14}&c_{15}\newline
0&c_{22}&c_{23}&c_{24}&c_{25}\newline
0&0&c_{33}&c_{34}&c_{35}\newline
0&0&0&c_{44}&c_{45}\newline
0&0&0&0&c_{55}\newline
\end{matrix}\right)
\left(\begin{matrix}
a_1 \newline
a_2 \newline
a_3 \newline
a_4 \newline
a_5 \newline
\end{matrix}\right)
\newline\end{array}
これらを分解すると
\begin{array}\newline
\left(\begin{matrix}
z_1 \newline
z_2 \newline
z_3 \newline
z_4 \newline
z_5 \newline
\end{matrix}\right)
=
\left(\begin{matrix}
c_{11}a_1 + c_{12}a_2 + c_{13}a_3 + c_{14}a_4 + c_{15}a_5 \newline
c_{22}a_2 + c_{23}a_3 + c_{24}a_4 + c_{25}a_5 \newline
c_{33}a_3 + c_{34}a_4 + c_{35}a_5 \newline
c_{44}a_4 + c_{45}a_5 \newline
c_{55}a_5 \newline
\end{matrix}\right)
\newline\end{array}
となります。
ここで、未知の行列Xを求めるために式を整理します(ただ移項するだけ)
\begin{array}\newline
\left(\begin{matrix}
x_1 \newline
x_2 \newline
x_3 \newline
x_4 \newline
x_5 \newline
\end{matrix}\right)
=
\left(\begin{matrix}
\frac { y_1 - (c_{11}a_1 + c_{12}a_2 + c_{13}a_3 + c_{14}a_4 + c_{15}a_5)}{c_{11}} \newline
\frac { y_2 - (c_{22}a_2 + c_{23}a_3 + c_{24}a_4 + c_{25}a_5)}{c_{22}} \newline
\frac { y_3 - (c_{33}a_3 + c_{34}a_4 + c_{35}a_5)}{c_{33}} \newline
\frac { y_4 - (c_{44}a_4 + c_{45}a_5)}{c_{44}} \newline
\frac { y_5 - c_{55}a_5}{c_{55}} \newline
\end{matrix}\right)
\newline\end{array}
同様に、すべての行列Xの値を求めます。
(※行列U(cij)と行列Zは既知で、行列Xが未知)
ただ、コーディングが前提になるのでこれらを一般化します。
x_i = \frac{ y_i - \sum_{k=i+1}^{5}c_{ik}x_k }{ c_{ii}}
コードで表現すると下記のようになります。
List<double> res = ListUtil.CreateNewList<double>(num);
for (int i = num - 1; i >= 0; i--)
{
double sigma_Res = 0;
for (int k = i; k < num; k++)
{
sigma_Res += U[i][k] * res[k];
}
res[i] = (Z[i] - sigma_Res) / U[i][i];
}
これでようやく、係数が算出できました(res配列の要素)
ソースをまとめるとこんな感じです。
//あらかじめ用意しておく
List<double> A_press = (num * 2 - 1).Loop(i => gain.Select_ToList(a => Math.Pow(a, i)).Sum());
//A行列の場合、i+jがそのまま次数となるためそれを利用
List<List<double>> A = num.Loop(i => num.Loop(j => A_press[i + j]));
List<double> B = num.Loop(i => press.Zip(gain, (p, g) => p * Math.Pow(g, i)).Sum());
List<List<double>> L = ListUtil.CreateNewList(A.Count, () => ListUtil.CreateNewList<double>(num));
List<List<double>> U = ListUtil.CreateNewList(A.Count, () => ListUtil.CreateNewList<double>(num));
for (int i = 0; i < A.Count; i++)
{
for (int j = 0; j < num; j++)
{
double sigmaU = i.Loop(k => L[i][k] * U[k][j]).Sum();
U[i][j] = (i <= j) ? A[i][j] - sigmaU
: 0;
double sigmaL = j.Loop(k => L[i][k] * U[k][j]).Sum();
L[i][j] = (i > j) ? (A[i][j] - sigmaL) / U[j][j]
: (i == j) ? 1
: 0;
}
}
//上記で、行列AをL行列、U行列に分解
//下記で、Ax=B⇒LUx=B⇒Ly=Bからyを求める
//c行列の計算
List<double> Z = ListUtil.CreateNewList<double>(num); //指定数の配列を作成する独自の拡張メソッド
for (int i = 0; i < num; i++)
{
double sigma_C = 0;
for (int k = 0; k < i; k++)
{
sigma_C += L[i][k] * Z[k];
}
Z[i] = B[i] - sigma_C;
}
//最後にy(既知)=Uxを計算しxをはじき出す
//出力行列の計算
List<double> res = ListUtil.CreateNewList<double>(num);
for (int i = num - 1; i >= 0; i--)
{
double sigma_Res = 0;
for (int k = i; k < num; k++)
{
sigma_Res += U[i][k] * res[k];
}
res[i] = (Z[i] - sigma_Res) / U[i][i];
}
まぁ今更ですけど、車輪の再発明とか言わないで…。
(どっかに落ちてるライブラリを用いる方が、いろいろとよろしいかと…)
最後に改めてコピペ参考元を。
http://qiita.com/nakataSyunsuke/items/15a761506a401d108cad
http://hooktail.org/computer/index.php?LU%CA%AC%B2%F2