これまで、『プログラマ脳を鍛える数学パズル』『もっとプログラマ脳を鍛える数学パズル』という本を書いてきました。
そして、この度『プログラマを育てる脳トレパズル』という本を書きました。
これまでの2冊は主にRubyやJavaScriptで解説していましたが、今回の本ではPythonで解説しています。
これらのパズル問題の多くは、主にCodeIQというサービスで出題していたものです。
当時出題していた問題の中に、まだ書籍に掲載していない問題がいくつかあるのですが、今回の書籍の読者層を考えたとき、少し数学的な要素が強かったり、難易度の面でレベルが合わず、最終的に掲載を断念した問題をここでPythonのソースコードと合わせて紹介しておきます。
ぜひ解答例のソースコードを見ずに、自分で実装してみてください。
Q1. たくさん組み合わせて作る合成抵抗
問題
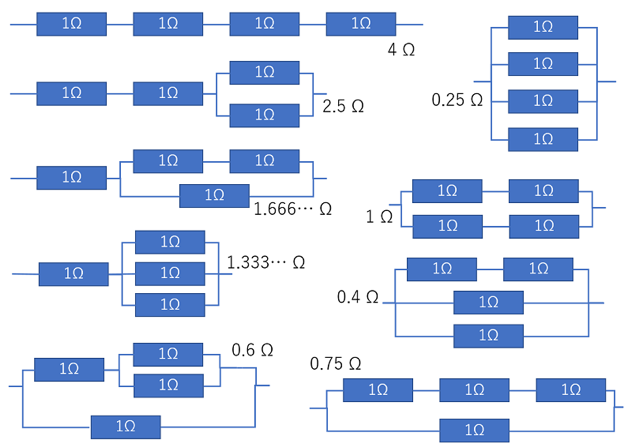
すべて1オーム[Ω]の抵抗を直列または並列に組み合わせて、合成抵抗を作ることを考えます。
このとき、違う配置でも同じ値になれば1つとしてカウントします。
なお、合成抵抗の計算は、以下のようになります。
- 直列に $m$ 個の抵抗を並べたとき
R=R_1+R_2+⋯+R_m
- 並列に $m$ 個の抵抗を並べたとき
\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\cdots+\frac{1}{R_m}
例えば、3つの抵抗を並べると、その合成抵抗の値は次のようになります。
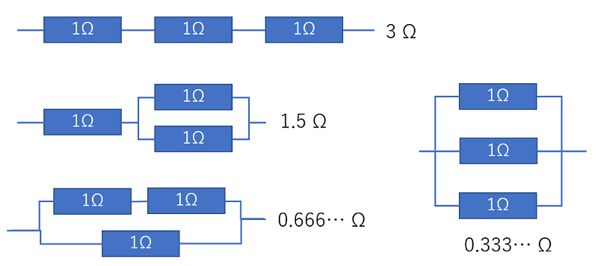
12個の抵抗を並べたときにできる、合成抵抗の値が何通りあるかを求めてください。
なお、上記のような単純な直列と並列だけを考え、複雑な合成抵抗は考えないものとします。
考え方
3つ以上が並列に並ぶパターンは、2つの抵抗を並列に並べ、さらに残りを順に並列に並べたものと考えられます。
【STEP 1】
違う配置でも同じ値になれば1つとしてカウントするため、合成抵抗の値のみリストアップします。また、リスト(配列)に格納するのではなく、Pythonのset(集合)を使うことで、重複した要素を追加しても取り除かれるようにします。
【STEP 2】
直列は左右2つに分け、それぞれについて再帰的に合成抵抗を調べたあと、その結果をまとめます。
また、並列は上下2つに分け、それぞれについて再帰的に合成抵抗を調べたあと、その結果をまとめます。
直列の場合はそれぞれの抵抗の値を足し算するだけですが、並列の場合は問題文の式を変形して考えます。
例えば、2個の場合は $\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}$ なので、これを変形すると $R=\frac{R_1\times R_2}{R_1+R_2}$ となります。
小数で計算しても問題ありませんが、より正確に計算するために、Pythonのfractionsを使うと分数のまま処理できます。
from functools import lru_cache
from fractions import Fraction
@lru_cache(maxsize=1000)
def search(n):
if n == 1:
return [1]
val = set([])
for i in range(1, n // 2 + 1): # 直列
for l in search(i):
for r in search(n - i):
val.add(l + r)
for i in range(1, n // 2 + 1): # 並列
for u in search(i):
for d in search(n - i):
val.add(Fraction(u * d, u + d))
return val
n = 12
print(len(search(n)))
解答
14,517通り
Q2. 目盛りの消えた円
問題
有名なパズル問題の一つに「Spacer Ruler」があります。
「目盛りの消えたものさし」とも言われ、できるだけ少ない目盛りの数で1cm単位の整数を測ります。
例えば、1cm刻みで目盛りが付いている長さ10cmのものさしの場合、左図の下側にある4つの目盛りが残っていると、それを組み合わせて図のように1cm~10cmまで測ることが可能です。
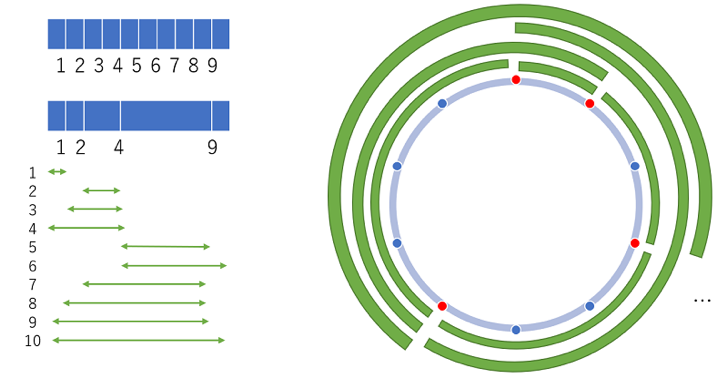
これを右図のように円形で考えてみます。円周を10個に分割した目盛りのうち、できるだけ多くの目盛りを消して1~10までを測ります。
例えば、右図の赤色の4点だけ残すと1~10までを測れます。3点だけ残して、1~10までを測ることはできませんので、少なくとも4点が必要です。
円周を30個に分割した目盛りのうち、できるだけ多くの目盛りを消して1〜30までを測るとき、残った目盛りの数が最も少なくなる場合の目盛りの個数を求めてください。
考え方
1周すれば30は測れますので、1〜29までを測る目盛りの位置を探します。また、円周のどこからはじめても結果は同じなので、ここでは一番上の部分からスタートする目盛りの配置を数えると十分です。
目盛りの数を少ない方から順に試して、1〜30までのすべての長さを測定できるものがあれば探索を終了できます。
目盛りの位置を重複しない組み合わせのリストで生成するには、Pythonであればitertoolsモジュールにあるcombinationsを使うと簡単です。
【STEP 1】
簡単にするため、円を6個に分割して、そのうち3箇所を使って1〜6までの長さを測定することを考えましょう。円の一番上を0とすると、全部で「0, 1, 2, 3, 4, 5」と番号をつけられます。ここから3つを選んでみます。
「0」は固定できるので、1〜5から2つを選ぶ組み合わせを考えると、「1, 2」「1, 3」「1, 4」「1, 5」「2, 3」「2, 4」「2, 5」「3, 4」「3, 5」「4, 5」の10通りが考えられます。これを生成するには、次のように書きます。これで、[1, 2, 3, 4, 5]というリストから2つ選ぶ組み合わせを生成できます。
import itertools
itertools.combinations([i for i in range(1, 6)], 2)
このitertools.combinationsではタプルが生成されます。タプルはリストと同じように複数の要素を格納できますが、リストとは異なり要素の追加や変更はできません。
【STEP 2】
生成した組み合わせの先頭に「0」を追加すると目盛りの配置が決まります。
この配置から1つずつ取り出し、残りの目盛りとの距離を計算します。
これをPythonのset(集合)に追加していくことで、重複することなく距離の一覧を生成できます(このとき、円なので逆方向も調べる)。
すべての目盛りをチェックしたとき、1〜30まで計測できれば完了です。
import itertools
n = 30
c = 1
while True:
for i in itertools.combinations([i for i in range(1, n)], c):
ans = set([])
for s in [0] + list(i):
for e in [j for j in list(i) + [n] if j > s]:
ans.add(e - s) # 右まわりの距離
if n != e - s:
ans.add(n - (e - s)) # 左まわりの距離
if len(ans) == n: # すべて計測できれば完了
print(c + 1)
exit()
c += 1
解答
7個(頂点を0とすると、例えば「0, 1, 2, 3, 4, 9, 19」の位置がある)
Q3. 数字が最大のマインスイーパ
問題
Windowsに標準で搭載されていたゲームとして有名なマインスイーパ。
長方形のマスの中に地雷が埋まっており、その隣接するマスに書かれている数字を元に、地雷の場所を特定します。
このとき、隣接するというのは、上下左右だけでなく、斜めの位置も含みます。
なお、地雷があるマスに数字が書かれることはありません。
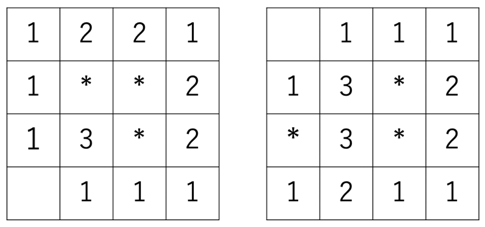
例えば、4×4のマスの中に3つの地雷が埋まっているとき、次のようなさまざまな配置が考えられます。
ここで、左のように地雷を配置すると数字の和は18ですが、右のように配置すると19となり、このとき最大となります。
5×6のマスの中に5個の地雷が埋まっているとき、マスの中に書かれている数字の和の最大値を求めてください。
考え方
まずは地雷をどこに配置するか考えます。
左上から順に、地雷を配置するかしないか、右下まで繰り返し、5個の地雷を配置するパターンを調べます。
調べ終わったら、それぞれの配置について、地雷の周囲に数字を入れていきます。
このように、先に地雷を配置する場所を決めることで、数字の値は自動的に決まります。この配置の組み合わせは、30個のマスの中に5個の地雷を配置する組み合わせなので、 $_{30} C_5=\frac{30\times 29\times 28\times 27\times 26}{5\times 4\times 3\times 2\times 1}=142,506$ 通りです。
この量なら、全探索してもなんとか処理できそうです。また、データ構造を工夫すると、それなりに高速に処理できます。
地雷を配置したあとで数字を決める部分で、今回必要なのは数字の和だけであり、個々の数字は必要ありません(もちろん求めてもそれほど処理時間は変わりませんが)。
必要なのは数字の和の最大となる場合だけなので、左右を反転したものや上下を反転したものは同じ結果となります。
これをうまく工夫すると大幅な処理時間の短縮が可能です。
【STEP1】
すぐに思いつくのは、マスを2次元で表現する方法です。
例えば、地雷を配置する場所をx,yのペアで記録し、その周囲に入る数をカウントする方法が考えられます。
左上から右下に向けて、地雷を配置するかどうか考えながら深さ優先探索で配置し、すべての地雷を配置できたら、周囲の数字を合計してみます。
周囲の数字は、横方向と縦方向に、地雷の位置から±1した範囲を調べ、それがマスの範囲内ならばカウントするとよいでしょう。
w, h = 5, 6
def calc(mine): # 周囲の数字の合計を計算する
cnt = 0
for x, y in mine: # 地雷を1つずつ取り出し
for dx in [-1, 0, 1]: # 横方向の移動
for dy in [-1, 0, 1]: # 縦方向の移動
if (x + dx > 0) and (x + dx <= w) \
and (y + dy > 0) and (y + dy <= h):
# マスの範囲内のとき
if [x + dx, y + dy] not in mine:
# その場所に地雷がなければカウント
cnt += 1
return cnt
def make(x, y, remain, mine):
if remain == 0: # すべて配置できたとき
return calc(mine)
if x > w: # 横方向を超えたら次の行に
return make(1, y + 1, remain, mine)
elif y > h: # 最後の行でも地雷を配置できなかったら失敗
return 0
else:
# 地雷を置くときと置かないときの大きい方を返す
return max([
make(x + 1, y, remain, mine),
make(x + 1, y, remain - 1, mine + [[x, y]])
])
print(make(1, 1, 5, []))
【STEP2】
上記でも数秒で処理できますし、データ構造としてビット演算を使うともう少し判定が簡単になり、処理速度を数倍にできます。
ここでは、もっと高速化する方法として、無駄な探索を省いてみましょう。
「考え方」にも書いたように、左右の反転や上下の反転は探索する必要がありません。
このような対称性を考え、次の図のような4つの部分に分けて考えてみましょう。
このように配置すると、Dに配置する地雷の数が0というのは考える必要がありません。
そこで、Dとそれ以外に分けて探索します(A, B, C, Dのどれでも構いませんが、Dを使うのが実装上楽になります)。
このように、対称形の場合は、分割して考えることで探索するサイズを小さくできます。
# 略(上記のcalc関数までは同じ)
def check_area(x, y, turn):
# Dの領域
min_x, max_x = w // 2 + 1, w
min_y, max_y = h // 2 + 1, h
if (x >= min_x) and (x <= max_x)\
and (y >= min_y) and (y <= max_y):
return turn >= 0
elif (x > w) or (y > h):
return False
else:
return turn < 0
def make(x, y, remain, turn, mine):
if remain == 0: # すべて配置できたとき
if turn >= 0: # D以外の場所を探す
return make(1, 1, turn, -1, mine)
else:
return calc(mine)
if y > h: # 最後の行でも地雷を配置できなかったら失敗
return 0
elif not check_area(x, y, turn): # 範囲外は次の行に
return make(1, y + 1, remain, turn, mine)
else:
# 地雷を置くときと置かないときの大きい方を返す
return max([
make(x + 1, y, remain, turn, mine),
make(x + 1, y, remain - 1, turn, mine + [[x, y]])
])
n = 5
sum = []
for i in range(1, n + 1):
sum.append(make(w // 2 + 1, h // 2 + 1, i, n - i, []))
print(max(sum))
解答
38
その他の問題
その他、多くの問題を『プログラマを育てる脳トレパズル』で紹介していますので、合わせてお読みください。