フィボナッチ数列について考えていたら、夜を明かしてしまったのでそのメモ。
寝ぼけ眼で支離滅裂な文章を書いてしまったので、これのちゃんとしたまとめ $+α$。
(https://x.com/masu_p_sekioka/status/1717324276880290180?s=20)
のつもりで書いてたら、発見数が倍になった。
$+γ$くらいある。
(基本的に数字は全て整数。)
発見その1 「フィボナッチ数列上のある数について、それの二乗と、両隣の数の積との差は常に1になる」
フィボナッチ数列$F$
$$F_0=0,\quad F_1=1,\quad F_{n+2}=F_n+F_{n+1}$$
について、常に
$$| F_n^2 - F_{n-1} F_{n+1} |=1 \quad (n\geq1)$$
であるということ。
証明↓
$$G_n = F_n^2 - F_{n-1} F_{n+1} $$
とすると、
$$G_1 = F_1^2 - F_0 F_2 =1$$
$$G_n = F_n^2 -
(F_{n+1}-F_n) F_{n+1}$$
$$= F_n^2 + F_n F_{n+1} - F_{n+1}^2 $$
$$G_{n+1} = F_{n+1}^2-F_{n} F_{n+2} $$
$$=F_{n+1}^2-F_n (F_n+F_{n+1})$$
$$=-(F_n^2 + F_n F_{n+1} - F_{n+1}^2)$$
$$=-G_n$$
よって、
$$G_{n+1} = -G_n$$
から
$$G_1,G_2,G_3,G_4,…$$
は
$$1,-1,1,-1,…$$
となり、$|G_n|$ は常に1であることが示された。
発見その2 「発見1を使うと、より一般的なフィボナッチ数列についての性質がわかる」
『より一般的なフィボナッチ数列』とは、
すべての$n$について、
$N_{n+2}=N_n+N_{n+1}$ を満たすような数列$N$のこと。
これをとりあえず「一般ナッチ数列」と命名する。
(つまり、フィボナッチ数列は$N_0=0,N_1=1$であるような一般ナッチ数列といえる。)
(絶対名前ついてると思うけど、見つけられなかった。)
この数列$N$において、
$$| N_n^2+ N_n N_{n+1} - N_{n+1}^2 |$$
は常に一定である。
(これは先ほどと全く同じ手順で証明できる。)
これを、数列$N$に対して、
$$s(N) = | N_n^2+ N_n N_{n+1} - N_{n+1}^2 |$$
と定義することにする。
これを利用すれば、
適当な整数$x,y$がこの順で連続するような一般ナッチ数列$N$は
$$s(N) = |x^2+xy-y^2|$$
であるといえる。
発見その3 「一般ナッチ数列において、Nn > Nn+1 ≧ 0 となる箇所は最大でも一つしかない」
$N_n>N_{n+1} \geq 0 $ となる箇所は最大でも一つしかない。
$s(N)$ と数列$N$が一対一対応するか考えてた時に見つけた。
証明↓
$n=0$ において、 $N_0>N_1\geq 0$ が成り立つとする。
($n=m$ において $N'_m>N'_{m+1}\geq 0$ が成り立つような数列$N'$についても、
$N_n=N'_{n+m}$ となるようにズラすことで$n=0$で成り立つ$N$に変換することができるため、 一般性は失われない。)
まず、
$n\geq 0$ である $n$ について、
$$N_n \geq 0, \quad N_{n+1} \geq 0$$
を考える。
$n=0$ の時
$$N_n=N_0 \geq 0, \quad N_{n+1}=N_1 \geq 0$$
と成り立つ。
$n=k \quad (k>0)$ の時
$$N_{n}=N_{k} \geq 0, \quad N_{n+1} =N_{k+1} \geq 0$$
が成り立つと仮定すると、
$n=k+1$ の時
$$N_{n} = N_{k+1} \geq 0$$
$$N_{n+1} = N_{k+2} = N_{k}+N_{k+1} \geq 0$$
が成り立つため、数学的帰納法により
$$N_n \geq 0, \quad N_{n+1} \geq 0 \quad (n\geq 0)$$
であることが示せる。
すなわち、
$$N_{n+2}-N_{n+1}=N_n \geq 0 \quad (n \geq 0)$$
$$\Rightarrow N_{n} \leq N_{n+1} \quad (n \geq 1)$$
より、$n > 0$ では $N_n>N_{n+1}\geq 0$ が成り立たないことが示せる。
次に、
$n \leq 0$ である $n$ について、
$$N_{n} > 0, \quad N_{n-1}<0$$
を考える。
$n=0 $ の時
$$N_{n}=N_0 > 0$$
$$N_{n-1}=N_{-1}=N_{1}-N_0<0$$
と成り立つ。
$n=-2k \quad (k>0) $ の時
$$N_{n} = N_{-2k} > 0 $$
$$N_{n-1} = N_{-2k-1} < 0$$
が成り立つと仮定すると、
$n=-2(k+1)$ の時
$$N_{n}=N_{-2k-2}=N_{-2k}-N_{-2k-1} > 0$$
$$N_{n-1}=N_{-2k-3}=N_{-2k-1}-N_{-2k-2} < 0$$
が成り立つため、数学的帰納法により、
$n=-2k \quad (k \geq 0)$ では常に
$N_{n}> 0 , N_{n-1}< 0$ が成り立つことが示せた。
つまり、
$$N_{-2k}> 0 ,\quad N_{-2k-1}< 0 \quad (k \geq 0)$$
となり、正負を交互に繰り返す。
$N_{-2k-1}< 0$ より、$n < 0$ では $N_n>N_{n+1}\geq 0$ が成り立たないことが示せた。
これらのことから
$N_0>N_1\geq 0$ が成り立つと
$n≠0$ では $N_n>N_{n+1}\geq 0$ は成り立たない、
つまり
$N_n>N_{n+1}\geq 0$ が成り立つ箇所が一箇所でもあると
他に成り立つ箇所は存在しないことが示せた。
発見その4「一般ナッチ数列には3パターンしかない」
以降、$N_n>N_{n+1} \geq 0$ となるような箇所 $(N_n,N_{n+1})$ を「正の逆転対」と呼び、
$N_n<N_{n+1} \leq 0$ となる箇所 $(N_n,N_{n+1})$ を「負の逆転対」と呼ぶことにする。
(つまり発見3は、どんな一般ナッチ数列にも正の逆転対は最大で1つしかない、と言い換えることができる。)
一般ナッチ数列には、
- 正の逆転対を1つだけ持つ(負の逆転対は持たない)
正負繰り返し→正の逆転対→単調増加 - 全ての要素が$0$
- 負の逆転対を1つだけ持つ(正の逆転対は持たない)
正負繰り返し→負の逆転対→単調減少
の3パターンしかない。
1を「正ナッチ数列」、2を「ゼロ数列」、3を負ナッシ…「負ナッチ数列」と命名する。
この3パターンしかないことを示す。
↓証明
発見3の証明で、正の逆転対がある場合、負の逆転対は存在しないことも示せている。
また、負の逆転対が最大でも1つしかないことは、発見3の証明において、全ての要素を-1倍したものを考えると示せる。
同様に、負の逆転対があれば正の逆転対はないことも示せている。
よってあとは、「正の逆転対も負の逆転対も持たず、ゼロ数列でもない」という一般ナッチ数列が存在しないことを示せれば良い。
証明↓
「正の逆転対も負の逆転対も持たず、ゼロ数列でもない」ような一般ナッチ数列$N$を仮定する。
この数列に$0$が含まれる場合
$0$の直前の要素を$x$とし
- $x=0$の場合:$0$が連続しているためゼロ数列になり矛盾。
- $x>0$の場合:$x>0\geq 0$より正の逆転対を持ち矛盾。
- $x<0$の場合:$x<0\leq 0$より負の逆転対を持ち矛盾。
よって全て矛盾するため、$N$には$0$が含まれないことがわかる。
次に、$N_0,N_1$ について考える。($N_0,N_1$であることに意味はない、任意の連続する部分であれば良い。)
$N_0$と$N_1$が同符号の場合
- $N_0=N_1$の場合:$N_{-1}=N_1-N_0=0$となり矛盾。
- $N_0>N_1>0$の場合:正の逆転対$(N_0,N_1)$を持ち矛盾。
- $N_0<N_1<0$の場合:負の逆転対$(N_0,N_1)$を持ち矛盾。
- $0<N_0<N_1$の場合:
$N_{-1}=N_1-N_0>0$
もし $N_{-1}\geq N_0$ であれば $N_{-1}>N_0>0$ か $N_{-1}=N_0$ となり、これはすでに矛盾を示したため、
$0<N_{-1}<N_0$
同様の操作を行うと、
$0<N_{-k}<…<N_{-2}<N_{-1}<N_0$
$⇒0<N_{-k} \leq N_0 -k \quad (∵全ての要素は整数)$
であることが言えるが、
$k=N_1$ のとき、
$0<N_{-N_1}\leq N_1-N_1 =0$ となり矛盾する。 - $0>N_0>N_1$が矛盾することもこれと同じ手順で説明できる。
よって、$N_0$と$N_1$が同符号なら矛盾する。
つまり、$N_0$と$N_1$は異符号なはずである。
$N_0$と$N_1$が異符号の場合
-
$|N_0|=|N_1|$の場合:
異符号なので、$N_2=N_0+N_1=0$となり矛盾。 -
$|N_0|<|N_1|$の場合:
- $N_0<0<N_1$の場合:
$|N_0|=-N_0<|N_1|=N_1$ より
$0<N_0+N_1=N_2$
これは $N_1>0,N_2>0$ となる部分を作り、同符号はすでに矛盾を示した。 - $N_0>0>N_1$の場合:
$|N_0|=N_0<|N_1|=-N_1$ より
$0>N_0+N_1=N_2$
これは $N_1<0,N_2<0$ となる部分を作り、やはり同符号はすでに矛盾を示した。
よって、$|N_0|<|N_1|$ は矛盾。
- $N_0<0<N_1$の場合:
-
$|N_0|>|N_1|$の場合:
$|N_1| \leq |N_2|$ は矛盾を示したので、
$|N_1|>|N_2|$
他の部分も同様なので、
$|N_0|> |N_1|> |N_2|>…> |N_k|>0$
$⇒|N_0|-k \geq |N_k|>0 \quad (∵全ての要素は整数)$
であることが言えるが、
$k=|N_0|$ のとき、
$|N_0|-|N_0|=0\geq |N_{|N_0|}|> 0$ となり矛盾する。
よって、$N_0$と$N_1$が異符号でも矛盾する。
よって、どんな $N_0,N_1$ でも矛盾するため、このような$N$は存在しないことが示せた。
つまり、一般ナッチ数列は「正ナッチ数列」「ゼロ数列」「負ナッチ数列」のいずれかであることが示せた。
一般ナッチ数列の記法
ある一般ナッチ数列$N$を
[$N$の正の逆転対$(a,b)$ if $N$が正ナッチ数列
$N$ = |$(0,0)$ if $N$がゼロ数列
[$N$の負の逆転対$(a,b)$ if $N$が負ナッチ数列
と表記することとする。
(Qiitaのバグで場合分けをうまく書けなかった)
また、以降 $N=(a,b)$ は $N_0=a,N_1=b$ であるものとする。
( $N'_m=a,N'_{m+1}=b$ となるような数列$N'$ についても、$N_n=N'_{n+m}$ となるようにズラすことで、この条件を満たす$N$に変換することができる。このようにただズラしただけの数列は考えなくてよい。)
発見3,4より、(ズラした数列を考えなければ)この表記と一般ナッチ数列は一対一対応することがわかる。
(このため、イコールで結んでも特に問題は起きないが、とはいえやっていい表記なのかはわからん。)
$$N=(a,b),M=(-a,-b)$$
とすると、
$$N_n = -M_n$$
であることはわかる。
(帰納法で証明するだけなので略)
また、
$$s(M)=|(-a)^2+(-a)(-b)-(-b)^2|$$
$$=|a^2+ab-b^2|=s(N)$$
であることもわかる。
よって、対応する正ナッチ数列と負ナッチ数列は同じような性質を持つと考えられるため、以降は正ナッチ数列のみを考える。
ここで、正ナッチ数列は
$$a^2+ab-b^2>0 \quad (\because a>b\geq 0)$$
より、
$$s(N) = a^2+ab-b^2$$
といえる。
(簡略化のため、以降 $N=(a,b)$ のとき $s(N)=s(a,b)$ と表すこととする。)
例えば、普通のフィボナッチ数列は
$F = (1,0)$ で $s(1,0)=1$
他にも、
$N = (2,0)$ は $s(2,0)=4$
リュカ数というやつは
$N = (2,1)$ $s(2,1)=5$
と表せる。
これを用いて考えると、例えば
$s(N)=11$ となる $N$ は、$(3,1)$ と$(3,2)$ の二種類あり、$s(N)$ と $N$ は一対一対応していないことがわかった。
これでダーッと計算させたのがこちら。

$s(N)$として現れない数もあるっぽい。
ただ、$s(N)$から $(a,b)$ を見つける方法はまだわからない。
これを見ると、$(a,b)$ に対して $(a,a-b)$ も同じ$s(N)$を持つことにも気づく。
これは、
$$s(a,a-b)=a^2+a(a-b)-(a-b)^2$$
$$=a^2+ab-b^2=s(a,b)$$
と簡単に示せる。
発見その5「s(N)として現れる数の規則」
1. $s(N)$には $5n,5n±1$ のどちらかしか現れない
証明↓
$$a=5n+k,b=5m+l \quad (0\leq k,l \leq 4)$$ とすると、
$$s(a,b)=a^2+ab-b^2$$
$$≡k^2+kl-l^2 \pmod 5$$
$k=0〜4,l=0〜4$ を全て試すと、
$$s(a,b)≡0,±1 \pmod 5$$
しかありえないことがわかる。
しかし、これに当てはまっていながら$s(N)$に現れない数も存在する。
(例えば$6$は現れない。)
2. $k$と$l$が$s(N)$として現れるとすると、$kl$も$s(N)$として現れる
証明↓
$$k=s(a,b)=a^2+ab-b^2$$
$$l=s(c,d)=c^2+cd-d^2$$
とすると
$$kl=(a^2+ab-b^2)(c^2+cd-d^2)$$
$$=(ac+bd)^2+(ac+bd)(ad+bc+bd)$$
$$-(ad+bc+bd)^2$$
となり、$(ac+bd,ad+bc+bd)$を含む数列が $s(N)=kl$ となることよりわかる。
3. $s(N)$として現れる数の平方数倍は$s(N)$として現れる
証明↓
$(a,b)$ という数列全体をm倍した $(ma,mb)$ は、
$$s(ma,mb)=m^2 a^2+ma\cdot mb-m^2 b^2$$
$$=m^2 s(a,b)$$
となるため。
なので、平方数で割れるなら割れるだけ割ってしまうことにする。
つまり、約数に平方数を含まない数のみを考えれば良い。
と、残った数にとある規則が現れた。
4. $s(N)$で現れる数のうち、平方数を約数に含まない数を素因数分解すると、その素因数も $5$ か $5n±1$ になっている……!!!
(感動……!!!)
いくつか調べてみても、$s(N)$には「平方数で割り切った数の素因数が全て $5$ か $5n±1$」の数しか現れず、またこれに当てはまる数は全て現れそう。
このことを頑張って示したい。
まず、「$s(N)$のうち平方数を約数に持たない数の素因数には $5n±2$ が現れないこと」を示す。
($5n±2$ でないなら $5$ か $5n±1$ なので)
証明↓
$s(a,b)=mp$ と仮定する。$(p=5n±2,pは素数)$
ただし、$s(a,b)$ は平方数を約数に持たない。
$a,b$が$1$以外の公約数を持つ場合、$s(a,b)$は平方数で割れてしまうため、$a,b$は互いに素。
もし$a$が$p$の倍数ならば、
$$s(a,b) = a(a+b)-b^2$$
$$≡-b^2 \pmod p$$
$$mp≡0 \pmod p$$
から
$$b^2≡0 \pmod p$$
より、$b$も$p$の倍数となり、矛盾。
よって、$a$は$p$の倍数ではない。
$$4s(a,b) = 4a^2+4ab-4b^2$$
$$=5a^2-(a-2b)^2$$
$s(a,b)=mp$ から
$$4mp+(a-2b)^2=5a^2$$
より
$$5a^2≡(a-2b)^2 \pmod p$$
$5$と$p$、$a$と$p$は互いに素、$a>0$なので、
$$5a^2 \not\equiv 0 \pmod p$$
より
$$(a-2b)^2 \not\equiv 0 \pmod p$$
と言える。
よって、$(a-2b)^2$、$a^2$ そして $5a^2$ は$p$を法とするゼロでない平方剰余となる。
(平方剰余とは、$p$を法として平方数と合同になりうる数のこと。調べて初めて知った。Wikipedia平方剰余)
ルジャンドル記号を使って、
$$(\frac{a^2}{p})=1 ,\quad (\frac{5}{p})(\frac{a^2}{p})=(\frac{5a^2}{p})=1$$
より
$$(\frac{5}{p})=1$$
↓wikiより、

$$(\frac{5}{p})=1 ⇔ (\frac{p}{5})=1$$
しかし、$p≡±2\pmod 5$だから、
$$(\frac{p}{5})=-1$$
となるはずなので矛盾。
よって、平方数で割れない$s(N)$は $5n±2$ を素因数に持たない。
一旦まとめると、
- $s(N)$は$5n,5n±1$ のどちらかである
- $s(N)$として現れる数の積は、$s(N)$として現れる
- $s(N)$として現れる数の平方数倍は、$s(N)$として現れる
- $s(N)$として現れる数のうち平方数を約数に持たない数は、$5$ か $5n±1$ しか素因数に持たない
ということがわかった。
だいぶ近づきはしたが、「これらが当てはまる全ての数は$s(N)$として現れる」ということまでは示せなかった。
- $s(2,1)=5$ より、$5$ は $s(N)$として現れる
ので、
- $p≡±1 \pmod 5$ である全ての素数$p$は、$s(N)$ として現れる
ということが示せるだけでいいのだが……
発見その5.9「s(N) (mod5) の規則」
そして、途中で発見したこと。
$$s(a,b)≡(a-2b)^2 \pmod 5$$
これは
$$s(a,b)=a^2+ab-b^2$$
$$= (a-2b)^2+5(ab-b^2)$$
$$≡(a-2b)^2 \pmod 5$$
より示せる。
これ発見としては弱いかなぁ〜……$s(N)$が $5$ か $5n±1$ であることをよりスマートに示せはするけど……と、思っていたんだが
試しに $a-2b$ が同じ $s(N)$ を並べてみたら……
発見その6「⌊s(N)/5+(a-2b)²/20⌋の性質」
$$\lfloor \frac{s(a,b)}{5}+\frac{(a-2b)²}{20} \rfloor$$
が必ず「平方数」か「三角数の二倍」になる!!!
($\lfloor x \rfloor$はガウス記号、要するに切り捨て。)
↓a-2b=4の時

$a$が偶数の時、$a=2c$ とすると
$$4s(a,b)=4a^2+4ab-4b^2$$
$$=5a^2-(a-2b)^2$$
$$⇔5a^2=4s(a,b)+(a-2b)^2$$
$$⇔(\frac{a}{2})^2=\frac{s(a,b)}{5}+\frac{(a-2b)^2}{20}$$
より
$$c^2=\frac{s(a,b)}{5}+\frac{(a-2b)^2}{20}$$
から、平方数。
$a$が奇数の時、$a=2c+1$ とすると
$$4s(a,b)=5a^2-a^2+4ab-4b^2$$
$$=5(2c+1)^2-(a-2b)^2$$
$$=20c(c+1)+5-(a-2b)^2$$
$$⇔20c(c+1)=4s(a,b)+(a-2b)^2-5$$
$$⇔c(c+1)=\frac{s(a,b)}{5}+\frac{(a-2b)^2}{20}-\frac{1}{4}$$
$c(c+1)$は整数なので、
$$c(c+1) = \lfloor \frac{s(a,b)}{5} + \frac{(a-2b)^2}{20}\rfloor $$
より、三角数の二倍($c(c+1)$)。
よって、
$$\lfloor \frac{s(a,b)}{5}+\frac{(a-2b)²}{20} \rfloor$$
は必ず「平方数」か「三角数の二倍」になる。
$\frac{(a-2b)^2}{20}$ は比較的小さい数なのでこれを利用すると、完璧ではないが$s(N)$からの逆算ができる。
↓は実際に逆算するコード。
s = <逆算したいs(N)>
c = math.ceil(math.sqrt(s/5))
kisuu_if = c*(c-1) >= (s-1)/5
if kisuu_if:
c = c-1
cc = c*(c+1)
else:
cc = c**2
r = math.sqrt((cc-s/5)*20 + 5*int(kisuu_if))
if r%1 != 0:
print("失敗")
else:
a = 2*c+int(kisuu_if)
b = (a-r)/2
print(f"a:{a},b:{b}")
(プログラマーが発狂する命名してるのは気にしないで)
ざっくりいうと、$\frac{s(N)}{5}$ より大きい平方数か三角数の二倍で最も小さいものから、$a,b$ を逆算している。
計算していくと、初めて失敗するのは$100$だが、$100=10^2$ から $(1,0)$ を$10$倍した $(10,0)$ であることはすぐにわかるため、実際にこの手法で失敗しかつ非自明な初めての数は$239$(ちなみに$s(15,1)=239$)。
これは $\frac{s(N)}{5}$ より大きい$c^2,c(c+1)$の中で一番小さいものしか検証していないためであり、検証範囲を増やせば当然成功確率は上がる。
一度計算してしまえば、範囲を広げていくのは$a$の値を$1$ずつ増やしていくのに対応するため、そこまで難しくもない。
発見その6.1「発見6をアプデ」
は〜い後日の私で〜す。
あんなきしょいことせんでよかったってことに気がついた。
思い込みって怖いね。
$$\frac{4s(N) + (a-2b)^2}{5}$$
が必ず平方数になる!!!
↑これが発見6をよりスマートにしたもの。
(偶数奇数の場合分けもなし)
証明↓
$$4s(N)=4a^2+4ab-4b^2$$
$$=5a^2-(a-2b)^2$$
より
$$a^2 = \frac{4s(N) + (a-2b)^2}{5}$$
と示せる。
これにより、逆算するコードもスッキリ書ける。
(ついでに、aを調べる範囲を「補正値」として設定できるようにもした)
def s_gyakusan(s,hose):
a_min = math.ceil(math.sqrt(s*(4/5)))
for h in range(hose):
a = a_min + h
a_2b = math.sqrt(5*a**2-4*s)
if a_2b % 1 != 0:
continue
b = (a - a_2b)/2
# (a - a_2b)は必ず偶数となる
return (a,b)
return "失敗"
s_gyakusan(<逆算したいs(N)>,<補正値>)
これも、補正値が1の時に初めて失敗するのは$100$だが、非自明な最小の失敗は$239$である。
ちなみに、補正値を増やしていくと非自明な最小の失敗は、$2$で$599(24,1)$、$3$で$1259(35,1)$、$4$で$1979(44,1)$と増えていく。
この方法で失敗するのは$a-2b$が大きい場合、つまり$b$が小さい場合であるから、この時の判定法も考えたい。
$$s(N)=a^2+ab-b^2$$
より、$b$が小さいなら単純に$s(N)$以下の最大の平方数を$a^2$とすれば上手くいきそう。
実際に、この方法と先ほどの方法(補正値1)を組み合わせた時に最小の失敗は$495(21,3)$。
ただしこれは平方数$9$で割れるため、より非自明な最小は$541 (22,3)$。
この2つの判定法を考えると、さらに面白い事実が見えてきた。
発見その7「a²の範囲」
$$\frac{4}{5}s(N) \leq a^2 \leq s(N)$$
証明↓
$\frac{4}{5}s(N) \leq a^2$は
$$a^2 = \frac{4}{5}s(N) + \frac{(a-2b)^2}{5} \geq \frac{4}{5}s(N) $$
より示せ、
$a^2 \leq s(N)$は
$$s(N)=a^2+ab-b^2$$
$$=a^2+(a-b)b \geq a^2 \quad (∵a>b\geq 0)$$
より示せる。
それぞれ $a-2b=0,b=0$ の時に等号が成立する。
このことから、$a$としてありえる整数の個数は、
$$\frac{2}{\sqrt{5}}\sqrt{s(N)}\leq a \leq \sqrt{s(N)}$$
より
$$個数\le\frac{5-2\sqrt{5}}{5}\sqrt{s(N)}<\sqrt{\frac{s(N)}{89}}$$
となり、これだけでアホみたいに可能性を減らせていることがわかる。
(これは発見6.1の補正値の上限でもある)
$$\frac{4}{5} \leq \frac{a^2}{s(N)} \leq 1$$
なので、$\frac{a^2}{s(N)}$の分布を調べるとこんな感じ↓
(だいたい100万個くらいのs(N)を調べた)
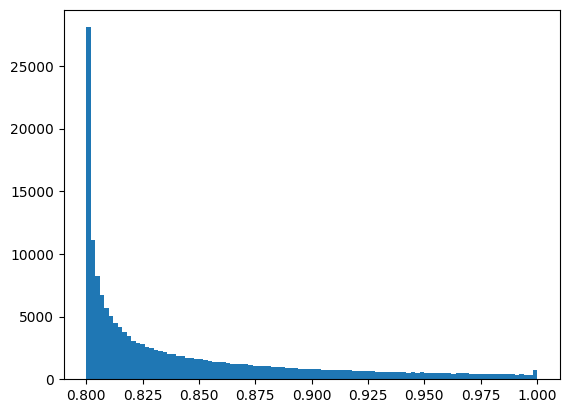
だいぶ$\frac{4}{5}$側に偏っている。
実際、この範囲内の最小の整数と$a^2$が一致するのは、調べた限りで$\frac{1}{5}$くらいあった。
$s(N)$が大きくなるに従い範囲も大きくなっていくので、こんなに一致するのはすごい。
$a$を探索するなら、$\frac{4}{5}$側からの方が効率が良さそう。
$\frac{4}{5}$側からより$1$側からの方が効率がいい可能性は、
$$(a-b)b<\frac{(a-2b)^2}{5}$$
$$⇔a^2-9ab+9b^2>0$$
$$⇔(a-\frac{9+3\sqrt{5}}{2}b)(a-\frac{9-3\sqrt{5}}{2}b)>0$$
$a\geq 2b$とすると
$$\frac{b}{a}< \frac{2}{9+3\sqrt{5}}<0.128$$
よりだいたい$\frac{1}{4}$くらいの確率っぽいことからもわかる。
結局、発見6.1の方法は思ったより優秀であることがわかった。
発見その8「一般ナッチ数列の一般項」
一般ナッチ数列の一般項は
$$N_n=\frac{1}{\sqrt{5}}[α^n(b-aβ)-β^n(b-aα)]$$
ここでついに禁止カードを発動!!!
フィボナッチ数列の一般項!!!
証明↓
こちらの記事↓よりいくつかの事実を持ってくる(ただしほんのちょっと改造)。
https://manabitimes.jp/math/643
$$α=\frac{1+\sqrt{5}}{2},β=\frac{1-\sqrt{5}}{2}$$
とおくと、
$$N_n-αN_{n-1}=β^{n-1}(N_1-αN_0)$$
$$N_n-βN_{n-1}=α^{n-1}(N_1-βN_0)$$
なので、$N_0=a,N_1=b$を代入、$N_{n-1}$を消去して、$N$の一般項は
$$N_n=\frac{1}{\sqrt{5}}[α^n(b-aβ)-β^n(b-aα)]$$
となる。
ここでさらに驚くべき事実は、
$$N_n=\frac{1}{\sqrt{5}}[α^n(b-aβ)-β^n(b-aα)]$$
$$=b・\frac{1}{\sqrt{5}}(α^n-β^n)+a・\frac{1}{\sqrt{5}}(α^{n-1}-β^{n-1})$$
$$=b・F_n+a・F_{n-1}(Fはフィボナッチ数列 )$$
となるということ!
これは面白い!
$s(N)$についても、
$$(N_n-αN_{n-1})(N_n-βN_{n-1})$$
$$=N_n^2-(α+β)N_n N_{n-1}+αβN_{n-1}^2$$
$$=N_n^2-N_n N_{n-1}-N_{n-1}^2$$
$$=(αβ)^{n-1}(N_1-αN_0)(N_1-βN_0)$$
$$=(-1)^{n-1}(b^2-ab-a^2)$$
が示せる!
……本当はこっから$s(N)$に繋げたいんだけど……
何も思いつかん……いい案あったらください……
発見終わり
ということで、私の発見はこのくらい。
結局ふわっとした結論ではあったし、この発見は絶対なんの役にも立たないと思うけど
面白いよね、こういうの。
あんまり数学にのめり込みすぎると、たかだか100年くらい軽く吹き飛ぶので割と抑えてますが、久しぶりに数学夜更かししてしまった。
私の検索力が足りないだけで、おそらく先駆者はごまんといるとは思うので、似たような話あれば教えてください。
発見おしまい。