超離散化について

超離散化について紹介します。

事前知識

• 微分方程式
• 離散化

超離散化とは

ざっくり言えば、すごい離散化ですw
丁寧に言えば、従属変数の離散化です。

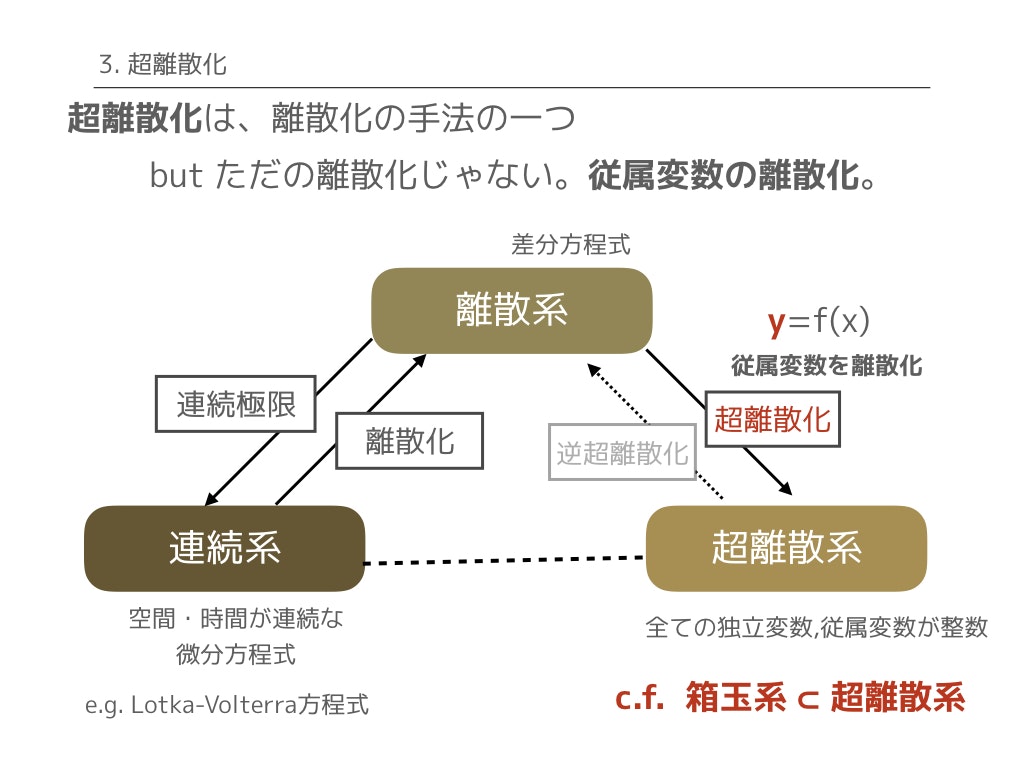
離散化(差分化)は、独立変数の離散化でしたが、超離散化ではさらに従属変数をも離散化してしまいます。つまり、全ての変数を離散化してしまうわけです。
表にしてみるとこうなります。

	連続系	離散系	超離散系
独立変数	連続	離散(一部連続)	離散
従属変数	連続	連続	離散

超離散化で用いる公式

超離散極限ってやつです。

$\displaystyle\lim_{\varepsilon\to+0}\log(e^{A/\varepsilon}+e^{B/\varepsilon}) = \max(A, B)$

こんな式が成り立ちます。証明はしないですが、実際に見てみましょう。
$A = x, B = 0$として、$\varepsilon$を0に近づけてみます。

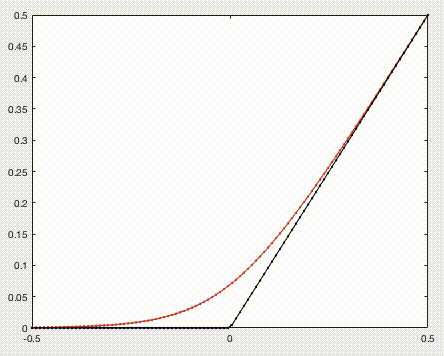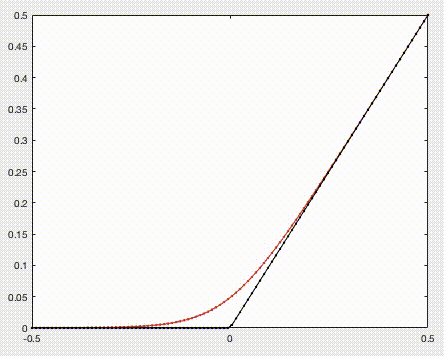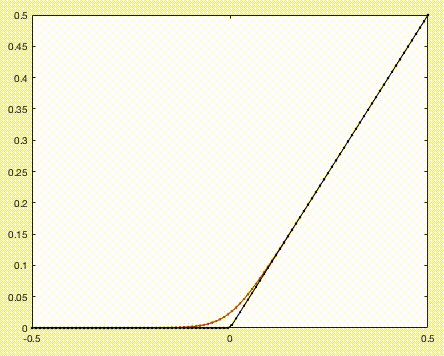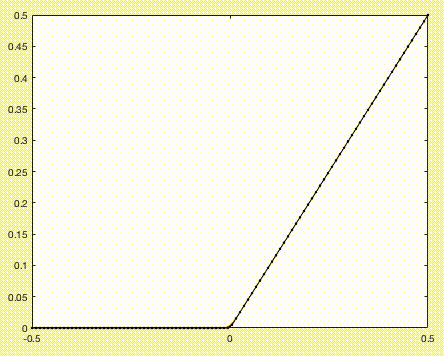
赤い線が $f(x) = \varepsilon\log(e^{x/\varepsilon}+1)$
黒い線が $g(x) = max(x, 0)$ を表しています。
赤い線が黒い線に近づいていくのが見て取れます。

超離散化

これで超離散化ができました。

何が嬉しいのか

全ての変数を離散化することにどのような利点があるのでしょうか。

まず、超離散化がどのような微分方程式に適用可能かに目を向ける必要があります。ここでは、一般的に差分化の方法が知られている、可積分系(つまり解を求められる微分方程式)を対象としています。

例えば、コンピュータでシミュレーションを行うことを考えます。可積分系を数値的にシミュレーションすると、その可積分性を表す性質はほとんど保たれていません。それらを超離散化することによって、ある程度忠実に(性質を残したまま)離散化することができるのです。また、離散化されているので、コンピュータで簡単にシミュレーションすることができるという利点もあります。