この記事はCCS Advent Calendar 2016の22日目の記事です。
はじめに
「前期にやった統計学の講義の記憶が消えたので復習したい。せっかくだから記事にしてみよう。」そういうノリで書きました。
この記事の流れ
この記事では以下の内容について触れようと思います。
- 推測統計学とは
- 確率とは
- 確率変数
- 確率分布
- 確率変数の和と再生性
- 大数の法則と中心極限定理
- 推測統計学再び
- 点推定と区間推定
- 仮説検定
厳密にやるつもりはないです。ていう良く分かってないです。
後で見返して思ったんですが、高校数学レベルの話が分かってないと「???」って感じになると思います。(分かってても「???」って感じになりそうですが…)
あと、参考文献の本やWebサイトの方が説明詳しくてわかりやすいのでこんな記事じゃなくてそっちを読んだ方が有益な気がします。(なんでこの記事書いた)
推測統計学とは
統計学というのは得られたデータをいい感じに分析する事を考える学問です。(早速雑の極み)
統計学には記述統計学やら推測統計学やらいろいろな種類があります。記述統計学っていうのは大雑把に言えばグラフを作ったり平均値を求めたりして得られたデータの特徴を掴みやすく、理解しやすくするというのが大きな目的となっている統計学です。相関係数を求めて2つの変量の関係性を調べたりとか、高校の頃数学で少しやった気がするあの辺は記述統計学の話です。
記述統計学はあくまで得られたデータについて述べる事が主な目的ですが、推測統計学はそれと異なり少ないデータから全体の情報を調べるというのが主な目的です。なぜそんなことを考えるかというと、例えば日本人の小学生の平均身長を調べるとしましょう。しかし、日本人の小学生全員の身長を調べるというのはとてもじゃないけど厳しい事が想像できます。このように知りたい集団全体(母集団といいます)について調べることができない場合、しょうがないので母集団の一部のデータ(標本といいます)を入手してそれについてあれこれ分析して母集団の情報を推測します。
ここで、どうやって標本から母集団を推測するの?っていう疑問が生じてくるのですが推測統計学では確率を用いて母集団についてあれこれ推測します。
そんな訳なのでまずは確率の話から。すでに眠い
確率とは
早速ですが僕の好きな音楽ゲームアプリ『アイドルマスター シンデレラガールズ スターライトステージ』(通称デレステ)の課金要素であるガチャについて考えてみましょう。僕に限定卯月をお恵み下さい。
公式ではガチャの確率は次のように公表されています。
| SSR | SR | R |
|---|---|---|
| 1.5% | 10% | 88.5% |
ところで、確率って何なんでしょうね?(哲学)
せっかくなので(?)確率の定義とかについて軽く触れておくことにします。
事象と確率
ガチャを引いたりサイコロを投げたりするとなんらかの結果が出ると思います。ガチャだったら当たりを引いただとか、サイコロなら1の目が出たとか、行う事によって出てくる結果が変わってきます。この「起こりうる事柄」を事象といいます。また、起こりうる全部の事象をまとめて全事象といいます。例えば(普通の)サイコロの場合1,2,3,4,5,6のいずれかが出るという6つの事象が考えられ、この6つの事象をまとめて全事象といいます。
また、複数の事象をまとめたものを考える事ができます。例えばサイコロで1が出る事象を1、同様に2,3,4,5,6を考えると例えば偶数の目を出すという事象$A$を考える事ができ、次のように書くことができます。
A=\left\{2,4,6\right\}
全事象はよく$\Omega$で書かれ、サイコロの場合は次のように表せます。
\Omega=\left\{1,2,3,4,5,6\right\}
次に「ある事象が起こる確率」について考えます。例えばサイコロで偶数の目が出る事象Aが起こる確率は普通のサイコロなら$\cfrac{1}{2}$になると考えられます。そして、これは次のように書きます。
P(A)=\cfrac{1}{2}
同様にデレステのガチャでSSRが出る事象を$B$とすると公表通りなら0.015(1.5%)であり、先ほどと同じように
P(B)=0.015
と書けます。
確率の公理
確率論では**「確率とはこういうものだ」といくつかルールを決めてそれの元で確率を考えていこうという事になっています。このルールのことを公理**といい、確率の公理は次の3つから成ります。
- 起こりうる任意の事象$A$に対し$0 \leq P(A) \leq 1$
- 全事象$\Omega$に対し$P(\Omega)=1$
- 排反な事象$A$と$B$に対して$P(A \cup B)=P(A)+P(B)$が成り立つ。
排反な事象というのは同時に起こらない事象の事です。例えばサイコロの1の目と2の目は同時には出ません(出ないはず)。偶数の目が出る事象と奇数の目が出る事象も排反です。
これを満たすものは全部確率であると考えるのが今どきの確率論での確率の定義らしい?(よく分かってない顔)
確率変数
確率変数とは取り扱うものがとりうる値(一般的なサイコロなら1から6)に対して確率が与えられている変数の事です。よく$X$などの大文字が用いられています。
例えばサイコロについて考えると、1が出る事象を$X=1$、2が出る事象を$X=2$、3以降も同様に当てはめる事ができ、その場合1が出るときの確率は次のように書けます。
P(X=1)=\frac{1}{6}
$X=2$や$X=3$についても同じように考えられます。なんでこんなものを用意するんですかって感じになるんですが、こういう風にしておいたほうが確率という不思議なものを数学的(?)に扱いやすくなるんだと思います(よく分かってない顔)。例えばデレステのガチャであれば「SSRが出る事象」を$X=1$,「SRが出る事象」を$X=2$,「Rが出る事象」を$X=3$とおけば$P(X=1)=0.015$といった感じで数式で表せますし、例えば2個のサイコロの出る目について確率変数$X_1,X_2$を考えると出る目の和$X_1+X_2$も確率変数として考えられます。また、サイコロを振って3以下が出る確率について考えるなら$P(X\leq3)$という風に不等式が使えたりします。多分できるだけ数式で扱いたいというのが理由でこういう事をしているんだと思います。(よく分かってない顔)
確率分布
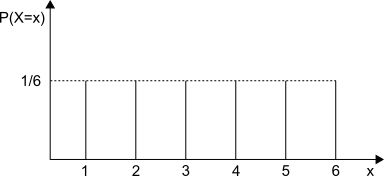
確率変数とともに登場するものとして確率分布があります。確率分布とは確率変数がとる値を$x$軸、それに対して定められている確率を$y$軸においた分布です。図を載せたほうがわかりやすそうですね。試しに(どの目も同じ確率で出る)サイコロの確率分布を見てみましょう。
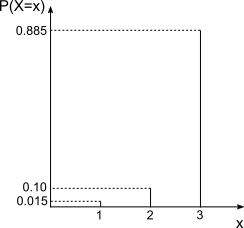
同じ確率で出るってことになってるので綺麗に並んでますね。このような分布を一様分布と言います。一様分布以外の確率分布も見てみましょう。というわけで次はデレステのガチャの確率分布です。SSRが出る事象を1、SRが出る事象を2、Rが出る事象を3として作成してみましょう。
…SSRを引くのは、大変そうですね。
一般的には要素の数が有限個である集合(多くても加算集合){$x_1,x_2,...$}のいずれかの値をとる確率変数$X$を離散型の確率変数といい、
P(X=x_k)=f(x_k) \qquad (k=1,2,...)
となる$f$を$X$の確率分布といいます。ちなみに、$f$は確率の公理を破ってはいないので(単に表記の仕方を変えているだけ?)
- $f(x_k) \geq 0 \qquad (k=1,2,...)$
- $\displaystyle\sum_{k=1}^\infty f(x_k)=1$
が成り立ちます。この$f$を「離散型の確率分布」といいます。$f$を調べればどの値が出やすいかなどがわかりそうですね。
「離散型」ってわざわざ言うあたり、何か他のタイプの確率分布があるの?って思うかもしれませんがその通りで「連続型の確率変数」があります。
一般的に確率変数$X$のとる値が関数$f(x)$によって
P(a \leq x \leq b)= \int_a^b f(x) dx
と表されるとき、$X$は連続型の確率分布をもつといいます。ただし、離散型の時と同様に
- すべての$x$に対し$\quad f(x) \geq 0$
- $\displaystyle\int_{-\infty}^\infty f(x) dx=1$
を満たすものとします。この時関数$f(x)$を$X$の「確率密度関数」といいます(離散型と少し名前が違います)。式だけ言われても
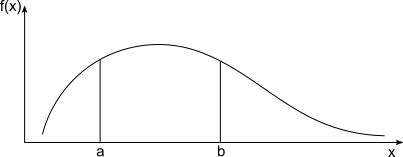
「???」って感じなので確率密度関数の図もてきとーに用意しましょう。
離散型と違い$X$のとる値が連続なので曲線になっています。また、$X$が$a$から$b$の間の値をとる確率を求める場合、離散型では$a$から$b$の範囲の中の$f(x_k)$を全て足しますが(シグマ和)、連続型の場合は$a$から$b$までで$f(x)$を積分することで求めることができます。
また、「$x$回以内にSSRを引く確率」といったようにある値以下の確率が欲しくなることがあります。なので確率変数$X$に対して
F(x)=P(X \leq x)
といったものを考えることがあります。要はある値$x$以下の確率を全部足したものを考えてみようという事です。離散型の確率分布$f(x)$と連続型の確率分布$f(x)$それぞれに対して$F(x)$を考えると次のような感じになります。
- $F(x)=\displaystyle\sum_{k=1}^x f(k) \qquad$ (離散型)
- $F(x)=\displaystyle\int_{-\infty}^x f(u)du\qquad$ (連続型)
$F(x)$を「$X$の累積分布関数」といいます。
次によく扱われるであろう期待値と分散(標準偏差)、標準化についての話をします。
期待値
期待値とは**ある試行を行ったときの結果の平均(確率の重み付き平均)**です。確率変数$X$の確率分布$f(x)$に対して期待値$E(X)$は次の式で求められます。
- $E(X)=\displaystyle\sum_x xf(x)\qquad$ (離散型)
- $E(X)=\displaystyle\int_{-\infty}^\infty xf(x)dx\qquad$ (連続型)
式だけ出されてもやはり「???」って感じなので宝くじ(離散型の確率分布)を例に挙げてみましょう。1/5の確率で500円、2/5の確率で100円もらえ、2/5の確率で外れ(何ももらえない)としましょう。この時の期待値は次の式で求められます。
500\cdot\frac{1}{5}+100\cdot\frac{2}{5}+0\cdot\frac{2}{5}=140
よって、この宝くじの期待値は「140円」です。この宝くじが100円で買えるのであれば買うべき(もらえると期待できる額のほうが多い)で、200円で買えるのであれば買わないべき(もらえると期待できる額のほうが少ない)と考えられます。(買う人は買うと思いますが)
このように、期待値はある確率を考えるときの指標の1つとして利用できますし、実際によく用いられます。
期待値について$X,Y$を確率変数、$c$を定数とすると以下の式が成り立ちます。
- $E(X+c)=E(X)+c$
- $E(cX)=cE(X)$
- $E(X+Y)=E(X)+E(Y) \qquad$ (期待値の加法性)
例えばデレステのガチャを90回(3万円弱)を引いたときのSSRの枚数の期待値を考えると、
\begin{align}
E(X) & =90\left( 1\cdot0.015+0\cdot0.985 \right) \\
& =1.35
\end{align}
となります。実際に1.35枚という枚数にはならないので、3万円費やした場合は平均して大体1枚か2枚くらいSSRが出ると考えられます。
分散と標準偏差
分散というのはある試行を行ったときの結果のばらつき具合を示すものです。分散が大きいほどばらつきが大きいといえます。確率変数$X$の期待値(重み付き平均)を$\mu$とおくと$(\mu=E(X))$、分散$V(X)$は次の式で表せます。
- $V(X)=\displaystyle\sum_x (x-\mu)^2f(x)\qquad$ (離散型)
- $V(X)=\displaystyle\int_{-\infty}^\infty (x-\mu)^2f(x)dx\qquad$ (連続型)
また、次の式で求めることもできます。
V(X)=E(X^2)-(E(X))^2
同じ平均(期待値)を満たす確率分布は無数に存在します。そこでデータのばらつき具合を示す分散を用いることでより詳しく正確に分析ができるようになります。ってなわけで平均(期待値)と同じくよく用いられます。
また、分散について$X$を確率変数、$c$を定数とすると以下の式が成り立ちます。
- $V(X+c)=V(X)$
- $V(cX)=c^2V(X)$
また、分散の平方根を標準偏差といいます。これは分散の計算過程で値を二乗しているので単位も二乗されていることから、最後にルートを付けてあげることで単位を揃えようとしたものです。
標準化
任意の確率変数$X$とそれに対する期待値$\mu(=E(X))$と分散$V(X)$を用いて
Z=\frac{X-\mu}{\sqrt{V(X)}}
とし、$Z$の期待値と分散について考えるとそれぞれの性質より
E(Z)=0, \qquad V(Z)=1
が成り立ちます。これは任意の確率変数は期待値0、分散1の確率変数に調整することが可能なことを示しています。この変換を標準化といい、$Z$を標準化変数といいます。標準化を利用すると異なる確率変数の比較を行ったりすることができるようになります。
例えば英語の成績と数学の成績を比較することを考えると、単純に英語の点数と数学の点数を比較するわけにはいきません。なぜなら平均点や分散が英語と数学で同じとは限らないからです。英語の先生が甘い試験を作り数学の先生が鬼にように難しいテストを作ったらよほど数学が得意もしくは英語が苦手ではないかぎり英語の点数の方が高いことは容易に想像できます。このような場合標準化を用いることで基準が統一でき比較ができるようになります。
ちなみによく成績で用いられる偏差値というのは平均(期待値)が50、標準偏差が10に調整された値です。例えば平均80点、標準偏差10点の試験で0点を取ると偏差値は
10\cdot\frac{0-80}{10}+50=-30
となります。…偏差値はマイナスになる事があり得ます。すごくどうでもいい気がする
以上が離散型と連続型という2種類の確率分布の基本的な性質になります。ここから先はよく用いられる(らしい)具体的な確率分布についての紹介です。
二項分布
デレステをプレイする人たち(通称プロデューサー,P)はガチャでSSR(特に自分の推しの女の子)を当てることが大きな目的となっています。なのでガチャの結果についてSSRが出る事象を成功、それ以外の事象(SRとRが出る事象)を失敗と2つのパターンに分けることができそうです。
ここで10連ガチャ(約3000円)を回す場合について考えてみましょう。この10回のガチャでSSRが$x$枚出る確率はどのくらいなのでしょうか?
SSRが出る確率は1.5%なので次の式で確率を求めることができます。
f(x)={}_{10} \mathrm{C} _x \cdot 0.015^x \cdot 0.985^{10-x} \qquad (x=0,1,...,10)
0.015(1.5%)の確率でSSRを$x$枚引き、0.985(98.5%)の確率でそれ以外を$(10-x)$枚引き、SSRが何回目のガチャで出るかの組み合わせ${}_{10} \mathrm{C}_x$の数について考え、それぞれの積を求めれば確率を得ることができます。ちなみに10連ガチャでSSRを(1枚以上)引くことができる確率は
\begin{align}
1-f(0) & =1-0.985^{10} \\
& \fallingdotseq 14\%
\end{align}
となります(全体から1枚も引けない確率を引いて求めました)。10連でSSRを引き当てるというのは思った以上に難しい感じがしますね。
Twitterなんかで10連で2枚や3枚SSRを当てているスクショを見かけたりしますが、この確率は
\begin{align}
f(2) & ={}_{10} \mathrm{C} _2 \cdot 0.015^2 \cdot 0.985^8 \\
& \fallingdotseq 0.90\% \\
f(3) & ={}_{10} \mathrm{C} _3 \cdot 0.015^3 \cdot 0.985^7 \\
& \fallingdotseq 0.0036\%
\end{align}
となっています。スゴイラッキーですね。
この例のような当たりor外れといった2通りの結果しか起きない試行(これをベルヌーイ試行といい、コイン投げなんかがよく例に挙げられます)を繰り返し行うことで得られる確率分布$f(x)$を「二項分布」といいます。
二項分布について一般的に考えてみましょう。確率$p$で成功の事象$S$、確率$(1-p)$で失敗の事象$F$が起こるベルヌーイ試行を独立に$n$回行ったときに$x$回成功$S$が起こる確率は
f(x)={}_n \mathrm{C} _x p^x(1-p)^{n-x} \qquad (x=0,1,...,n)
で表せ、この$f(x)$は離散型の確率分布の条件を満たしこの確率分布を「二項分布」と呼びます。また、$Bi(n,p)$と表されます。先ほどのガチャの場合は$Bi(10,0.015)$です。
「独立である」とは各試行が他の試行に影響を与えないという事です。ガチャでSSRを引いたからといって次に引くときSSRの確率が上がったり下がったりすることはありません。常に1.5%で変わらないです(のはず)。
確率変数$X$が二項分布$Bi(n,p)$に従っているとき期待値と分散は次のようになります。
E(X)=np, \qquad V(X)=np(1-p)
二項分布を適用できるケースは多いらしいのでこのような性質を知っておくと得かもしれない?すぐ忘れそう
ポアソン分布
次の式で表される確率分布をポアソン分布$Po(\lambda)$といいます。(唐突)
f(x)=\frac{\lambda^xe^{-\lambda}}{x!}
この確率分布に従うと考えられている現象もたくさんあるそうで、例えば交通事故の件数や製品を大量生産したときの不良品の数、遺伝子の突然変異数など「全体の数は多いけど発生確率自体は低い」ものにポアソン分布を当てはめられるそうです。(「プロシア陸軍において馬に蹴られて死んだ兵士数」なんてものもポアソン分布が当てはめられたとか)
これと関連してポアソンの少数の法則というものがあります。
$np \to \lambda$となるように$n \to \infty,p \to 0$となる極限では各$x$に対し
{}_n \mathrm{C} _x p^x(1-p)^{n-x} \to \frac{\lambda^xe^{-\lambda}}{x!}
が成り立つというのがポアソンの少数の法則(ポアソンの極限定理)というものです。ぼくはこれ成り立つ理由というか導出についてよく分かってないです(白目)
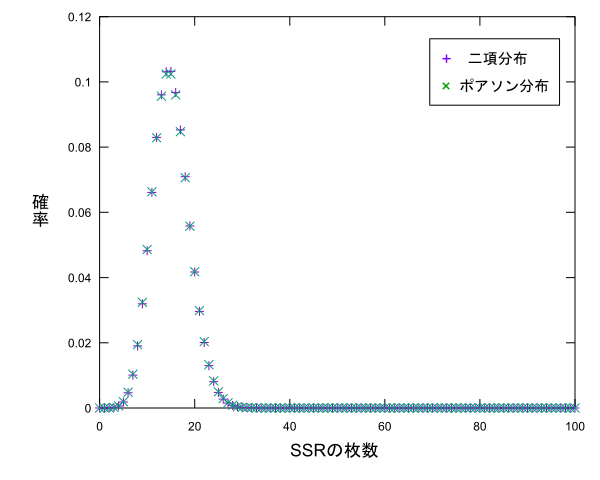
これが成り立つことから**$n$が大きく$p$が小さい二項分布$Bi(n,p)$はポアソン分布$Po(\lambda)$で近似ができる**ということが言えるみたいです。デレステのガチャを1000回回した時にSSRが$x$枚出る確率分布を示す二項分布$Bi(1000,0.015)$をポアソン分布で試しに近似して比べてみましょう。この場合は$\lambda=np=15$のポアソン分布を考えます。それぞれプロットすると次のようになります。
($x>100$はカットしました)かなり似たグラフになりましたね。というか違いが分かりません。$n$と$p$の値によりますがこのように二項分布はポアソン分布で近似できるみたいです。
「近似して一体何になるんですか?」って思うかもしれませんが$n$が大きいときの二項分布の計算は結構大変らしく、ポアソン分布を代わりに計算してもいいっていうのは結構うれしいようです。
確率変数$X$がポアソン分布に従うとき期待値と分散は
E(X)=\lambda, \qquad V(X)=\lambda
よく分からないけど両方とも$\lambda$になります。
幾何分布
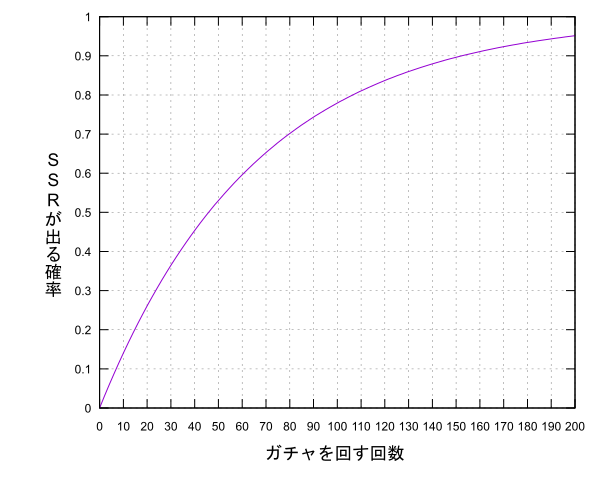
「SSRが当たるまでガチャを引くのをやめない」という心意気のプロデューサーは恐らく全国各地にいることでしょう。推しの子のSSRが登場したら「その子を当てるまで俺はガチャを回すぞ」という熱心なプロデューサーもたくさんいると思います。「出るまで回すから実質100%当たる」という狂えるプロデューサーもいくらかいるようですが、多くのプロデューサーは差こそされどアイドルへ投資できる金額が限らているのでガチャも一定回数しか回せません。ここで疑問なのですが、$x$回以内にSSRを引くことができる確率はどのくらいなのでしょうか。
まず、$x$回目にSSRが初めて出る確率について考えます。当たる確率は1.5%なので次の式で表せます。
f(x)=0.015 \cdot 0.985^{x-1}
次に$x$回目「まで」にSSRが出る確率について考えます。これは「1回目で引く確率」、「2回目で引く確率」、…、「$x$回目で引く確率」を足したもの、すなわち$f(1),f(2),...,f(x)$の総和で求められるのでそれを$F(x)$とおくと
\begin{align}
F(x) & =\sum_{k=1}^x 0.015 \cdot 0.985^{k-1} \\
& =1-0.985^x
\end{align}
となります(累積分布関数)。これは等比数列の和として計算することで値を求めることができます。さて、せっかくですのでこの$F(x)$をグラフにしてみましょう。(暗黒微笑)
デレステのガチャでは約70回回すとSSRを引ける期待値が1を超える、平均して1枚手に入る計算ですがこのグラフから分かるように70回引いても3割強の人はSSRを手に入れることができません。無慈悲ですね。
回数を重ねても当たる確率は思ったより上がらず、100回ガチャを回しても(3万円弱)約22%の人はSSRを手にすることができません。5人に1人は3万円使ってもSSRが手に入らないと考えるとアイドルへの投資はとてもシビアなものであるように思えてきます。知らなかった方が幸せだったかもしれません。
一般に成功確率$p$のベルヌーイ試行に対し初めて成功の事象$S$が出現するまで試行を繰り返すとき$x$回目で$S$が出現する確率は
f(x)=p(1-p)^{x-1}
で表せ、これを満たす確率分布を「幾何分布」と言います。この式は等比数列の形であり、等比数列は幾何数列とも言うらしくこういう名前になったとか。
また、ガチャなんかを考えるときは$x$回目にピンポイント当たる確率よりも$x$回「以内」に当たる(発生する)確率が知りたいので、その場合は$x$までの幾何分布による確率の和を考えればよくて
\begin{align}
F(x) & =P(X \leq x) \\
& =\sum_{k=1}^x p \cdot (1-p)^{k-1} \\
& =1-(1-p)^x
\end{align}
の式で表せます。このようにある値以下で発生する確率$F(x)$を累積分布関数と言います。
正規分布
ここまで紹介した「二項分布」、「ポアソン分布」、「幾何分布」はいずれも離散型の確率分布でした。次に紹介する「正規分布」は連続型の確率分布で、統計学では最も重要(らしい)な確率分布です。なので紹介します。
正規分布は次の式で与えれます。またしても唐突
f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\frac{(x-\mu)^2}{2\sigma^2}\right\} \qquad (-\infty<x<\infty)
「なんだこの式は…意味不明だ…」となりますね。僕はなりました。でも統計学ではこの式で表される分布が信仰を集めているみたいです。(こんなてきとーなこと書いたらその道の人に怒られてしまいそうだ)
さて、真面目にいきますか。この式の$x$は少し前に紹介した連中と違い連続的な値となってます。小数とかokです。次に$\mu$と$\sigma$は何なんだという話ですが、確率変数$X$が上の式$f(x)$で表される確率密度関数に従うとき、期待値$E(X)$と分散$V(X)$は次の値になります。(計算したくないので結果だけ!スマン!)
- $E(X)=\mu$
- $V(X)=\sigma^2$
意味不明な正規分布の式から思ったより綺麗な値が出てきます。この結果から$\mu$は期待値(平均)、$\sigma^2$は分散を表していることが言えます。
このことから$f(x)$は平均$\mu$、分散$\sigma$の正規分布と言われ、$N(\mu,\sigma^2)$で表されます。
正規分布は「ガウス分布」とも言われています。余談ですが期待値や分散を求める際に積分を行うのですがその計算過程で「ガウス積分」というちょっとトリッキーな感じの積分を用いることになります。(微積分の講義で少し扱ったりするかも?)
他にもいろいろな名前の確率分布がありますがキリがないのでカット(僕の推しの確率分布が紹介されてないぞ!って人がいたらごめんなさい)
独立な確率変数の和と再生性
統計学では測定した値の平均をとる場合など、確率変数の和を考える事が多いです。そこで、2つの独立な確率変数$X,Y$の和$X+Y$について考えてみます。独立であると仮定していますが、これは独立でない確率変数の和は求めるのがしんどいらしいというのが理由みたいです。まずは期待値と分散について考えてみます。
期待値と分散
独立な2つの確率変数$X,Y$の和$X+Y$の期待値と分散について次の式が成り立ちます。
- $E(X+Y)=E(X)+E(Y)$
- $V(X \pm Y)=V(X)+V(Y)$
期待値に関しては$X,Y$が独立である必要はありませんが分散は$X,Y$が独立である必要があります。また、分散の場合は$X+Y$と$X-Y$どちらの場合でもそれぞれの分散の和になります。
複数の確率変数$X_1,X_2,...,X_n$の場合でも同様の事が言えます。特に$X_1,X_2,...,X_n$が同じ確率分布に従うとしその期待値と分散が$\mu,\sigma^2$だとすると$E(X_1)=E(X_2)=...=E(X_n)=\mu,V(X_1)=V(X_2)+...=V(X_n)$となり、
- $E(X_1+X_2+...+X_n)=n\mu$
- $V(X_1+X_2+...+X_n)=n\sigma^2$
が成り立ちます。さらに、$\overline{X}=\cfrac{X_1+X_2+...+X_n}{n}$に対しては期待値と分散の性質より
- $E(\overline{X})=\mu$
- $V(\overline{X})=\cfrac{\sigma^2}{n}$
が成り立ちます。この結果は推測統計学で利用される重要なものとなっています。後でまた出てくると思います。
再生性
確率変数の和$X+Y$の期待値と分散について考えたので次は確率分布について考えます。基本的に確率分布の和を求めるのはハードみたいなんですが特定の分布の和に関しては以下が成り立つみたいです。
二項分布の場合
Bi(n,p)*Bi(m,p)=Bi(n+m,p)
$X$,$Y$が独立でそれぞれ$Bi(n,p)$,$Bi(m,p)$に従うとき、$X+Y$は$Bi(n+m,p)$に従います。
正規分布の場合
N(\mu_1,\sigma_1^2)*N(\mu_2,\sigma_2^2)=N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)
$X$,$Y$が独立でそれぞれ$N(\mu_1,\sigma_1^2)$,$N(\mu_2,\sigma_2^2)$に従うとき、$X+Y$は$N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)$に従います。
このように確率変数の和の分布を考えた時に別の分布じゃなくて足す前と同じ種類の分布が得られる性質を「再生性」と言います。再生性があると確率変数の和が考えやすくなるので結構うれしいみたいです。特に正規分布の再生性に関しては後で説明する予定の統計的推測で利用されてたり。
大数の法則と中心極限定理
堅苦しい話がだらだらと続いていますが、まだ終わりません。スイマセン
大数の法則
同じ回数ガチャを回しても当たるSSRの数が違うことは言うまでもありませんし実際友達の方がたくさんSSR持ってたりしますよね。妬ましい
さて、ここでガチャを回す回数をどんどん増やしていったらどうなるんでしょうか?感覚的には公式に告知されている1.5%で落ち着くような気がします(1.5%が正しければ)。
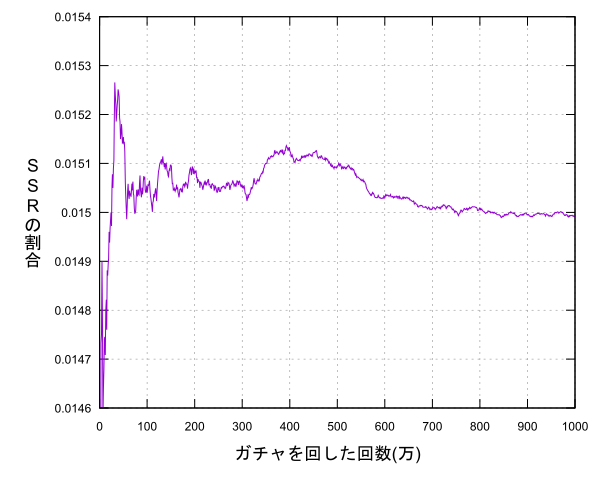
何万回とガチャを回して実際にどうなるか確かめてみたいのは山々ですがあいにく僕はそれができるだけの財力がないのでプログラムを用意してシミュレーションしてみたいと思います。せっかくなのでソースコードも載せておきます。C++を使いました。
# include <iostream>
# include <random>
int main()
{
std::random_device rd;
std::mt19937 mt(rd());
std::uniform_int_distribution<int> gatya(1, 1000);//SSRが出る確率1.5%より15以下のとき当たりとする
int size = 10000000;
int T = 0;
for (int i = 1; i <= size; i++) {
if (gatya(mt) <= 15) {
T++;
}
if (i % 10000 == 0) {
std::cout << i / 10000 << " " << static_cast<double>(T) / i << std::endl;
}
}
return 0;
}
乱数を利用して1~1000までの値を生成し15以下ならSSRを引いた(当たり)、それ以外なら引けなかった(外れ)とし、1000万回引き、1万回ごとにSSRを引いた割合を出力しそれをグラフにようと思います。(1000万連は実際に回すと300億円ってところですかね…)
試してみた結果次のようになりました。
回数を重ねるとどんどん公式に告知されている確率に近づいているように思えます。このように回数を重ねていったときに真の値の周辺に集中していく(完全に一致するわけではない)ことを大数の法則と言います。
中心極限定理
いよいよ大詰め、やたらと名前がかっこいい中心極限定理の話です。
大数の法則では標本(取ったデータ)の大きさ$n$が十分大きければその平均(標本平均)$\overline{X}$が元の分布(母集団)の平均(母平均)$\mu$の近くに集まっていくという内容でしたが、中心極限定理はその更に上を行く内容で「$n$が大きければ標本の和$X_1+X_2+...+X_n$が正規分布に近似できる」という内容です。もう少し具体的に言うと、母集団が平均$\mu$、母分散$\sigma^2$であるときどんな母集団でも$X_1+X_2+...+X_n$は$N(n\mu,n\sigma^2)$に、さらに言えば標本平均$\overline{X}=\cfrac{X_1+X_2+...+X_n}{n}$は期待値と分散の性質より$N(\mu,\cfrac{\sigma^2}{n})$に従います。「どんな母集団でも」というのがヤバいポイントです。(例外はあるらしい…?)
特に標本平均の方は$n$を大きくすると分散が0に近づくので、これは標本平均は$\mu$に近づくという事を示しています。なので、中心極限定理は大数の法則をより詳しく説明しているものであると言う事もできます。
さて、文章であれこれ書いてもイマイチな感じがするので試してみましょう。デレステのガチャを10000回回したものを標本とします。つまり$X_1+X_2+...+X_{10000}$を考えます。これを10000回行って$X_1+X_2+...+X_{10000}$の各値(当たったら1,外れたら0として計算)が出た割合を求めてそれをプロットし正規分布と比較します。ソースコードはこんな感じです。
# include <iostream>
# include <vector>
# include <random>
int main()
{
std::random_device rd;
std::mt19937 mt(rd());
std::uniform_int_distribution<int> gatya(1, 1000);//SSRが出る確率1.5%より15以下のとき当たりとする
int size = 10000;//確率変数X_sum=X_1+X_2+…+X_n(n=sizeのときのSSRの枚数)
int loop = 10000;//試行回数
std::vector<int> count(size + 1, 0);
for (int i = 0; i < loop; i++) {
int T = 0;
for (int j = 0; j < size; j++) {
if (gatya(mt) <= 15) {
T++;
}
}
count[T]++;
}
for (int i = 0; i <= size; i++) {
std::cout << i << " " << static_cast<double>(count[i]) / loop << std::endl;
}
return 0;
}
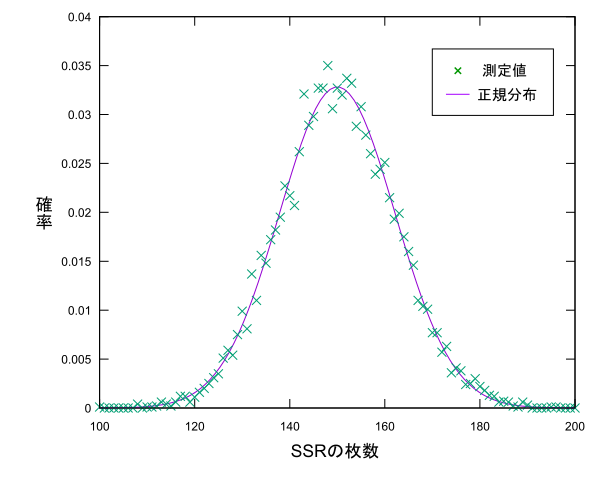
今回の母集団は$Bi(10000,0.015)$なので母平均$\mu$と母分散$\sigma^2$は次のようになります。
\begin{align}
E(X_1+X_2+...+X_{10000}) & = np=150 \\
V(X_1+X_2+...+X_{10000}) & = np(1-p)=147.75
\end{align}
なので、$X_1+X_2+...X_{10000}$の分布は$N(150,147.75)$で近似できるみたいです。では、プロットしてみましょう。
スペースの都合上$100 \leq x \leq 200$の部分を載せています。グラフにしてみると確かに正規分布っぽいですね。推測統計学では正規分布が信仰されているみたいですが、その理由はこの中心極限定理の存在みたいです。特に$\overline{X}$が$N(\mu,\cfrac{\sigma^2}{n})$に近似できる事は推測統計学において母平均を推定する場合に利用されます。
ここらでそろそろ推測統計学の話に入りましょう。何が悲しいってここまでほぼ全部確率の話でまだ統計の話に入れていないという事です。(ここまで読んでくれている人が果たして何人いるのか…
推測統計学再び
最初に述べたような気がしますが、推測統計学は手に入れたデータ(標本)から母集団の性質を推定するのが大きな目的となっています。調べたい母集団はいろいろ考えられますが、母集団を実際に調べると調べるたびに異なる値が得られると考えられます(例えば身長など)。なので得られる値を$X$とすると、$X$は確率変数であると考える事ができます。この時、確率変数$X$が従う分布を母集団分布と言います。母集団分布の性質は平均や分散、その他様々な値で定められます。このような値を**母数(パラメータ)**と言い、母集団の性質を推定するとは具体的に言えば母集団分布の母数を推定する事であると言えます。
母集団から大きさ$n$の標本を取り、その標本平均$\overline{X}=\cfrac{X_1+X_2+...+X_n}{n}$について考えてみましょう($X_1,X_2,...,X_n$は調べた各要素で、これも調べるたびに得られる値が変わるのでそれぞれ確率変数です)。標本平均は調べるたびに値が変わるので確率変数であると考えることができます。標本平均のような標本によって値の変わる確率変数を統計量といい、統計量に対しても確率分布を考えることができます。
母集団の平均が$E(X)=\mu$であるとすると、確率変数の和のところで少し話しましたが$E(\overline{X})=\mu$が成り立ちます。また、$n$の値が増えると大数の法則や中心極限定理より$\overline{X}$が$\mu$に近づいていくことから、$\overline{X}$を調べると$\mu$を調べることができると考えられます。標本平均のような母数を推定するための統計量を推定量と言います。標本平均$\overline{X}$は母平均$\mu$を推定するための推定量です。さらに、実際に標本を得て定まった値を推定値と言います。
例えば母集団の平均値$\mu$を標本から推定するときに推定量として標本平均や中央値など様々な値が考えられます。しかし、この中でどの値が推定に用いるのに適しているかという基準が無いと適切に推定をすることができません。なので、推定量の性質について考えておきます。この基準にもいろいろあるのですがとりあえず不偏性と一致性について触れておきます。
不偏性
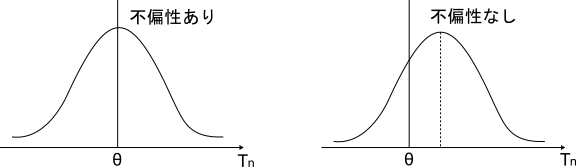
大きさ$n$の標本から得られる推定量$\hat{\theta}$の平均(期待値)がその値が母数$\theta$に等しくなる時$\hat{\theta}$は不偏性を持ち、$\hat{\theta}$は母数$\theta$の不偏推定量といいます。式にすると
E(\hat{\theta})=\theta
となります。これは推定量$\hat{\theta}$が母数$\theta$を中心に分布が広がっていることを示しています。$\theta$の値を推定したいんだから推定量も$\theta$の近くにあることが言える方が良いよねって感じです。図で表現するとこんな感じです。
母平均$\mu$、母分散$\sigma^2$の母集団分布から得た標本$X_1,X_2,...,X_n$の標本平均$\overline{X}=\cfrac{X_1+X_2+...X_n}{n}$は少し前に述べたように$E(\overline{X})=\mu$が成り立ちます。なので標本平均は母平均の不偏推定量であるといえます。また、以下の式で表される$s^2=\cfrac{(X_1-\overline{X})^2+(X_2-\overline{X})^2+...(X_n-\overline{X})^2}{n-1}$を不偏分散といいます。計算は省略しますが$E(s^2)=\sigma^2$を満たすので$s^2$は母分散$\sigma^2$の不偏推定量であるといえます。なので「不偏」分散という名前になっています。普通、分散を求める場合は$n$で割りますが不偏分散は$n-1$で割るというところが注意点です。$n$で割った場合は(不偏でない)標本分散$S^2$と呼ばれますが$E(S^2)\neq\sigma^2$となり$S^2$は母分散$\sigma^2$の不偏推定量ではありません。
一致性
大きさ$n$の標本から得られる母数$\theta$についての推定量を$\hat{\theta}$とします。標本の大きさ$n$を増やしていったときに$\hat{\theta}$が$\theta$に近づくとき推定量$\hat{\theta}$は一致性を持ち、一致推定量といいます。大数の法則で触れた通り、標本平均は$n$の値を増やすと母平均$\mu$に近づいていくので標本平均は母平均の一致推定量であるといえます。
他にも漸近正規性や有効性など推定量の良さについての基準はあるのですが疲れたので省略。許して下さい。
点推定
よくわからない話をあれこれと続けてきましたがここで推測統計学でやりたかったことが何かを思い出しておきましょう。推測統計学でやりたいことは「母集団の情報(母数)を推定すること」です。推定には2種類あり点推定と区間推定というものがあります。点推定は母数はこの値であると1つの値で狙い撃つタイプの推定で、区間推定は母数はこの辺からこの辺にあると幅を持たせるタイプの推定です。
最尤推定法
代表的な点推定の方法に最尤推定法というものがあります。「尤」は「ゆう」と読みます(読めなかった顔)。例えば当たる確率が$p$のガチャを100連回した時に当たりが3回出たとしましょう。その時の確率$L(p)$は次のようになります。
L(p)={}_{100}C_3 p^3(1-p)^{97}
最尤推定法は「起こる確率が最大である事象が現実になる」という仮定(最尤原理)に基づいたもので、実際に起こった事象の確率$L(p)$が最大になる$p$の値を求めそれを推定値とするものです。$L(p)$が最大になる値を調べるためには$L(p)$を微分しそれが0になる$p$の値を求めます。実際に$L(p)$を微分すると
\begin{align}
L'(p) & = {}_{100} C_3 \left\{ {3p^2(1-p)^{97}-97p^3(1-p)^{96}} \right\} = 0 \\
& = {}_{100}C_3p^2(1-p)^{96}(3-100p) = 0 \\
p & = 0.03 \qquad (p \neq 0,1)
\end{align}
となり$p=0.03$であると推定できます。このときの$L(p)$を尤度関数と言い、求めた値(この場合だと0.03)を最尤推定値と言います。
区間推定
点推定では母数$\theta$の値をピンポイントで推定しましたが区間推定では確率を用いて母数がこの辺にあると推定します。
正規母集団の母平均の推定(母分散が分かっている場合)
例えば母集団分布が正規分布$N(\mu,\sigma^2)$の場合(正規母集団といいます)について、$\sigma^2$の値は既に分かっていますが$\mu$の値がわからないので$\mu$について推定したい場合を考えます。この場合の標本平均$\overline{X}=\cfrac{X_1+X_2+...+X_n}{n}$の標本分布は$N(\mu,\cfrac{\sigma^2}{n})$となります。ここで$\overline{X}$を$Z$へ標準化します。標本平均$\overline{X}$は$N(\mu,\cfrac{\sigma^2}{n})$に従うので
Z=\cfrac{\overline{X}-\mu}{\sqrt{\cfrac{\sigma^2}{n}}}
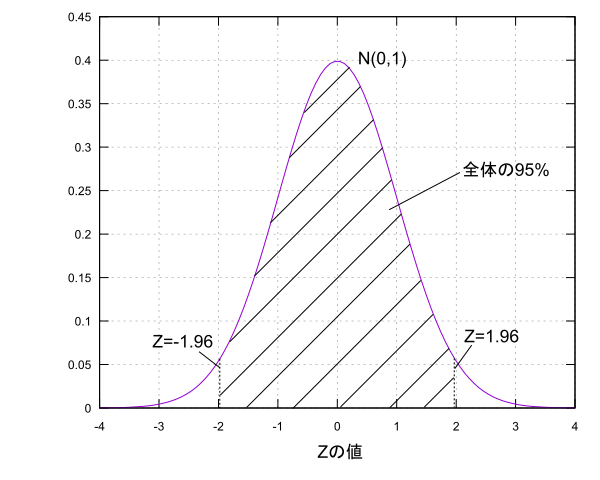
とします。標準化を行ったので$E(Z)=0,V(Z)=1$となり、Zは正規分布$N(0,1)$に従います。$Z$の分布に関して平均値を中心に全体の面積の95%の範囲の値について考えます。図にするとこんな感じです。
面積が95%というのは標本を得て$Z$を求めた時に$Z$がその範囲に95%の確率で入ることを意味しています。この時の95%を信頼度と言い、その区間を信頼区間と言います。ちなみに$N(0,1)$の95%信頼区間は$-1.96 \leq Z \leq 1.96$です(99%信頼区間の場合は$-2.58 \leq Z \leq 2.58$)。ここから$\mu$に関する式を導いていきましょう。
-1.96 \leq Z \leq 1.96 \\
-1.96 \leq \cfrac{\overline{X}-\mu}{\sqrt{\cfrac{\sigma^2}{n}}} \leq 1.96 \\
-1.96\sqrt{\cfrac{\sigma^2}{n}} \leq \overline{X}-\mu \leq 1.96\sqrt{\cfrac{\sigma^2}{n}} \\
\overline{X}-1.96\sqrt{\cfrac{\sigma^2}{n}} \leq \mu \leq \overline{X}+1.96\sqrt{\cfrac{\sigma^2}{n}}
この式は95%の確率で成り立つ式であり、信頼度95%の信頼区間であると言えます。これは100回標本を得ては同じ計算をして不等式を100回求めた時にそのうちの95個の不等式の中には$\mu$があるという意味になります。こんな感じで信頼度という形で区間の幅を決めて母数がこのくらいであると推定するのが区間推定です。せっかくなので母平均$\mu$の区間推定についてもう少し考えてみましょう。
正規母集団の母平均の推定(母分散がわからない場合)
さっきは母集団分布$N(\mu,\sigma^2)$に関して母分散$\sigma^2$がわかっているという仮定で母平均$\mu$の区間推定を行いましたが今度は母分散$\sigma^2$も分からない場合について考えてみます。つまり、正規母集団であるという事だけがわかっている状態です。この場合はさっきのように母分散を用いて$Z$へ標準化することができないので、$\sigma^2$の代わりに不偏分散$s^2=\cfrac{(X_1-\overline{X})^2+(X_2-\overline{X})^2+...+(X_n-\overline{X})^2}{n-1}$を用いて次の値を考えます。
T=\cfrac{\overline{X}-\mu}{\sqrt{\cfrac{s^2}{n}}}
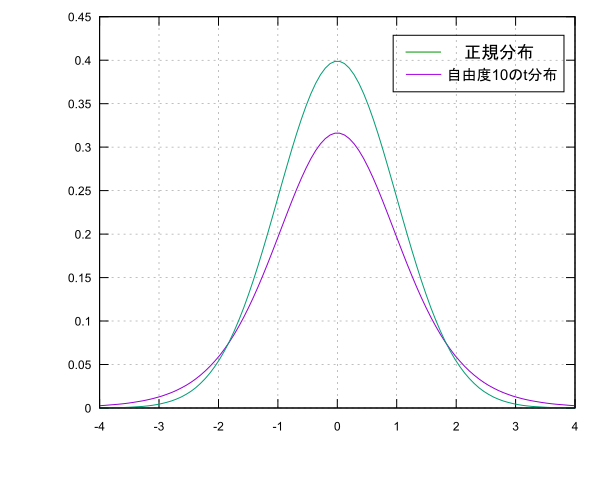
この時$T$は標準化を行ったわけではないので正規分布$N(0,1)$には従いませんが代わりに自由度$n-1$のt分布というものに従います。t分布は正規分布に似たような形をした確率分布です(すごい雑な説明)。$n$の値が大きくなると徐々に正規分布と重なっていきます。さっきと同様に母平均$\mu$の信頼度95%の信頼区間を求めると次のようになります。
\overline{X}-t(0.95)\sqrt{\cfrac{\sigma^2}{n}} \leq \mu \leq \overline{X}+t(0.95)\sqrt{\cfrac{\sigma^2}{n}}
ここで$t(0.95)$は自由度$n-1$のt分布の0を中心として面積が全体の95%となるような$T$の値です。ちなみに自由度10のt分布の場合$t(0.95)=2.228$となっています。正規分布の時もそうですがこの範囲の値は正規分布表やt分布表から値を探すかそれを計算してくれるソフトを用いて求めます。手計算は流石にキツいっす…
正規分布に比べると信頼区間の幅が少し広くなっている(母平均$\mu$の特定が難しい)事がわかります。これは母分散$\sigma^2$の代わりに用いた不偏分散$s^2$がデータの個数によって精度が変わってくるのでどうしても母分散より推定の材料としては弱いというのが理由です。しかし、データの個数$n$が大きくなってくると不偏分散$s^2$の精度が上がりt分布は正規分布とほぼ同じになります。
ここまで母集団が正規分布である場合(正規母集団)である場合について話してきましたが母集団が何でもかんでも正規分布であるわけではありません。例えばガチャが母集団だとすると母集団分布は当たりが確率$p$で、ハズレが確率$(1-p)$で起こる二項分布$Bi(1,p)$となります。これは当然正規分布ではありません。その場合、母数であるガチャの成功確率$p$を推定するにはどうすればよいのでしょうか。
二項分布の推定
正規母集団ではないので先ほどの2つの話のようにはいかない…しかし、まだ希望があります。「中心極限定理」の存在です。母集団が何であっても母平均$\mu$、母分散$\sigma^2$に対して標本平均$\overline{X}=\cfrac{X_1+X_2+...+X_n}{n}$の分布は$n$が大きければ$N(\mu,\cfrac{\sigma^2}{n})$で近似できます。なので当たった場合を$X=1$、外れの場合を$X=0$とし母集団分布である二項分布$Bi(1,p)$の母平均$\mu$と母分散$\sigma^2$を考えると、$\mu=E(X)=p$と$\sigma^2=V(X)=p(1-p)$が成り立ち標本平均$\overline{X}$は$N(p,\cfrac{p(1-p)}{n})$で近似できます。標本平均を正規分布で近似できたので少し前にやったように標準化して求めたい母数の不等式を導出します。
$Z=\cfrac{\overline{X}-p}{\sqrt{\cfrac{p(1-p)}{n}}}$より、信頼度95%で考えると
-1.96 \leq Z \leq 1.96 \\
-1.96 \leq \cfrac{\overline{X}-p}{\sqrt{\cfrac{p(1-p)}{n}}} \leq 1.96 \\
-1.96\sqrt{\cfrac{p(1-p)}{n}} \leq \overline{X}-p \leq 1.96\sqrt{\cfrac{p(1-p)}{n}} \\
\overline{X}-1.96\sqrt{\cfrac{p(1-p)}{n}} \leq p \leq \overline{X}+1.96\sqrt{\cfrac{p(1-p)}{n}}
となりますが不等式の左右にも$p$の値がありこのままでは計算が面倒です。なので、中心極限定理から$\overline{X}$は$n$が十分大きければ母平均$\mu$になる、つまり$\overline{X}=\mu=p$になる事を利用して左右の$p$を$\overline{X}$で近似します。よって
\overline{X}-1.96\sqrt{\cfrac{\overline{X}(1-\overline{X})}{n}} \leq p \leq \overline{X}+1.96\sqrt{\cfrac{\overline{X}(1-\overline{X})}{n}}
となります。これが母数$p$の信頼度95%の信頼区間となります。長い戦いだった…
仮に500回ガチャを回して15回当たりを引けたとしましょう。この場合の$p$の信頼度95%の信頼区間は$n=500,\overline{X}=0.03$より
0.15 \leq p \leq 0.45
となります。信頼区間の話の注意点としては母数(今回なら$p$)の値は何かしらの値で定まっているので変化しません。なのでこの不等式を見た時に$p$の値は95%の確率で0.15から0,45の間にあるという意味ではなく、100回これを繰り返してできた100個の不等式のうち95個の不等式の範囲に正しい$p$の値が存在しているという意味になります。ややこしいわ
今回は二項分布の標本平均$\overline{X}$を中心極限定理を用いて近似して$p$の推定をしましたが、二項分布に限らず$n$が大きければ母集団分布の形がわからなくても中心極限定理を用いて標本平均$\overline{X}$が正規分布に近似すれば区間推定を行うことができます。中心極限定理すごいね。
仮説検定
推測統計学のメインは母集団の性質(母集団分布の母数)を推定する事であると言い点推定と区間推定の話をしましたが、実は推定の他に仮説検定というものがあります。
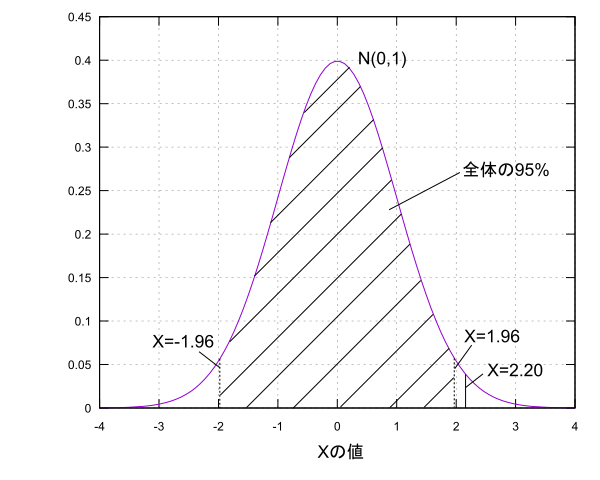
例えば「デレステのガチャでSSRが出る確率は1.5%ではない!」というような仮説を立ててそれが正しいかどうかを考えるのが仮説検定です。どうやって判断するのさ?っていう話になりますが、ここでは仮説が正しいとした時に得られると考えられるデータに対して実際に得られたデータが確率的に出やすいのかそうでないのかで考えます。例えば母集団分布が$N(\mu,1)$の形であることがわかっている場合に$\mu=0$と仮定したときに標本$X$を取ったらその値が2.2だったとしましょう。そして、母平均を中心に確率95%の範囲内なら出やすくそうでなければ仮説のもとでは出にくいと基準を決めます。すると、2.2という値は95%の範囲である$-1.96 \leq X \leq 1.96$の外にありこの仮説からは出にくい範囲にあるという事が言えます。
なので、仮説$\mu=0$が間違っていて$\mu \neq 0$であるという結論を下します。このように仮説を立て標本を手に入れ、予め定めておいた起こりやすい範囲と起こりにくい範囲のどちらに標本が存在するのかで仮説が正しいか間違っているかの判断を下します。これが仮説検定の大雑把な流れです。今回の例の仮説$\mu=0$の事を帰無仮説といい、そうではない$\mu \neq 0$を対立仮説と言います。また、出にくい範囲の割合(100-95)%=5%の事を有意水準といい、出にくい範囲の事を棄却域と言います。また、今回のように対立仮説を採用する場合、帰無仮説を棄却するといいます。仮説が間違っているとは言えない場合は帰無仮説を採択するといいます。
仮説検定には注意すべき事があり、仮説を採択した場合はその仮説が正しいものであるとはハッキリ言えません。帰無仮説が絶対合っているとは言えず間違ってはいない、矛盾はないだろうというくらいのノリになるみたいです。また、帰無仮説が正しいのに棄却する可能性と間違っている帰無仮説を採択する可能性の2つがあります(標本がたまたま外れた値になったという可能性があるので)。この可能性をそれぞれ第一種の誤り、第二種の誤りと言います。
あれこれ用語が出てきて「???」って感じなので試しにやってみましょう。とあるプロデューサーがデレステのガチャを300回回してSSRが2枚しか出なかったとしましょう。SSRが出る確率は1.5%となっているので期待値は4.5となり平均して4枚か5枚くらい出ると考えられますが、ずいぶん少なく感じます。なのでそのプロデューサーはガチャの確率は絶対もっと低い!と考えるでしょう。この時帰無仮説と対立仮説は次のようになります。
- 帰無仮説:デレステのガチャの確率は1.5%である
- 対立仮説:デレステのガチャの確率は1.5%より低い
帰無仮説が正しいと仮定すると母集団分布は二項分布$Bi(1,0.015)$に従うので標本平均$\overline{X}=\cfrac{2}{300}=0.0067$は中心極限定理による近似により$N(p,\cfrac{p(1-p)}{n})=N(0.015,0.0070^2)$に従うと考えられます。ここで$\overline{X}$を$Z$へ標準化すると次のようになります。
\begin{align}
Z & =\cfrac{\overline{X}-p}{\sqrt{\cfrac{p(1-p)}{n}}} \\
& = \cfrac{0.0067-0.015}{0.0070} \\
& = -1.19
\end{align}
次に$Z$の棄却域を決めます。このプロデューサー的には帰無仮説を棄却して対立仮説であるガチャの確率が告知されている1.5%より低いという事を言いたいので、値の低い方(グラフの左側)から5%を棄却域と定めます。左右両端に棄却域を取るものを両側検定、片側に取るものをそれぞれ右側検定、左側検定(まとめて片側検定)と言います。値の低い方から5%の値を調べると-1.65となります。つまり$Z \leq -1.65$が棄却域です。今回求めた$Z$は-1.19なので、残念ながら帰無仮説は有意水準5%では間違っているとは言い切れず採択されます。SSRが出る確率が1.5%のガチャを300回回して2回しかSSRが出ないっていうのは有意水準5%ではありえない話ではないみたいです、ドンマイ。
おわりに
確率の話から始まり推測統計学における推定と仮説検定の話まで駆け抜けました。疲れたのでこの辺でいったん終わりにしようと思いますが実際には確率論でも統計学でも触れてない話がまだたくさんあります。興味があったら触れてみると楽しいかもしれません。
気付いたらすごい長い記事になってしまいましたが、読んでくれた人や少しでも興味を持ってくれた人がいたら嬉しいです。ありがとうございました。
明日の記事は阿部ちゃん(@abe10010111000)です。よろしくお願いします。
参考文献
- 統計学入門, 東京大学出版会, 2013年
- 統計解析がわかる, 技術評論社, 2010年
- 統計学の時間 統計Web