はじめに
この記事は、Python Advent Calendar 2015 17日目の記事です。
またまた数学 Advent Calendar 2015と、ADVENTARの方のPythonとMathの17日目を兼ねていますm(_ _)m
ここでやること
2015年センター試験数学IAを全てプログラム(Python)で解くのインスパイア記事です。
ここでやってることがめちゃくちゃ楽しかったので、自分もSympyの勉強も兼ねて数学ⅡBの方をやってみました。
大学入試センター試験|解答速報2015|予備校の東進
数学II・数学B http://www.toshin.com/center/sugaku-2b_mondai_0.html
※ この記事のセンター試験の問題はここから引用しています。
実行環境
- Mac OSX 10.11.1
- Python 3.5.0
- Anaconda 3-2.4.0
- Jupyter
レポジトリ
Sympyの基本的な使い方
まずは、この後たくさん出現してくるSympyの使い方をまとめておきます。
Sympyとは?
Pythonの記号計算ライブラリ
公式ドキュメント : http://www.sympy.org/en/index.html
日本語訳 : http://turbare.net/transl/scipy-lecture-notes/index.html
Symbols - 変数定義
In [1]: from sympy import *
In [2]: x + 1
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-2-4cf92658b648> in <module>()
----> 1 x + 1
NameError: name 'x' is not defined
In [3]: x = symbols('x')
In [4]: x + 1
Out[4]: x + 1
expand - 展開
In [5]: expand((x + 1)**2)
Out[5]: x**2 + 2*x + 1
factor - 因数分解
In [6]: factor(x**4 - 3*x**2 + 1)
Out[6]: (1 + x - x**2)*(1 - x - x**2)
simplify - 簡約
In [7]: simplify((x**3 + x**2 - x - 1)/(x**2 + 2*x + 1))
Out[7]: x - 1
limit - 極限
In [8]: limit(x, x, oo)
Out[8]: oo
diff - 微分
In [9]: diff(cos(x), x)
Out[9]: -sin(x)
In [10]: diff(x**3 + x**2 - x - 1, x)
Out[10]: 3*x**2 + 2*x - 1
integrate - 積分
In [11]: integrate(cos(x), x)
Out[11]: sin(x)
In [12]: integrate(x**3 + x**2 - x - 1, x)
Out[12]: x**4/4 + x**3/3 - x**2/2 - x
Matrix - 行列
In [13]: Matrix([[1, 2, 3], [-2, 0, 4]])
Out[13]:
Matrix([
[ 1, 2, 3],
[-2, 0, 4]])
solve - 式を解く
In [14]: solve(x**2 - 1, x)
Out[14]: [-1, 1]
実際に解いてみる
第1問 - 三角関数、指数・対数関数
座標の問題はSympyのMatrixを用いて各点をベクトルに落とし込んで考えればOK.
とりあえずθは便宜上45°と置いて考えてみましょう。
import math
import sympy as sy
import numpy as np
γ = sy.pi/4
O = sy.Matrix([0, 0])
P = sy.Matrix([2*sy.cos(γ), 2*sy.sin(γ)])
Q = sy.Matrix([2*sy.cos(γ) + sy.cos(7*γ), 2*sy.sin(γ) + sy.sin(7*γ)])
2つの点の距離は、the Norm of a Matrixという概念で表現できます。
http://docs.sympy.org/0.7.2/modules/matrices/matrices.html#sympy.matrices.matrices.MatrixBase.norm
(O - P).norm()
(P - Q).norm()
2 # ア
1 # イ
次の$OQ^2$は愚直に計算するしかないようです。
この計算はθの値に依存するので、先ほど置いた45°は使えない...新しくθをSymbol化して定義しましょう。
# 0より大きい値としてθをSymbol化
θ = sy.symbols('θ', positive=True)
sy.simplify((2*sy.cos(θ) + sy.cos(7*θ))**2 + (2*sy.sin(θ) + sy.sin(7*θ))**2)
4*cos(6*θ) + 5 # ウ, エ, オ
simplifyしてあげたら、いい感じに答えを導き出せました。
次はOQの最大値を考えます。
これちょっと面倒そうなので、解答欄[カ]が整数1桁ということを利用して総当りで計算するという解法でいきます。
for n in range(4, 9):
γ = math.pi / n
print("θがπ/"+ str(n) + "のとき、OQ**2の値は" + str(5 + 4*np.cos(6*γ)))
θがπ/4のとき、OQ**2の値は5.0
θがπ/5のとき、OQ**2の値は1.7639320225
θがπ/6のとき、OQ**2の値は1.0
θがπ/7のとき、OQ**2の値は1.39612452839
θがπ/8のとき、OQ**2の値は2.17157287525
めでたく θ = π/5 のときに最大値を取ることがわかりました。
[カ] : 5
その時とる値が1.7639320225となりました。
この値が直感的になんの平方根かわかると思いますが、念のため計算しておきましょう。
from fractions import Fraction
# 分母が1以下の最適な分数を求めてる
Fraction(1.7639320225**2).limit_denominator(1)
Fraction(3, 1)
$1.7639320225^2 ≒ 3$ ということが判明したので、[キ]の値も求まりました。
[キ] : 3
直線OPを表す方程式は暗算でもわかるので割愛。[ク]
(\sin\theta)x - (\cos\theta)y = 0
3点O, P, Qが一直線上になるので、上記の式に点Qの座標を代入してあげればOK.
sy.simplify(sy.sin(θ)*(2*sy.cos(θ)+sy.cos(7*θ))-sy.cos(θ)*(2*sy.sin(θ)+sy.sin(7*θ)))
-sin(6*θ)
# _は直前の出力値を受け取る
sy.solve(_)
[pi/6] # ケ
はい次!
これはめっちゃ簡単。角OQPが直角になるのは、OP = 2, PQ = 1 より
[コ] : $OQ = \sqrt3$
この値と[ウ][エ][オ]で求めたOQの値を用いて、角OQPが直角になるの時のθを求める。
# 5+4*sy.cos(6*θ) = 3 より
sy.solve(5+4*sy.cos(6*θ) - 3)
[pi/9, 2*pi/9]
$\pi/8 \leqq θ \leqq \pi/4$ なんで、$θ = 2/9\pi$ [サ][シ]
import math
import sympy as sy
import numpy as np
x, y, a, b = sy.symbols('x y a b', real=True, positive=True) # 正の実数としてsymbol化
c1 = x**2*y**3 - a**2
c2 = x*y**3 - b**3
sy.solve({c1, c2}, {x, y})
[{y: b**2/a**(2/3), x: a**2/b**3}] # ス, セ, ソ, タ
solveを利用して一瞬で解決できました!
あとはyの値に注目して、pの値を求めます。[チ][ツ][テ]
$p = -2/3$
上記で算出したxとyに、b = 2*a**(4/3)をそれぞれ代入してあげればOK.
まずはxから。
sy.simplify(a**2/(2*a**(4/3))**3)
a**(-2.0)/8 # ト, ナ
そしてyの方も。
sy.simplify((2*a**(4/3))**2/a**(2/3))
4*a**2.0 # ニ
ここでx + y の最小値を考える時に、Scipyの力を使えば「相加平均と相乗平均の関係」なんて公式を覚えておく必要はないんです!
from scipy.optimize import differential_evolution
# symbolであるaを、数値として扱えるように変換
numeric_a = sy.lambdify(a, a**(-2.0)/8 + 4*a**2.0)
# a の範囲が a > 0 なんで、上限はpython2系でのint最大値とでもしておく
# 力技で a が 0 ~ 2147483647 までの間の最小値を求める
differential_evolution(numeric_a, [(0, 2**31-1)])
nfev: 518
success: True
nit: 33
jac: array([ 7.06101844e-06])
message: 'Optimization terminated successfully.'
fun: array([ 1.41421356])
x: array([ 0.42044842])
この結果より、
「a = 0.42044842 のときに、x + y は最小値 1.41421356 を取る」ことがわかる。
あとは、「0.42044842 が2の何乗のなのか」と、「1.41421356 が何の平方根なのか」を計算すればOK.
from fractions import Fraction
math.log2(0.4204482)
Fraction(_).limit_denominator(9)
Fraction(-5, 4) # ネ, ノ, ハ
Fraction(1.41421356**2).limit_denominator(1)
Fraction(2, 1) # ヌ
やっと第1問終わった(´-ω-`)
第2,3,4問は省略して、
_人人人人人人人_
> 突然の第5問 <
 ̄Y^Y^Y^Y^Y^Y^Y^ ̄
※ 余裕ができ次第、追記していきます。
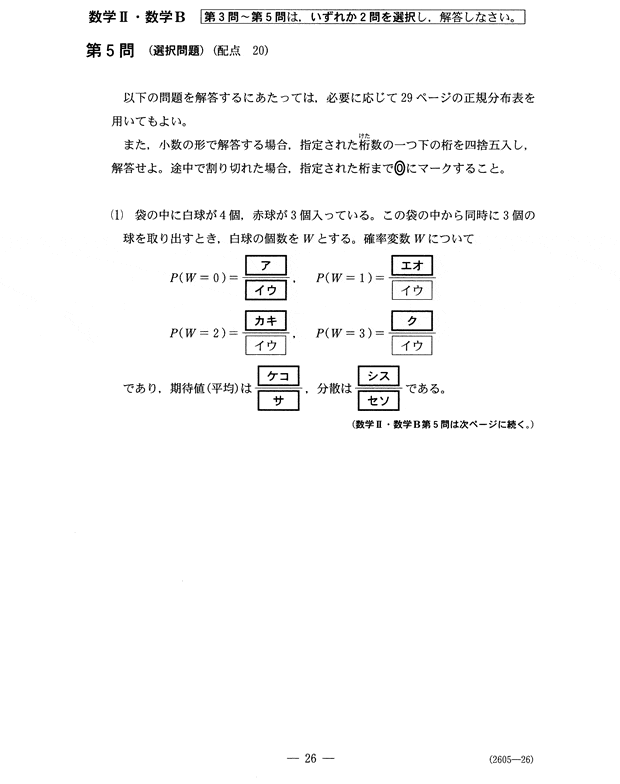
第5問 - 確率分布と統計的な推測
組み合わせの計算は、Scipy.misc.combというモジュールを使えば簡単。
http://docs.scipy.org/doc/scipy/reference/generated/scipy.misc.comb.html#scipy.misc.comb
import itertools
import scipy.misc as scm
scm.comb(7, 3, exact=True)
35 # イ, ウ
scm.comb(4, 0, exact=True)*scm.comb(3, 3, exact=True)
scm.comb(4, 1, exact=True)*scm.comb(3, 2, exact=True)
scm.comb(4, 2, exact=True)*scm.comb(3, 1, exact=True)
scm.comb(4, 3, exact=True)*scm.comb(3, 0, exact=True)
1 # ア
12 # エ, オ
18 # カ, キ
4 # ク
# 期待値と分散を計算するためにディクショナリに格納
dict = {0: 1/35, 1: 12/35, 2: 18/35, 3: 4/35}
mean = sum(x*y for x, y in dict.items())
from fractions import Fraction
Fraction(mean).limit_denominator(9)
Fraction(12, 7) # ケ, コ, サ
variance = sum(x*x*y for x, y in dict.items()) - mean**2
Fraction(variance).limit_denominator(99)
Fraction(24, 49) # シ, ス, セ, ソ
標準正規分布が出てきましたが、これもScipyの統計ライブラリを利用すればOK.
http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.norm.html#scipy.stats.norm
from scipy.stats import norm
norm.interval(alpha=0.99)
(-2.5758293035489004, 2.5758293035489004) # タ
import sympy as sy
from scipy.stats import norm
n, σ = sy.symbols('n σ')
norm.interval(alpha=0.95)
norm.interval(alpha=0.99)
(-1.959963984540054, 1.959963984540054)
(-2.5758293035489004, 2.5758293035489004)
L1 = 2*1.96*σ/sy.sqrt(n)
L2 = 2*2.58*σ/sy.sqrt(n)
L2/L1
1.31632653061224 # チ, ツ
L3 = 2*1.96*σ/sy.sqrt(4*n)
L3/L1
0.500000000000000 # テ, ト
さいごに
Sympyの基本的な使い方さえ覚えてしまえば、センター試験のレベルくらいは簡単にできました。
今回ざっとやってみての感想はこんな感じ。
- センター試験懐かしい!(僕が受けたのは2008年なんで8年くらい前の出来事)
- 数学楽しい!
- 手計算しやすいように設けられている途中の誘導設問が逆に面倒くさい...
- Sympyかなり便利!確かに布教したくなる!
- ライブラリが豊富でお手軽に数学できちゃうPython素晴らし!
- 楽しい気づきを与えてくださったAkai_Bananaさんに感謝!!!