はじめに
前回の続きです。今回がラストになります。
楽天市場から取得した商品データの価格分析をするための前処理をしたので、今回はいよいよ簡単な分析にトライします。
- 楽天市場で販売されている野菜(今回はメークイン)の価格相場はどのくらいなのか?
- 1kgあたりの金額はいくらが妥当なのか?
といったことを、初歩的な分析スキルを使って出してみたいと思います。
方針
目的を改めて整理すると「農産物を販売するにあたっての価格調査のため」です。
農産物価格についてkgごとに集計したりグラフ化してみたりすることで、「どのくらいの価格で販売するのが妥当なのか」をある程度の根拠を持って得たいな、というのが今回の目的でした。
そのためにまず調べやすそうな楽天市場での相場を調べることで、この根拠の一つにしてみよう、という考えです。
以下のような手順で見ていきます。
(1)集計してみる
まずは入数ごとの商品価格の要約統計量(平均値、中央値など)を集計し、表にして見てみます。
つまり、重さ(1kg, 2kg…)ごとの商品価格を具体的な数値で把握してみることで、今回の分析の第一歩とします。
(2)分布を確認してみる(可視化)
入数ごとのデータを使ってヒストグラムや散布図を描いてみて、入数と商品件数や、入数と商品価格の関係がどのような分布になるかを見てみることにします。
また、商品価格の中央値に絞って可視化を行ってみることで、次の(3)の分析に繋げます。
(3)線形近似してパラメータを求める
入数と価格の中央値の関係を1次関数(直線)と見立ててその式のパラメータを求めてみます。
先ほど入数ごとの価格の中央値に着目して可視化したことで「入数と商品価格は1次関数の関係(グラフ上で直線)になりそう」という推測が生まれます。これは実際に当てはめると、商品価格は「送料や箱代・作業代などのベースとなる金額」に「1kgあたりの金額」が加算されて商品代が決められる、と考えることができます。
関係式のパラメータを求めることで、その「ベースとなる金額」と「1kgあたりの金額」を算出してみます。
集計と分析
集計に入る前に、データの準備をしておきます。
前回の最後に保存した加工済みのデータをcsvファイルから読み込んでDataFrameに入れておきます。
df = pd.read_csv('20200914_rakuten_mayqueen_2.csv')
(1)集計してみる
準備ができたらまずは、入数ごとの商品価格の要約統計量を調べてみます。
入数ごとの表にするためにgroupby()関数を使います。
また、統計量の表示にはdescribe()メソッドを使います。
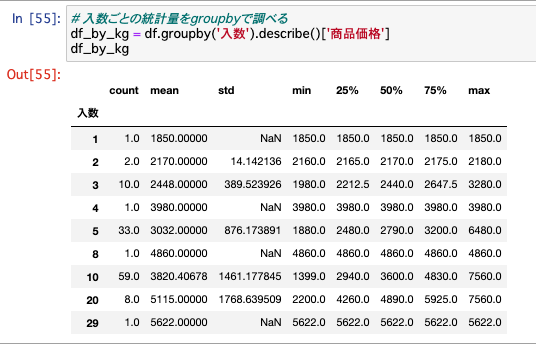
# 入数ごとの統計量をgroupbyで調べる
df_by_kg = df.groupby('入数').describe()['商品価格']
df_by_kg
この表のcount列を見てみると、1件〜2件しかデータがない行と、データ件数が多い行がそれぞれあるのがわかります。
例えば「じゃがいも1kgや2kgでの販売」はそもそも件数が少なく、「じゃがいも5kgや10kgでの販売」は件数が多い、ということがわかります。
箱の規格は大体決まっているので実際の現場からすると納得の数値なのですが、このようにデータからも確認することができました。
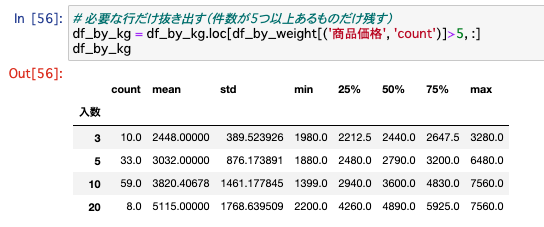
この表から、必要な行だけ抽出しておきます。今回は件数が多い行のみを活用することにします。
残す行の入数の数値を直接指定しても良いのですが、後々スクリプトを再利用する可能性も考えて、ここでは5件以上ある行(3kg, 5kg, 10kg, 20kgが該当)を抜き出してみることにします
# 必要な行だけ抜き出す(件数が5つ以上あるものだけ残す)
df_by_kg = df_by_kg.loc[df_by_weight[('商品価格', 'count')]>5, :]
df_by_kg
さらにここから、列も必要なものだけを残します。
今回は比較したい列として、「件数count」「平均値mean」「最小値min」「中央値50%」「最大値max」を残すことにしました。
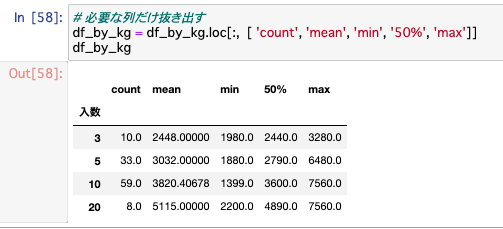
# 必要な列だけ抜き出す
df_by_kg = df_by_kg.loc[:, [ 'count', 'mean', 'min', '50%', 'max']]
df_by_kg
これで、スッキリした集計結果の表が得られました。
この表を元に、例として「じゃがいも10kg」の商品価格を見てみます。その統計量は、
- 最小値(
min) 1,399円 - 最大値(
max) 7,560円 - 平均値(
mean) 3,820円 - 中央値(
50%) 3,600円
というような金額(送料・税込)になっていました。
相場感を掴むためには平均値か中央値を参考にすれば良さそうですが、最小値と最大値の幅が大きいことから全体のバラつきが大きそうだと考えられます。そのため、参考にする数値としては平均値ではなく中央値を見ていこう、と考えます(このバラつきは次の項目で可視化して見てみます)。
ちなみに最安値のものが異様に安いので気になってみてみると、いわゆる「訳あり品」として超小玉のものが販売されているようでした。逆に最高値を見てみると特別高級なブランド品という訳でもなく一地域の商品だったのですが、2020年の6月〜8月上旬頃まではじゃがいもの相場が全国的に異様に高かったため、このような金額で出品されているのかなと思いました(あくまで推測です)。
(2)分布を確認してみる(可視化)
次は、データをもとにグラフを描いて可視化することで、よりデータを深くみていこうと思います。
まずは「ヒストグラム」を表示してみます。
ここでは入数(kg)と度数(いくつのデータがあるか)を図示します。
ヒストグラムを表示するには、matplotlibというライブラリのhist()関数を用います。
データとして集計前のDataFram(df)を指定します。
オプションにbinsを指定することで、ヒストグラムの帯の幅を変えています。ここでは1から30までの1刻みで件数を図示しています。
import matplotlib.pyplot as plt
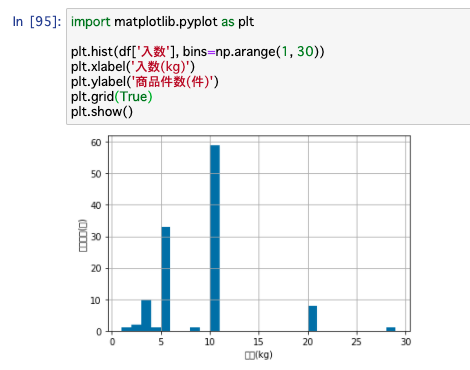
# ヒストグラム(入数と件数の関係)
plt.hist(df['入数'], bins=np.arange(1, 30))
plt.xlabel('Quantity(kg)')
plt.ylabel('Count')
plt.grid(True)
plt.show()
先ほど数値で見たことの確認になりますが、入数kgによって件数に差がありますね。5kg、10kgあたりの商品が特に多く、3kgや20kgも比較的出ているというのがわかります。
次に、「散布図」を表示してみます。
散布図を表示するには、matplotlibのscatter()関数を用います。
これも集計前のDataFram(df)を指定してみます。
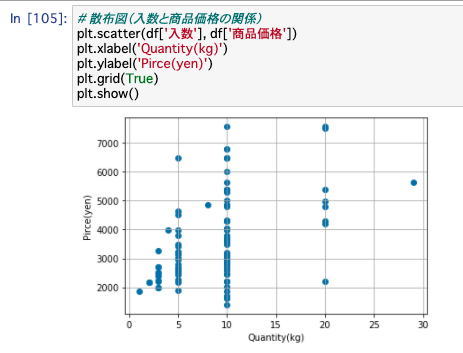
# 散布図(入数と商品価格の関係)
plt.scatter(df['入数'], df['商品価格'])
plt.xlabel('Quantity(kg)')
plt.ylabel('Pirce(yen)')
plt.grid(True)
plt.show()
何kgの商品がいくらで販売されているのかが点で表示されますが、ここで先ほど集計した時に触れた「価格のバラつき」が大きいことが目に見えてわかります。
この状態だと、バラつきが大きくて値決めの判断材料にはできなさそうです。
そこで、今度は商品価格の「中央値」に絞ってプロット図を描いてみます。
先ほどの散布図と違って、入数ごとに対応する商品価格の中央値となる1点がグラフ上にプロットされます。
ここでは集計後のDataFrame(df_by_kg)を使って図示します。
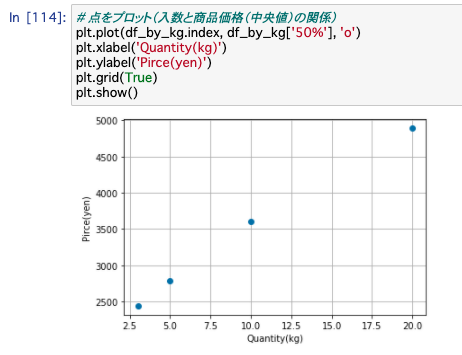
# 点をプロット(入数と商品価格(中央値)の関係)
plt.plot(df_by_kg.index, df_by_kg['50%'], 'o')
plt.xlabel('Quantity(kg)')
plt.ylabel('Pirce(yen)')
plt.grid(True)
plt.show()
プロットした点が、綺麗な直線上に並んでるように見えます。
なんだか入数と商品価格の関係を掴むことができそうです。
それぞれの点における数値(つまり中央値)は以下の通り。
野菜の販売金額を設定する際には、このぐらいの金額に設定することで、ネット販売における相場とのズレが少ない妥当な値決めができそうです。
このように、数値を見るだけでなく可視化すると直感的にわかりやすくなります。
また可視化するにしても、漠然と全体を見るだけだとバラつきが多くてどう見て良いのかよくわからなかったものが、「中央値」という1つの統計量に絞って見てみると規則性を見ることができました。
(3)線形近似してパラメータを求める
もう少し、先ほどの結果を深掘りしてみることにします。
先ほどプロットした入数kgに対する商品価格の中央値の値は、1次関数の関係に近い(グラフ上で点がほぼ直線上に並んでいる)と考えられます。
そこで「線形近似」というのを行ってみます。
近似した直線の式のパラメータ(傾きと切片)を求めることで、商品価格を詳細に見ることができそうです。
つまり、「1kgあたりの金額」はこの直線の傾きの値に該当し、「送料や箱代・作業代などのベースとなる金額」はこの直線の切片に該当します。
線形近似にはnumpyの機能を使います。
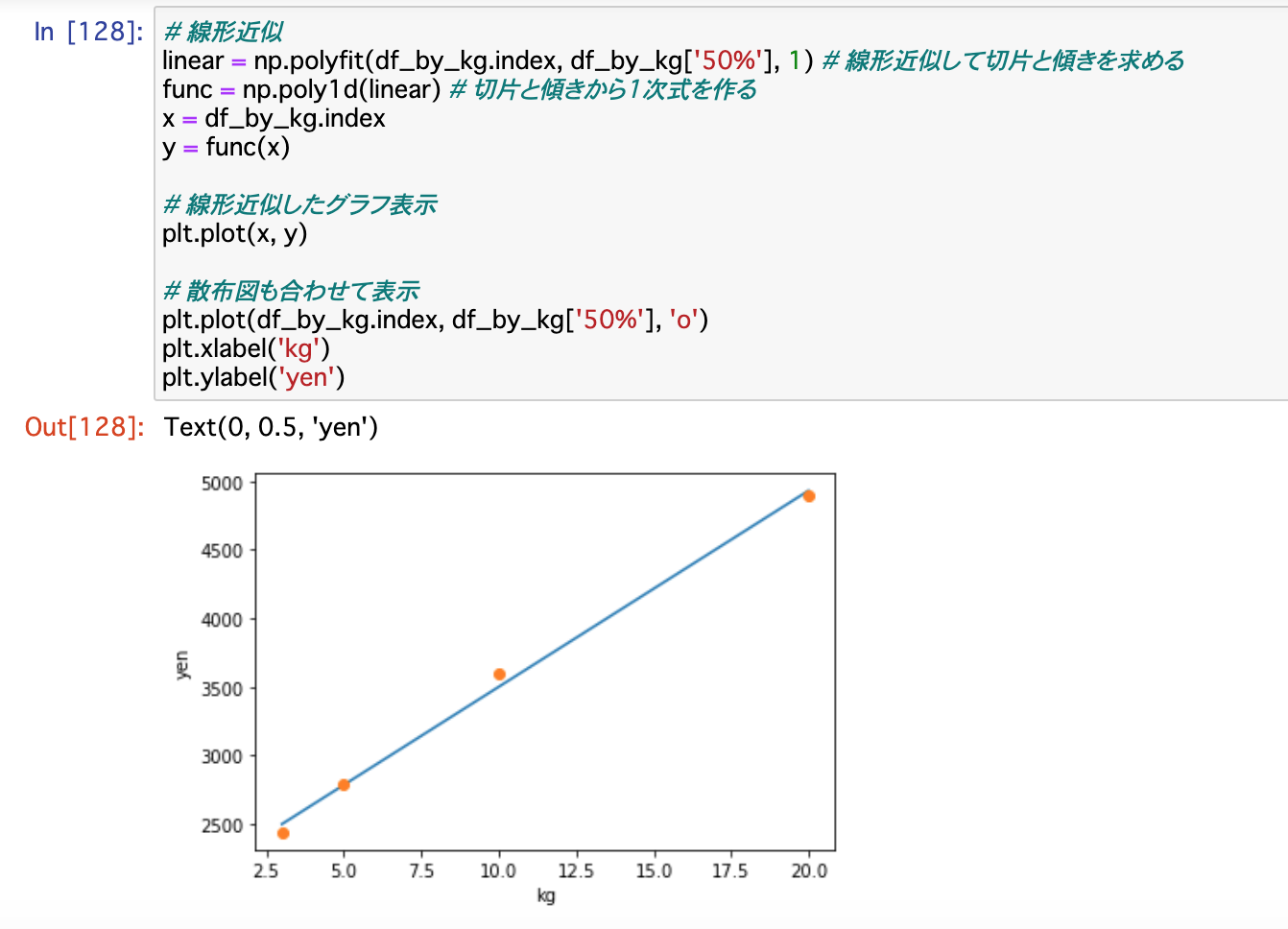
# 線形近似
linear = np.polyfit(df_by_kg.index, df_by_kg['50%'], 1) # 線形近似して切片と傾きを求める
func = np.poly1d(linear) # 切片と傾きから1次式を作る
x = df_by_kg.index
y = func(x)
# 線形近似したグラフ表示
plt.plot(x, y)
# 散布図も合わせて表示
plt.plot(df_by_kg.index, df_by_kg['50%'], 'o')
plt.xlabel('kg')
plt.ylabel('yen')
このように、プロットした点がだいたい直線に乗っていることが確認できるかと思います。
そしてこのlinear変数に、この直線の式のパラメータが入っています。
print('直線のパラメータ[傾き, 切片] = ', linear)
# -> 直線のパラメータ[傾き, 切片] = [ 142.94797688 2071.99421965]
つまり、
- ベースとなる金額(切片に該当)約 2072円
- 1kgあたり金額(傾きに該当) 約143円
この数値を使うと、例えば4kgの商品を作るとしたら、2072円 + 4kg@143円 = 2,644円 くらいで設定すると良いんじゃないか、と計算することができます。
商品価格の中央値が、ここまで綺麗に一次関数の式に近似できたのが面白かったです。
今回使用したデータ数は分析するには少なかったと思うのですが、それでも感覚的に納得できる数値を得ることができました。
おわりに
今回のような基礎的な分析でも、活用できそうな根拠のある数値を得ることができました。
このような分析結果をもとに意思決定に繫げるのが、仕事でデータ分析を活用するにあたっての肝になるのかな、と思います。
そしてそれは1回で終えるのではなく、トライ&エラーを重ねて、より正しく説得力のある分析と意思決定を行うサイクルを回していくことが大事になってくるようにも思います。
ひとつ大事な観点として、分析結果の妥当性はもうちょっと検証する必要はありそうです。
例えばデータ数をもっと増やしたり、データの中身を精査する必要があります。今回の例では、品種によって細分化したらもっと性格なデータを出せるなあと思いました。
データ分析したこの後は実際の価格決めという意思決定のフェーズに入っていくのですが、それにはまた別の視点が必要です。
少なくとも以下のことは、自身の中で固めておく必要があるなあと思います。
- 商品の価値をどう設定するのか。相場より安く設定するのか高く設定するのか。
- ターゲットは誰なのか。今回楽天市場のデータで分析したが、よりターゲットに近い市場での分析が必要かもしれない。
もうちょっとスピード感を持って意思決定できれば良いのでしょうけど、難しい。
ひとまず今回の数値を使って、近々ひとつアウトプットを出すようにしたいと思います!
さて、三回に渡ってデータ分析に関する記事を続けてきましたが、今回のテーマは一旦ここまでにします。
学んだ知識をもとに探り探りの分析だったため、もしかしたら考え方が間違っていたりよりスマートな記述の仕方があるかもしれません。
ここまで読んでいただいて、もし気になる点があればコメントいただけると大変嬉しいです!