This article is a Private article. Only a writer and users who know the URL can access it.
Please change open range to public in publish setting if you want to share this article with other users.

More than 3 years have passed since last update.

Pythonデータ解析お百度参り３８：最大公約数（ユークリッドの互除法）

Python

Last updated at 2020-10-08Posted at 2020-06-23

課題３８：最大公約数（ユークリッドの互除法）

ユークリッド平面状に２つの格子点 $P = (x_1, y_1)$, $Q = (x_2, y_2)$ がある。線分 $PQ$ 上には、$P$, $Q$ 以外にいくつの格子点が存在するか計算する関数を作ってください。またそのアルゴリズムを説明してください。

ただし、

-10⁶ ≤ $x_1$ ≤ 10⁶
-10⁶ ≤ $x_2$ ≤ 10⁶
-10⁶ ≤ $y_1$ ≤ 10⁶
-10⁶ ≤ $y_2$ ≤ 10⁶

とします。

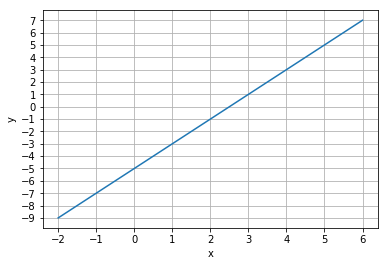
例1

x1 =  -2
y1 =  -9
x2 =  6
y2 =  7

# 図示して確認
%matplotlib inline
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot([x1, x2], [y1, y2])
ax.set_xticks(range(x1, x2 + 1, 1))
ax.set_yticks(range(y1, y2 + 1, 1))
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.grid()

例2

x1 =  -42
y1 =  -65
x2 =  62
y2 =  -91

例3

x1 =  908
y1 =  -307
x2 =  -86
y2 =  -679

課題提出方法

基本的にGoogle Colaboratoryを用いてプログラミングしてください。どうしても Google Colaboratory を用いることができない場合のみ、Jupyter Notebook または Jupyter Lab を用いてください。
課題１つごとに、ノートブックを新規作成してください。１つのノートブックで複数の課題を解かないでください。
ノートブックを新規作成すると「Untitled.ipynb」のような名前になりますが、それを「学籍番号・氏名・課題番号」のような名前に変更してください。
質問・感想・要望などございましたらぜひ書き込んでください。
もし課題を解くにあたって参考になったウェブサイトがあれば、それについても触れてください。
課題を計算し終わった ipynb ファイルを提出するときは、指定したメールアドレスに Google Drive で共有する形で授業担当者に提出してください。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up