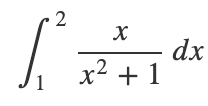問１１：区分求積法（長方形近似）

積分を数値的に求める区分求積法として、長方形近似、台形則、シンプソン則などがある。そのうち長方形近似では、ある点 $x_i$ における値 $f(x_i)$ に幅 $h$ をかけた長方形を足し合わせたものを積分値として近似する。

長方形近似を用いて、上の式を数値的に解け。

問１２：区分求積法（台形則）

積分を数値的に求める区分求積法として、長方形近似、台形則、シンプソン則などがある。そのうち台形則では、ある点 $x_i$ とその前の点 $x_{i-1}$ における、$f(x_i)$ と $f(x_{i-1})$ による幅 $h$ の台形を足し合わせたものを積分値として近似する。

台形則を用いて、上の式を数値的に解け。

問１３：区分求積法（シンプソン則）

積分を数値的に求める区分求積法として、長方形近似、台形則、シンプソン則などがある。そのうちシンプソン則では、ある点 $x_i$ とその前の点 $x_{i-1}$、後の点 $x_{i+1}$ を通る二次関数を導出し、その$f(x_{i-1})$ から $f(x_{i+1})$ までの積分値$h(f(x_{i+1})+4f(x_i)+f(x_{i-1}))/3$ を足し合わせたものを積分値として近似する。

シンプソン則を用いて、上の式を数値的に解け。

問１４：エラトステネスの篩

整数 $n$ を入力すると、 $n$ 以下の素数の個数を返す関数を作りなさい。またそのアルゴリズムを説明しなさい。

ただし、

1 ≤ $n$ ≤ 10⁶

とする。

例14-1

n = 10

例14-2

n = 100

例14-3

n = 1000

例14-4

n = 10000

例14-5

n = 100000

問１５：格子点の個数

ユークリッド平面状に２つの格子点 $P = (x_1, y_1)$, $Q = (x_2, y_2)$ がある。線分 $PQ$ 上には、$P$, $Q$ 以外にいくつの格子点が存在するか計算する関数を作りなさい。またそのアルゴリズムを説明しなさい。

ただし、

-10⁶ ≤ $x_1$ ≤ 10⁶
-10⁶ ≤ $x_2$ ≤ 10⁶
-10⁶ ≤ $y_1$ ≤ 10⁶
-10⁶ ≤ $y_2$ ≤ 10⁶

とする。

【ヒント】最大公約数を求める問題に帰着できます。「ユークリッドの互除法」で効率的に解けます。

例15-1

x1 =  -2
y1 =  -9
x2 =  6
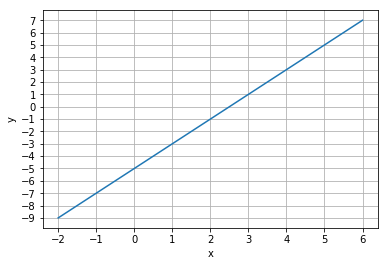
y2 =  7

# 図示して確認
%matplotlib inline
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot([x1, x2], [y1, y2])
ax.set_xticks(range(x1, x2 + 1, 1))
ax.set_yticks(range(y1, y2 + 1, 1))
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.grid()

例15-2

x1 =  -42
y1 =  -65
x2 =  62
y2 =  -91

例15-3

x1 =  908
y1 =  -307
x2 =  -86
y2 =  -679

例15-4

x1 =  -6326
y1 =  3211
x2 =  7048
y2 =  5822

例15-5

x1 =  -9675
y1 =  -2803
x2 =  3828
y2 =  -6349

参考：例の作り方

import random
x1 = random.randint(-1000000, 1000000)
y1 = random.randint(-1000000, 1000000)
x2 = random.randint(-1000000, 1000000)
y2 = random.randint(-1000000, 1000000)

print("x1 = ", x1)
print("y1 = ", y1)
print("x2 = ", x2)
print("y2 = ", y2)

プログラミング問題集（問１１〜問１５）