Sympyを用いた演算
Google Colab で使うための準備
# 現在の Google Colab では Sympy 1.1.1 が入っている。
# Sympy 1.1 では後述の「特殊解」が計算できないので、1.3 にアップグレードする。
# !pip install sympy==1.3
# 【追記(2022/01/21)】現在の Google Colaboratory では、
# Sympy の 1.7.1 が入っており、そのせいで不具合が起こるようです。
# 次のようにして 1.9 をインストールしてください。
!pip install sympy==1.9
import sympy as sym
from sympy.plotting import plot
sym.init_printing(use_unicode=True)
%matplotlib inline
# Google Colab 使用の場合、SympyによるTeX表示をサポートするために実行する
def custom_latex_printer(exp,**options):
from google.colab.output._publish import javascript
url = "https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.3/latest.js?config=default"
javascript(url=url)
return sym.printing.latex(exp,**options)
sym.init_printing(use_latex="mathjax",latex_printer=custom_latex_printer)
シンボルの定義
指定した文字をシンボル(変数を表す文字)として扱います。
a = sym.Symbol('a')
まとめて定義したいときは次のように。
a, b, c, x, y = sym.symbols("a b c x y")
指定した文字を関数として扱います。
f = sym.Function('f')
g = sym.Function('g')
簡単な多項式
# 数式は英語で numerial expression または numerical formula
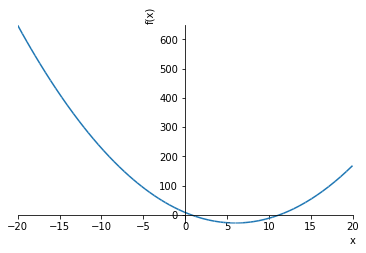
expr = x**2-12*x+8
expr
$$x^{2} - 12 x + 8$$
# 得られた関数を図示
plot(expr, (x, -20, 20))
<sympy.plotting.plot.Plot at 0x7faf57ced080>
因数分解する
# 因数分解
expr = x**2 + 2*x + 1
sym.factor(expr)
$$\left(x + 1\right)^{2}$$
方程式を解く
# 等式は英語で equation または equality
expr = x**2 - 12 * x + 8
eq = sym.Eq(expr, 0)
eq
$$x^{2} - 12 x + 8 = 0$$
# 方程式を解く
sym.solve(eq)
$$\left [ - 2 \sqrt{7} + 6, \quad 2 \sqrt{7} + 6\right ]$$
# 代数を使った式も取り扱える
eq = sym.Eq(a * x ** 2 + b * x + c, 0)
eq
$$a x^{2} + b x + c = 0$$
# xについて解く
sym.solve(eq, x)
$$\left [ \frac{- b + \sqrt{- 4 a c + b^{2}}}{2 a}, \quad - \frac{b + \sqrt{- 4 a c + b^{2}}}{2 a}\right ]$$
# 連立方程式
eq1 = 3 * x + 5 * y - 29
eq2 = x + y - 7
sym.solve([eq1, eq2])
$$ x : 3, y : 4$$
微分
expr = 2 * x ** 2 + 5 * x - 3
expr
$$2 x^{2} + 5 x - 3$$
# 微分
sym.Derivative(expr)
$$\frac{d}{d x} \left(2 x^{2} + 5 x - 3\right)$$
# 微分を計算する
sym.Derivative(expr).doit()
$$4 x + 5$$
# このように書いても同じ
sym.diff(expr)
$$4 x + 5$$
# sym.Eq を使って等式として表記
sym.Eq(sym.Derivative(expr), sym.diff(expr))
$$\frac{d}{d x} \left(2 x^{2} + 5 x - 3\right) = 4 x + 5$$
# 上と同じ意味だが、変数が1つだけなら上のように省略できる。
# 変数が2つ以上の場合は何で微分するか明記しなければいけない
sym.Eq(sym.Derivative(expr, x), sym.diff(expr, x))
$$\frac{d}{d x} \left(2 x^{2} + 5 x - 3\right) = 4 x + 5$$
# 2階微分
sym.Eq(sym.Derivative(expr, x, 2), sym.diff(expr, x, 2))
$$\frac{d^{2}}{d x^{2}} \left(2 x^{2} + 5 x - 3\right) = 4$$
# xについて微分して x=1を代入
sym.diff(expr).subs(x, 1)
$$9$$
# x について微分
expr = a * x ** 2 + b * x * y + c * y ** 2
sym.diff(expr, x)
$$2 a x + b y$$
# xについて微分して x=1を代入
sym.diff(expr, x).subs(x, 1)
$$2 a + b y$$
課題1
以下の微分の公式を、Sympy を使って完成させなさい。
【ヒント】 sin などの関数を Sympy で使うときは sym.sin のように書きます
1-1.
$$\frac{\partial}{\partial x} x^{a} = $$
1-2.
$$\frac{d}{d x} \sin{\left (x \right )} = $$
1-3.
$$\frac{d}{d x} \cos{\left (x \right )} = $$
1-4.
$$\frac{d}{d x} e^{x} = $$
1-5.
$$\frac{\partial}{\partial x} a^{x} = $$
1-6.
$$\frac{d}{d x} \log{\left (x \right )} = $$
1-7.
$$\frac{d}{d x} \sqrt{x} = $$
1-8.
$$\frac{d}{d x} \tan{\left (x \right )} = $$
1-9.
$$\frac{\partial}{\partial x} \sin^{a}{\left (x \right )} = $$
1-10.
$$\frac{\partial}{\partial x} \cos^{a}{\left (x \right )} = $$
1-11.
$$\frac{\partial}{\partial x} \tan^{a}{\left (x \right )} = $$
1-12.
$$\frac{\partial}{\partial x} \log{\left (x \right )}^{a} = $$
1-13.
$$\frac{d}{d x} f{\left (x \right )} g{\left (x \right )} = $$
1-14.
$$\frac{d}{d x} \frac{f{\left (x \right )}}{g{\left (x \right )}} = $$
常微分方程式
$2 f'(x) + 5 f(x) = 0$ を解く
# 常微分方程式
eq = sym.Eq(2 * f(x).diff(x,1) + 5 * f(x), 0)
eq
$$5 f{\left (x \right )} + 2 \frac{d}{d x} f{\left (x \right )} = 0$$
# 一般解
ans = sym.dsolve(eq)
print(ans)
ans
Eq(f(x), C1*exp(-5*x/2))
$$f{\left (x \right )} = C_{1} e^{- \frac{5 x}{2}}$$
# 特殊解
ans = sym.dsolve(eq, ics={f(0):1})
print(ans)
ans
Eq(f(x), exp(-5*x/2))
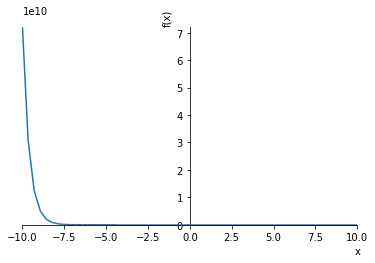
$$f{\left (x \right )} = e^{- \frac{5 x}{2}}$$
plot(ans.rhs, (x, -10, 10)) # rhs は右辺(Right-hand side)の意味
<sympy.plotting.plot.Plot at 0x7faf54dd4320>
# 特殊解で x = 2 のとき
print(ans.subs(x, 2))
ans.subs(x, 2)
Eq(f(2), exp(-5))
$$f{\left (2 \right )} = e^{-5}$$
# evalf というメソッドを使えば浮動小数点まで展開してくれる
ans.subs(x, 2).evalf()
$$f{\left (2 \right )} = 0.00673794699908547$$
課題2
常微分方程式 $f''(x) + f'(x) + 4 f(x) = 0$ について、以下の問いに答えなさい。
-
一般解を求めなさい。
-
$f(0) = 1$, $f'(0)=1$ のときの特殊解を求めなさい。
【ヒント】 ics={f(0):1, f(_).diff(x,1).subs(_,_):1} と書き _ を適切に埋めれば解けると思います。
- その特殊解に $x = 2$ を代入したときの値を求めなさい。
積分
# 積分の式
expr = x ** a
integ = sym.Integral(expr, x)
print(integ)
integ
Integral(x**a, x)
$$\int x^{a}, dx$$
# 積分の実行
integ.doit()
$$\begin{cases} \frac{x^{a + 1}}{a + 1} & \text{for}: a \neq -1 \\log{\left (x \right )} & \text{otherwise} \end{cases}$$
# このように書いても同じ
sym.integrate(expr, x)
$$\begin{cases} \frac{x^{a + 1}}{a + 1} & \text{for}: a \neq -1 \\log{\left (x \right )} & \text{otherwise} \end{cases}$$
# sym.Eq を使って等式として表記
eq = sym.Eq(sym.Integral(expr, x), sym.integrate(expr, x))
print(eq)
eq
Eq(Integral(x**a, x), Piecewise((x**(a + 1)/(a + 1), Ne(a, -1)), (log(x), True)))
$$\int x^{a}, dx = \begin{cases} \frac{x^{a + 1}}{a + 1} & \text{for}: a \neq -1 \\log{\left (x \right )} & \text{otherwise} \end{cases}$$
課題3
以下の積分の公式を、Sympy を使って完成させなさい。
3-1.
$$\int \frac{1}{x}, dx = $$
3-2.
$$\int a^{x}, dx = $$
3-3.
$$\int e^{x}, dx = $$
3-4.
$$\int \sin{\left (x \right )}, dx = $$
3-5.
$$\int \cos{\left (x \right )}, dx = $$
3-6.
$$\int \tan{\left (x \right )}, dx = $$
3-7.
$$\int \log{\left (x \right )}, dx = $$
3-8.
$$\int \frac{1}{\cos^{2}{\left (x \right )}}, dx = $$
3-9.
$$\int \frac{1}{\sin^{2}{\left (x \right )}}, dx = $$
3-10.
$$\int \left(- a + x\right)^{b}, dx = $$
3-11.
$$\int \frac{1}{\sin{\left (x \right )}}, dx = $$
定積分
expr = (x-a)*(b-x)
eq = sym.factor(sym.Eq(sym.Integral(expr, (x, a, b)), sym.integrate(expr, (x, a, b))))
print(eq)
eq
Eq(-Integral((-a + x)*(-b + x), (x, a, b)), -(a - b)**3/6)
$$- \int_{a}^{b} \left(- a + x\right) \left(- b + x\right), dx = - \frac{\left(a - b\right)^{3}}{6}$$
expr = x/(x**2 + 1)
eq = sym.Eq(sym.Integral(expr, (x, 1, 2)), sym.integrate(expr, (x, 1, 2)))
print(eq)
eq
Eq(Integral(x/(x**2 + 1), (x, 1, 2)), -log(2)/2 + log(5)/2)
$$\int_{1}^{2} \frac{x}{x^{2} + 1}, dx = - \frac{\log{\left (2 \right )}}{2} + \frac{\log{\left (5 \right )}}{2}$$
sym.integrate(expr, (x, 1, 2)).evalf()
$$0.458145365937078$$
課題4
次の定積分の式を Sympy を使って解きなさい。
$$\int_{0}^{1} \frac{4}{x^{2} + 1}, dx = $$