皆さんこんにちは。今日も引き続きChatGPT先生をお迎えして、「ChatGPTとPythonで学ぶ 強化学習」というテーマで雑談したいと思います。それではChatGPT先生、よろしくお願いします。
assistant:
もちろん、よろしくお願いいたします。まずは、全く新しい方のために「強化学習」とは何かを説明しましょう。
強化学習は機械学習の一種で、エージェントが環境と相互作用することにより学んでいきます。エージェントは、行動を通じて獲得できる報酬を最大化するように学習します。この「報酬」は実際的なもの(例えばゲームでのスコア)や抽象的なもの(例えば、推薦システムにおけるユーザー体験の向上)が考えられます。
ここで大切なのは、強化学習が「試行錯誤」による学習アプローチであるということです。エージェントは最初は何も知らない状態からスタートしますが、行動の結果としての報酬から学び、最終的には最適な行動策略(または「ポリシー」と呼ばれます)を学習します。
なお、Pythonは強化学習の実装によく使用される言語です。様々な強化学習ライブラリがPythonで利用でき、またPython自体が直感的に理解しやすい言語であるため、科学的な計算やデータ分析に非常に適しています。
user:
ありがとうございます。それでは、強化学習について、Jupyter Notebook上で学ぶためのPythonコードを書いてください。
assistant:
もちろんです、まずは強化学習の理解に必要な基本的な要素から始めましょう。この例で使用するのは非常に基本的な強化学習環境であるOpenAI GymのCartPoleタスクです。
まずは必要なパッケージをインストールします。まだインストールしていない場合は次のコマンドをJupyter Notebookのセルに入力して実行してください:
!pip install gym matplotlib numpy
次に、環境を定義して、エージェントが直面するタスクの様子を探るコードを書きます。ここでは、エージェントはランダムな行動を取るものとします。
import gym
import matplotlib.pyplot as plt
# CartPole環境を定義
env = gym.make('CartPole-v1')
# 初期状態を取得
observation = env.reset() # observationは環境の状態を表す
# ここにエピソードごとの報酬を保管
rewards = []
# エージェントが200ステップ行動する
for step in range(200):
# 環境を描画
plt.imshow(env.render(mode='rgb_array'))
# ランダムな行動を選択
action = env.action_space.sample() # actionは選択された行動
# 選択した行動を実行
observation, reward, done, info = env.step(action) # doneはエピソードが終了したかどうかを表す、infoは追加の情報を提供
# 報酬を保管
rewards.append(reward)
# もしエピソードが終了したらリセット
if done:
observation = env.reset()
# 環境を閉じる
env.close()
# 各ステップで得られた報酬のプロット
plt.plot(rewards)
plt.title('Received rewards per step')
plt.show()
このコードは、エージェントがランダムに行動するため、学習は起こりません。最終的な目標は、エージェントがポールが倒れないようにカートを制御できるように学習することです。
なお、実際に学習させるためにはQ学習やDQNなどの強化学習アルゴリズムを実装する必要がありますが、それはまた別の話となります。それらの詳細な説明や実装については、個別に深掘りすることをお勧めします。
user:
OpenAI Gymを使わずに強化学習を学べるPythonコードがあれば教えていただきたいのですが、いかがでしょうか?
assistant:
OpenAI Gymといった強化学習フレームワークはとても便利ですが、基礎から学ぶためには自分で環境を作成することが有益です。ここでは簡単な例として、Nアームドバンディッド問題を通じて強化学習を学びます。Nアームドバンディット問題では、エージェントは複数のスロットマシン(「バンディット」)から一つ選んでプレイし、選んだバンディットから得られる報酬を最大化しようとします。
Pythonでシンプルなバンディット環境を次のように実装することができます:
import numpy as np
class Bandit:
def __init__(self, n_arms):
self.n_arms = n_arms
self.bandit_arms = np.random.normal(0,1,n_arms)
def step(self, action):
return np.random.normal(self.bandit_arms[action], 1)
# 10-armed bandit
bandit = Bandit(10)
以上のコードでは、Nアームドバンディット環境をシンプルに実装しました。各バンディットアームは異なる平均報酬(bandit_arms)を持っており、エージェントのアクションはどのアームを選ぶかを意味します(step関数のaction引数)。選択したアームから得られる報酬は、そのアームの平均報酬を中心とした正規分布からサンプリングされます。
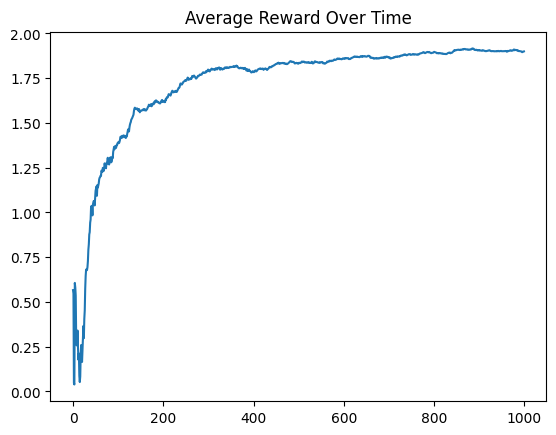
このような環境に対して適用可能なシンプルな強化学習アルゴリズムは、ε-greedyアルゴリズムです。エージェントは最も良いアームを引く(greedy)ことを試みますが、確率εでランダムに行動します。これにより新しいアームを探索(exploration)と既知の良いアームを利用(exploitation)の間のバランスを取ることができます。
n_steps = 1000
epsilon = 0.1
step_rewards = np.zeros(n_steps)
average_rewards = np.zeros(n_steps)
estimated_arms = np.zeros(bandit.n_arms)
n_pulls = np.zeros(bandit.n_arms)
for step in range(n_steps):
if np.random.rand() < epsilon:
# Randomly explore a different arm
action = np.random.choice(range(bandit.n_arms))
else:
# Greedily choose the arm which has given maximum reward
action = np.argmax(estimated_arms)
# Get the reward from the bandit for this action
reward = bandit.step(action)
step_rewards[step] = reward
n_pulls[action] += 1
# Update our estimated rewards for this arm
estimated_arms[action] += (1/n_pulls[action])*(reward-estimated_arms[action])
average_rewards[step] = np.mean(step_rewards[:step+1])
# We can plot the average reward over time, to see how our agent learned
plt.plot(average_rewards)
plt.title("Average Reward Over Time")
plt.show()
上記のコードでは、エージェントがエクスプローラブルな環境 (Bandit) を使用して、ε-greedyアルゴリズムで学習を進める様子を実装しています。行動価値の見積もりは、それぞれのアームを引いたときの平均報酬で更新します。
user:
ありがとうございます。OpenAI Gymを使わずに強化学習を学べるPythonコードとして、Nアームドバンディッド問題以外にあれば、教えていただけますか?
assistant:
もちろんです。ここでは、マルチステップの決定タスクを学ぶために、よく利用されるグリッドワールドの環境を作成しましょう。これは二次元の世界で、エージェントは目的地に到達するために最適なルートを学びます。
まずは、簡単な5x5のグリッドワールドを作り、エージェントが四方に動くことができるとします。目標地点に到達すると報酬が与えられ、そうでない時は微小なマイナス報酬(-0.04)が与えられます。これはエージェントに「早く」目的地に到達するように動機づけるためです。
まずは、この環境を作成するためのGridworldクラスを作ります。
import numpy as np
class Gridworld:
def __init__(self, grid_size=5, reward_value=1, empty_value=-0.04):
self.grid_size = grid_size
self.reward_location = (4,4)
self.agent_location = (0, 0)
self.reward_value = reward_value
self.empty_value = empty_value
self.reset()
def reset(self):
self.grid = self.empty_value*np.ones((self.grid_size, self.grid_size))
self.grid[self.reward_location] = self.reward_value
self.agent_location = (0, 0)
return self.agent_location
def step(self, action):
if action == 0: # Up
self.agent_location = (max(self.agent_location[0]-1, 0), self.agent_location[1])
elif action == 1: # Right
self.agent_location = (self.agent_location[0], min(self.agent_location[1]+1, self.grid_size-1))
elif action == 2: # Down
self.agent_location = (min(self.agent_location[0]+1, self.grid_size-1), self.agent_location[1])
elif action == 3: # Left
self.agent_location = (self.agent_location[0], max(self.agent_location[1]-1, 0))
reward = self.grid[self.agent_location]
done = self.agent_location == self.reward_location
return self.agent_location, reward, done
次にエージェントを実装します。ここでは、Q-learningという強化学習アルゴリズムを使うエージェントを作ります。ただし、以下のコードは理解を容易にするために簡略化されています。
class QLearningAgent:
def __init__(self, state_space, action_space, learning_rate=0.1, discount_factor=0.9, exploration_rate=1.0, exploration_decay_rate=0.99):
self.state_space = state_space
self.action_space = action_space
self.q_table = np.zeros(state_space + action_space)
self.learning_rate = learning_rate
self.discount_factor = discount_factor
self.exploration_rate = exploration_rate
self.exploration_decay_rate = exploration_decay_rate
def get_action(self, state):
if np.random.uniform(0, 1) < self.exploration_rate:
# Explore
return np.random.choice(self.action_space)
else:
# Exploit
return np.argmax(self.q_table[state])
def update_q(self, state, action, reward, next_state):
self.q_table[state][action] = self.q_table[state][action] + self.learning_rate * (reward + self.discount_factor * np.max(self.q_table[next_state]) - self.q_table[state][action])
def decay_exploration_rate(self):
self.exploration_rate *= self.exploration_decay_rate
# Initialize environment and agent
env = Gridworld()
agent = QLearningAgent((env.grid_size, env.grid_size), [0, 1, 2, 3])
# Run many episodes to train the agent
epochs = 500
for e in range(epochs):
state = env.reset()
done = False
while not done:
action = agent.get_action(state)
next_state, reward, done = env.step(action)
agent.update_q(state, action, reward, next_state)
state = next_state
if done:
agent.decay_exploration_rate()
print(agent.q_table)
最終的な学習結果(Q-table)をプリントすると、(0,0)から始めて(4,4)に到達するための最適な行動(移動方向)が見えてきます。このようにして、エージェントはどの方向に進むか学習し、最終的には目的地へと向かいます。したがって、この結果は、このグリッドワールド問題での強化学習の基本的な考え方を示しています。
user:
次のエラーを修正した全コードを書いてください。
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[6], line 29
27 # Initialize environment and agent
28 env = Gridworld()
---> 29 agent = QLearningAgent((env.grid_size, env.grid_size), [0, 1, 2, 3])
31 # Run many episodes to train the agent
32 epochs = 500
Cell In[6], line 6, in QLearningAgent.__init__(self, state_space, action_space, learning_rate, discount_factor, exploration_rate, exploration_decay_rate)
3 self.state_space = state_space
4 self.action_space = action_space
----> 6 self.q_table = np.zeros(state_space + action_space)
8 self.learning_rate = learning_rate
9 self.discount_factor = discount_factor
TypeError: can only concatenate tuple (not "list") to tuple
assistant:
このエラーは、タプルとリストを結合しようとして発生しています。np.zeros関数はタプル型の引数を想定しており、ここでは状態空間と行動空間の次元を示すタプルを作成する必要があります。
行動空間は通常リストとして表現されますが、ここではタプルの形で必要なため、リストをタプルに変換する必要があります。そのため、以下のように修正します。
まずは、QLearningAgentクラスの__init__メソッドを次のように修正します:
def __init__(self, state_space, action_space, learning_rate=0.1, discount_factor=0.9, exploration_rate=1.0, exploration_decay_rate=0.99):
self.state_space = state_space
self.action_space = action_space
# Here we concatenate the dimensions of the state space and the action space. We turn the action_space list into a tuple first.
self.q_table = np.zeros(state_space + tuple([len(action_space)]))
self.learning_rate = learning_rate
self.discount_factor = discount_factor
self.exploration_rate = exploration_rate
self.exploration_decay_rate = exploration_decay_rate
これで、エージェントの初期化時にエラーが発生しなくなります。全体のコードは以下のようになります:
# your code here
class QLearningAgent:
def __init__(self, state_space, action_space, learning_rate=0.1, discount_factor=0.9, exploration_rate=1.0, exploration_decay_rate=0.99):
self.state_space = state_space
self.action_space = action_space
self.q_table = np.zeros(state_space + tuple([len(action_space)]))
self.learning_rate = learning_rate
self.discount_factor = discount_factor
self.exploration_rate = exploration_rate
self.exploration_decay_rate = exploration_decay_rate
def get_action(self, state):
if np.random.uniform(0, 1) < self.exploration_rate:
return np.random.choice(self.action_space)
else:
return np.argmax(self.q_table[state])
def update_q(self, state, action, reward, next_state):
self.q_table[state][action] = self.q_table[state][action] + self.learning_rate * (reward + self.discount_factor * np.max(self.q_table[next_state]) - self.q_table[state][action])
def decay_exploration_rate(self):
self.exploration_rate *= self.exploration_decay_rate
# Initialize environment and agent
env = Gridworld()
agent = QLearningAgent((env.grid_size, env.grid_size), [0, 1, 2, 3])
# Run many episodes to train the agent
epochs = 500
for e in range(epochs):
state = env.reset()
done = False
while not done:
action = agent.get_action(state)
next_state, reward, done = env.step(action)
agent.update_q(state, action, reward, next_state)
state = next_state
if done:
agent.decay_exploration_rate()
print(agent.q_table)
user:
次のような結果が得られました。解釈してください。
[[[ 0.10988056 0.26961566 0.05452843 0.09022773]
[ 0.111531 0.3440174 0.11743943 0.04947539]
[ 0.13989809 0.22816798 0.426686 0.16167403]
[-0.01750532 -0.05215557 0.43516698 -0.03303605]
[-0.04895598 -0.04791963 0.01692693 -0.04476248]]
[[-0.06366639 0.22426744 -0.08085703 -0.10007718]
[ 0.01851937 0.41209036 0.01035783 -0.08512158]
[ 0.18720255 0.3762183 0.51854 0.2196035 ]
[-0.0227029 0.15167828 0.61473047 0.14359796]
[-0.04149725 0.02508594 0.49352931 0.04504759]]
[[-0.0773616 0.03715101 -0.0714235 -0.07653707]
[-0.0601816 0.36212956 -0.04694163 -0.06142209]
[ 0.33770648 0.6206 0.40500939 0.10287986]
[ 0.35428022 0.54275107 0.734 0.2728081 ]
[ 0.13378574 0.28800838 0.79989801 0.25621527]]
[[-0.06582173 -0.03539181 -0.05521093 -0.05413316]
[-0.06072317 0.16355911 0.00259681 -0.059862 ]
[ 0.04926128 0.29714032 0.69410485 -0.01933253]
[ 0.53009656 0.77352161 0.86 0.3836609 ]
[ 0.22097117 0.47915881 0.99484622 0.40785809]]
[[-0.06211256 -0.01427596 -0.05967864 -0.05440387]
[-0.04023867 0.43874735 0.02592969 -0.0576654 ]
[ 0.19331347 0.85683316 0.45200142 0.12926477]
[ 0.63896386 1. 0.78308833 0.6204083 ]
[ 0. 0. 0. 0. ]]]
assistant:
ここで出力されているのはQ値(state-action value)のテーブルで、Q-learningエージェントが探索と利用を繰り返しながら学習した結果です。
このグリッドワールドは5x5の大きさで、各セルはそれぞれの状態(state)を表します。また、エージェントは上、右、下、左の4つのアクションを取ることができます。したがって、Qテーブルは5x5x4の3次元配列となります。
具体的には、例えばagent.q_table[2][3]は、エージェントがセル(2, 3)にいるときに取ることのできる各アクションのQ値を表しています。このQ値が大きいほど、そのアクションを選んだときに得られる見込み報酬が高いことを示しています。
たとえば、agent.q_table[2][3][0]の値は0.35428022となっており、これはエージェントがセル(2, 3)にいて“上”に移動するアクション(アクション0)を選択したときのQ値を示しています。一方、agent.q_table[2][3][2](=0.734)は、同じセル(2, 3)にいて“下”に移動(アクション2)するときのQ値を示しており、これは“上”に移動するよりも高いQ値で、したがってエージェントにとっては望ましい行動であることを示しています。
したがって、上記のQテーブルはエージェントがどの状態でどの行動を選択すると最終的に最高の報酬を得られる可能性が高いかを学習した結果を表しています。また、Qテーブルが完成した段階であれば、エージェントはこのテーブルを元に最適な行動を決定することができます。
user:
ありがとうございます。OpenAI Gymを使わずに強化学習を学べるPythonコードとして、Nアームドバンディッド問題、グリッドワールド以外にあれば、教えていただけますか?
assistant:
はい、もちろんです。最も基本的な形の強化学習環境として、タクシーゲームを自分で実装することも可能です。ここではタクシードライバーが乗客を一定の位置で拾い、特定の目的地に運ぶという問題を解きます。
タクシー、乗客、および目的地は以下のように表示します。
タクシーは 'T'、乗客は 'P'、目的地は 'D'、そして壁(タクシーが乗り越えられない境界)は '#'で示します。
import numpy as np
class TaxiEnv:
def __init__(self, grid_size=5):
self.grid_size = grid_size
self.reset()
def reset(self):
self.taxi_row, self.taxi_col = self.grid_size - 1, 0
self.passenger_row, self.passenger_col = 0, 0
self.destination_row, self.destination_col = self.grid_size - 1, self.grid_size - 1
self.state = (self.taxi_row, self.taxi_col, self.passenger_row, self.passenger_col, self.destination_row, self.destination_col)
return self.state
def step(self, action):
if action == 0: # Up
self.taxi_row = max(self.taxi_row - 1, 0)
elif action == 1: # Right
self.taxi_col = min(self.taxi_col + 1, self.grid_size - 1)
elif action == 2: # Down
self.taxi_row = min(self.taxi_row + 1, self.grid_size - 1)
elif action == 3: # Left
self.taxi_col = max(self.taxi_col - 1, 0)
elif action == 4: # Pickup
if (self.taxi_row, self.taxi_col) == (self.passenger_row, self.passenger_col):
self.passenger_row, self.passenger_col = -1, -1
elif action == 5: # Dropoff
if (self.taxi_row, self.taxi_col) == (self.destination_row, self.destination_col):
self.destination_row, self.destination_col = -1, -1
self.state = (self.taxi_row, self.taxi_col, self.passenger_row, self.passenger_col, self.destination_row, self.destination_col)
reward = -1
if (self.passenger_row, self.passenger_col) == (self.destination_row, self.destination_col) and action == 5:
reward = 20
elif (self.taxi_row, self.taxi_col) == (self.passenger_row, self.passenger_col) and action == 4:
reward = 10
done = (self.passenger_row, self.passenger_col) == (self.destination_row, self.destination_col)
return self.state, reward, done
そして、N-アームドバンディットやグリッドワールドと同様に、この環境でQ-Learningエージェントを訓練することができます。大きな違いは、エージェントが拾い上げ(Pickup)と降ろし(Dropoff)の2つの追加的なアクションを取ることができるということです。戦略は、客をピックアップし、正しい目的地に届けるための最適なルートを見つけることです。
user:
タクシーゲームを最後まで実装してください。
assistant:
もちろんです。タクシーの環境が実装されてから、次に行うことは、Q-Learningエージェントのクラスを作成し、訓練します。タクシー環境では6つの異なるアクションが存在するため、行動空間に 6 を渡してエージェントを初期化します。
ここでは改めて QLearningAgent クラスを作成し、訓練ループを追加します。
class QLearningAgent:
def __init__(self, state_space, action_space, learning_rate=0.1, discount_factor=0.9, exploration_rate=1.0, exploration_decay_rate=0.99):
self.state_space = state_space
self.action_space = action_space
self.q_table = np.zeros(state_space + tuple([len(action_space)]))
self.learning_rate = learning_rate
self.discount_factor = discount_factor
self.exploration_rate = exploration_rate
self.exploration_decay_rate = exploration_decay_rate
def get_action(self, state):
if np.random.uniform(0, 1) < self.exploration_rate:
return np.random.choice(self.action_space)
else:
return np.argmax(self.q_table[state])
def update_q(self, state, action, reward, next_state):
self.q_table[state][action] = self.q_table[state][action] + self.learning_rate * (reward + self.discount_factor * np.max(self.q_table[next_state]) - self.q_table[state][action])
def decay_exploration_rate(self):
self.exploration_rate *= self.exploration_decay_rate
# Initialize environment and agent
env = TaxiEnv()
agent = QLearningAgent((env.grid_size, env.grid_size, 2, 2, 2, 2), list(range(6)))
# Run many episodes to train the agent
epochs = 5000
for e in range(epochs):
state = env.reset()
done = False
while not done:
action = agent.get_action(state)
next_state, reward, done = env.step(action)
agent.update_q(state, action, reward, next_state)
state = next_state
if done:
agent.decay_exploration_rate()
print(agent.q_table)
user:
次のエラーを修正した全コードを書いてください。
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
Cell In[9], line 35
33 action = agent.get_action(state)
34 next_state, reward, done = env.step(action)
---> 35 agent.update_q(state, action, reward, next_state)
36 state = next_state
37 if done:
Cell In[9], line 18, in QLearningAgent.update_q(self, state, action, reward, next_state)
17 def update_q(self, state, action, reward, next_state):
---> 18 self.q_table[state][action] = self.q_table[state][action] + self.learning_rate * (reward + self.discount_factor * np.max(self.q_table[next_state]) - self.q_table[state][action])
IndexError: index 4 is out of bounds for axis 4 with size 2
assistant:
エラーメッセージから見ると、agent.update_q の呼び出し時に IndexError が発生しているようです。 問題は具体的には、Qテーブルの走査時に次元が超えている箇所です。
この問題は、ある次元(このエラーでは4番目の次元)が、その次元の最大サイズ(このケースでは2)を超えてインデックスを作成しようとして起こります。原因は、エージェントがQテーブルを初期化する際のステートスペース指定が間違っていますが、それは TaxiEnv 環境内でのステートスペース(状態の可能な値)を正確に表現しません。
Taxi ゲームでは、タクシーはグリッド内の任意の場所に存在し、乗客はタクシーに乗っているか乗っていないかのいずれか、そして目的地もグリッド内の任意の場所に存在します。したがって、ステートスペースは以下の通りになります:
- taxi_row: 0からgrid_size-1まで
- taxi_col: 0からgrid_size-1まで
- passenger_status: 0 (タクシー内) または 1 (タクシー外)
- destination_row: 0からgrid_size-1まで
- destination_col: 0からgrid_size-1まで
したがって、Q-Learning エージェントを初期化する際のステートスペースは (grid_size, grid_size, 2, grid_size, grid_size) となります。全体のコードは以下のようになります:
class QLearningAgent:
def __init__(self, state_space, action_space, learning_rate=0.1, discount_factor=0.9, exploration_rate=1.0, exploration_decay_rate=0.99):
self.state_space = state_space
self.action_space = action_space
self.q_table = np.zeros(state_space + tuple([len(action_space)]))
self.learning_rate = learning_rate
self.discount_factor = discount_factor
self.exploration_rate = exploration_rate
self.exploration_decay_rate = exploration_decay_rate
def get_action(self, state):
if np.random.uniform(0, 1) < self.exploration_rate:
return np.random.choice(self.action_space)
else:
return np.argmax(self.q_table[state])
def update_q(self, state, action, reward, next_state):
self.q_table[state][action] = self.q_table[state][action] + self.learning_rate * (reward + self.discount_factor * np.max(self.q_table[next_state]) - self.q_table[state][action])
def decay_exploration_rate(self):
self.exploration_rate *= self.exploration_decay_rate
# Initialize environment and agent
env = TaxiEnv(grid_size=5)
agent = QLearningAgent((env.grid_size, env.grid_size, 2, env.grid_size, env.grid_size), list(range(6)))
# Run many episodes to train the agent
epochs = 5000
for e in range(epochs):
state = env.reset()
done = False
while not done:
action = agent.get_action(state)
next_state, reward, done = env.step(action)
agent.update_q(state, action, reward, next_state)
state = next_state
if done:
agent.decay_exploration_rate()
print(agent.q_table)
user:
次のエラーを修正した全コードを書いてください。
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
Cell In[10], line 35
33 action = agent.get_action(state)
34 next_state, reward, done = env.step(action)
---> 35 agent.update_q(state, action, reward, next_state)
36 state = next_state
37 if done:
Cell In[10], line 18, in QLearningAgent.update_q(self, state, action, reward, next_state)
17 def update_q(self, state, action, reward, next_state):
---> 18 self.q_table[state][action] = self.q_table[state][action] + self.learning_rate * (reward + self.discount_factor * np.max(self.q_table[next_state]) - self.q_table[state][action])
IndexError: invalid index to scalar variable.
assistant:
エラーメッセージから見ると、agent.update_qの呼び出し時にIndexErrorが発生しているようです。具体的には、スカラー変数へのインデックスが無効で、問題は次元インデックスによるアクセスがスカラーに対して実行されていることです。
これは、stateやnext_stateがタプルでなく、要素が1つだけであるために起こります。stateがタプルでないと、self.q_table[state]やself.q_table[next_state]はスカラー値を返すため、それにさらにインデックスを適用することはできません。
したがって、この問題を修正するために タクシーゲーム環境 のresetとstepメソッドを修正し、stateとnext_stateがタプルであることを確認します。
次のようになります:
class TaxiEnv:
def __init__(self, grid_size=5):
self.grid_size = grid_size
self.reset()
def reset(self):
self.taxi_row, self.taxi_col = self.grid_size - 1, 0
self.passenger_status = 1
self.destination_row, self.destination_col = self.grid_size - 1, self.grid_size - 1
self.state = (self.taxi_row, self.taxi_col, self.passenger_status, self.destination_row, self.destination_col)
return self.state
def step(self, action):
if action == 0: # Up
self.taxi_row = max(self.taxi_row - 1, 0)
elif action == 1: # Right
self.taxi_col = min(self.taxi_col + 1, self.grid_size - 1)
elif action == 2: # Down
self.taxi_row = min(self.taxi_row + 1, self.grid_size - 1)
elif action == 3: # Left
self.taxi_col = max(self.taxi_col - 1, 0)
elif action == 4: # Pickup
if self.passenger_status == 1:
self.passenger_status = 0
elif action == 5: # Dropoff
if self.passenger_status == 0 and (self.taxi_row, self.taxi_col) == (self.destination_row, self.destination_col):
self.passenger_status = 2
self.state = (self.taxi_row, self.taxi_col, self.passenger_status, self.destination_row, self.destination_col)
reward = -1
done = False
if self.passenger_status == 2: # Dropped off the passenger
reward = 20
done = True
elif action == 4 and self.passenger_status == 1: # Picked up the passenger
reward = 10
return self.state, reward, done
修正後のコードを使ってエージェントを訓練する部分は以下のようになります:
# Initialize environment and agent
env = TaxiEnv(grid_size=5)
agent = QLearningAgent((env.grid_size, env.grid_size, 3, env.grid_size, env.grid_size), list(range(6)))
# Run many episodes to train the agent
epochs = 5000
for e in range(epochs):
state = env.reset()
done = False
while not done:
action = agent.get_action(state)
next_state, reward, done = env.step(action)
agent.update_q(state, action, reward, next_state)
state = next_state
if done:
agent.decay_exploration_rate()
print(agent.q_table)
[[[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.83067624 -1.79448072 -1.9005069 -1.87052685 -1.8395234
-1.93740621]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.19 -0.1 -0.1 0. -0.1
-0.19 ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.98037956 -1.85218905 -1.77950286 -1.88000071 -1.80192965
-1.8396252 ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. -0.19 -0.1 0.
0. ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.89574372 -1.94966925 -1.76883584 -1.92187919 -1.87942765
-1.97993398]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.97893612 -1.84087173 -1.8928563 -1.96447432 -1.80604042
-1.818 ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.1 -0.19 -0.1 0. 0.
-0.1 ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.62317367 -1.47854438 -1.29142343 -2.02853627 -1.4752975
-1.62442617]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. -0.1 -0.19 0.
0. ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]]
[[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.81517489 -1.8594312 -1.82279699 -1.81018562 -1.85038795
-1.8908154 ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.19 -0.19 -0.1 -0.1 -0.21711245
-0.1 ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.7664861 -1.69802412 -1.92794517 -1.6870654 -1.75553902
-1.67464876]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.19 -0.1 0. 0. -0.45755584
-0.1 ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.91725566 -1.69140535 -1.24839892 -1.54226795 -1.86646322
-1.60729228]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. -0.19 0. 0. 0.
0. ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-2.09246086 -1.44419733 -0.96798387 -1.71709213 -1.79022627
-1.67975592]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.1 -0.1 -0.1 0. -0.22695665
-0.1 ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.54776996 -1.52719671 1.88380957 -1.60114345 -1.47436054
-1.47876773]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.1 -0.1 -0.1 0. 0.
0. ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]]
[[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.81506049 -1.87993219 -1.92109391 -1.89612618 -1.87271056
-1.8447856 ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.40951 -0.3439 -0.32337056 -0.36829 -0.54248644
-0.4755765 ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.81842531 -0.98978637 -1.6516862 -1.8641401 -1.61626989
-1.69152061]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.1 -0.1 -0.2071 -0.390241 -0.19277972
-0.19 ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.93127548 -0.57296027 3.7289415 -1.78727372 -1.4905443
-0.83808859]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.1 -0.19 -0.04719028 0. 0.
0. ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.98106431 0.57892759 6.10264533 -1.05397705 -1.20521062
-1.07398287]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.1 -0.1 -0.1 -0.1 0.
0. ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.07926515 0.91442442 11.92766771 -1.01790816 1.72483356
0.05208461]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. -0.1 0. 0. 0.59801002
0. ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]]
[[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.93394409 -1.64897619 -0.97235817 -1.9630983 -1.93910328
-1.92827097]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.73335112 0.59550534 -1.09117687 -0.83072837 -1.45959233
-0.83676039]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.97810185 6.59425609 2.23350575 -1.77344886 -1.37103406
-0.78323419]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.40951 -0.48413577 5.22170139 -0.7208464 -0.3541639
-0.30621195]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.55392132 11.33320251 4.61316247 -0.79594005 2.17974376
1.98069478]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.19 -0.19 0.87066565 -0.1 -0.16080478
-0.1 ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0.70618614 14.23778083 10.95223927 4.25535764 4.43792285
5.74333531]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.1 -0.1 0.0243153 -0.1 0.
0. ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 6.23613952 9.41638408 16.99566593 7.53199036 10.50617601
7.62985064]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. -0.1 0.
0. ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]]
[[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.97631334 8.49763201 -1.12975837 -0.21981212 -0.2065931
-1.08015534]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-1.25034689 7.7147 2.84722568 3.81247798 1.72854068
2.40697254]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 2.50954387 11.87 7.67984339 3.38463457 7.12304347
6.74653798]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0.7316551 1.21614239 5.16754649 3.26615403 9.683
5.80275516]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 4.66078415 14.3 7.74030401 8.06250733 7.9512345
8.82963564]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[-0.19 0.04915016 -0.1027293 5.44167994 2.1617261
0.18031626]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[10.54228592 17. 12.67260408 9.76387793 12.61378976
11.75764806]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 3.81492691
-0.1 ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]
[[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[13.12717297 16.33115009 15.76345699 12.49037885 15.84273752
20. ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]
[[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]
[[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]
[ 0. 0. 0. 0. 0.
0. ]]]]]]
user:
ありがとうございます。OpenAI Gymを使わずに強化学習を学べるPythonコードとして、Nアームドバンディッド問題、グリッドワールド、タクシーゲーム以外にあれば、教えていただけますか?
assistant:
はい、もちろんです。強化学習は多くの問題設定で使われており、その中にはOpenAI Gymを使わずに学べるものも沢山あります。
その中から一つ、スロットマシンの変種である「レストラン選択問題」を取り上げて説明します。この問題では、エージェントはランチに行くレストランを毎日選ばなければならず、環境はそれぞれのレストランが与える満足度(報酬)です。おいしいレストランは一貫して高い満足度を与えますが、そんなレストランを見つけるまでは、低い報酬を出すレストランを訪れることが不可避です。これは探索(新しいレストランを試す)と活用(既知のおいしいレストランに行く)のトレードオフの一例です。
import numpy as np
class RestaurantEnv:
def __init__(self, n_restaurants=10):
# Initialize parameters
self.n_restaurants = n_restaurants
self.means = np.random.rand(n_restaurants) * 5
self.stds = np.random.rand(n_restaurants) + 1
self.reset()
def reset(self):
# Reset the environment
return self.means, self.stds
def step(self, action):
# Execute action (visit a restaurant)
reward = np.random.normal(self.means[action], self.stds[action])
return reward
class UCB1Agent:
def __init__(self, n_restaurants=10):
# Initialize parameters
self.n_restaurants = n_restaurants
self.t = 0
self.means = np.zeros(n_restaurants)
self.times_visited = np.zeros(n_restaurants)
def get_action(self):
# Compute UCB1 scores for each restaurant and return the action
scores = self.means + np.sqrt(2 * np.log(self.t+1) / (self.times_visited + 1e-7))
action = np.argmax(scores)
return action
def update_policy(self, action, reward):
# Update policy
self.t += 1
self.times_visited[action] += 1
self.means[action] += (reward - self.means[action]) / self.times_visited[action]
env = RestaurantEnv()
agent = UCB1Agent()
for _ in range(1000):
action = agent.get_action()
reward = env.step(action)
agent.update_policy(action, reward)
print(agent.means)
[-0.99299456 2.04103421 1.62548658 1.79246191 4.63459803 0.10835326
-1.47380833 -0.05456808 0.50689516 2.17170574]
このコードでは、「レストラン選択問題」環境とUCB1アルゴリズムを使用するエージェントを作成し、エージェントが1000回行動を取るシナリオを実装しています。UCB1は「Exploration and Exploitation」をバランス良く行う強化学習のアルゴリズムで、エージェントはレストラン(アーム)が与える報酬(報酬)の期待値と、レストランをまだ訪れていないチャンス(探査)を考慮して行動を選びます。
user:
先ほどはε-greedyアルゴリズムを用いてNアームドバンディッド(スロットマシン)問題を解きましたが、今回のUCB1アルゴリズムを用いたレストラン選択問題と、どう違うか詳しく教えてください。
assistant:
まず、ε-greedyアルゴリズムとUCB1アルゴリズムの違いについて説明します。
ε-greedyアルゴリズムは、ランダムな探索と、以前の経験に基づく活用の間をパラメータεで調整します。 εの確率でランダムな行動を選択し、1-εの確率で最も報酬の高い行動を選択します。エージェントはランダムな探索により新しい行動を試し、活用により既知の報酬を得ます。
一方、UCB1アルゴリズムは探索と活用のバランスをアルゴリズム自体が自動的に調整します。それぞれの行動の信頼上限(UCB)を計算し、UCBが最も高い行動を選択します。UCBは行動の報酬の期待値と、行動の不確定性(既に試した回数の少ない行動ほど大きくなる)の両方を考慮します。
要するに、ε-greedyアルゴリズムは探索と活用の間のトレードオフを固定されたパラメータεで調整しますが、UCB1アルゴリズムはそれを自動的に調整します。
次に、Nアームドバンディット問題とレストラン選択問題の違いについて述べます。
実際のところ、これらの問題はゲームの詳細設定と解釈が異なるだけで、根本的な問題は同じです。それは、「ベストな選択肢を見つけるために様々な選択肢をどのように探索し、活用するか」という問題です。Nアームドバンディットでは、異なるスロットマシン、すなわち異なる「アーム」があると考えられます。それぞれのアームが異なる報酬分布を持っています。同様に、レストラン選択問題でも、各レストランは異なる「報酬」(満足度)を持つと考えられます。
したがって、探索と活用のトレードオフを最適に行うことで、どちらの問題も解くことが可能です。
user:
ありがとうございます。UCB1アルゴリズムが探索と活用の間のトレードオフを自動的に調整する仕組みについて詳しく教えてください。
assistant:
UCB1 (Upper Confidence Bound) アルゴリズムは、探索と活用のバランスを自動的に取るための強化学習アルゴリズムです。ここでの "Upper Confidence Bound"とは、行動の報酬に関する "信頼区間" の上側を指します。一般的に、信頼区間は標本統計量の不確実性を示しています。
UCB1では、報酬の期待値に加えて、「試行回数が少ないことによる」行動の不確実性も考慮に入れます。UCB1アルゴリズムでは、以下のスコアを計算し、最大スコアを持つ行動を選択します:
scores = means + sqrt((2 * log(total_counts)) / action_counts)
ここで、
-
means:各行動の報酬の平均 -
total_counts:全ての行動の試行回数の合計 -
action_counts:各行動の試行回数 -
sqrt:平方根 -
log:自然対数
平均報酬meansは活用の部分を計算します。これまで知られている結果の元で、より良い報酬をもたらす行動を優先します。
sqrt((2 * log(total_counts)) / action_counts)は探索の部分を計算します。ある行動がまだあまり試していない場合(つまりaction_countsが小さい場合)、その行動のスコアが増加します。これにより、まだ十分に試されていない行動の探索が奨励されます。
以上の二つの要素が組み合わさり、UCB1アルゴリズムでは活用と探索のバランスを上手く取ることができます。
user:
ありがとうございます。では、先ほど実装していただいた、Q-learningを用いたグリッドワールド問題と、Q-Learningを用いたタクシーゲーム問題について、違いを詳しく教えてください。
assistant:
まず、それぞれのゲームについて説明します。
-
グリッドワールド問題:これはエージェントが始点から終点まで最短で到達するルートを見つけるための問題です。エージェントはアップ、ダウン、レフト、ライトの4つの行動を選べます。それぞれの行動は特定の報酬を与え、目的地に到着すると大きなプラスの報酬が、壁に衝突するとマイナスの報酬が与えられます。
-
タクシーゲーム問題:これは乗客をピックアップ(pickup)して目的地まで運ぶ(drop off)タスクです。報酬はピックアップとドロップオフに成功した場合に与えられ、状態は(タクシーの位置、乗客の位置、目的地の位置)で表されます。エージェントは上下左右に移動、乗客をピックアップ、乗客をドロップオフの6つの行動を選べます。壁に衝突したり、乗客を摂取できない位置でピックアップしようとするとペナルティ(負の報酬)があります。
これらの問題は共に行動と報酬の組み合わせにより課題が完成する強化学習の問題ですが、以下の重要な違いがあります:
-
状態と行動の数:タクシーゲームの方がグリッドワールド問題よりも多くの可能な状態と行動があります。タクシーゲームの状態はタクシーの位置、乗客の位置、目的地の位置の3つの要素により定義され、行動は上下左右に移動するだけでなく、乗客をピックアップとドロップオフすることも選択肢として含まれています。
-
問題の複雑さ:タクシーゲームはグリッドワールド問題に比べて問題が複雑です。タクシーは乗客を見つけて運ぶという二段階のタスクを達成しなければなりません。一方、グリッドワールドは始点から終点への最短距離を見つけるだけで良いです。
-
エピソードの定義:タクシーゲームは乗客が目的地に到達するとエピソードが終了します。しかし、グリッドワールド問題ではエージェントが目標に辿り着くたびにエピソードが終了します。
どちらの問題もQ学習を使用して解くことができ、各エピソードが終わるたびにエージェントが学習して、時間を経るとともに最適な行動をさらに選択することができるようになります。
user:
グリッドワールド問題やタクシーゲーム問題は、ε-greedyアルゴリズムやUCB1アルゴリズムでは解けないのでしょうか?
assistant:
理論的には、ε-greedyアルゴリズムやUCB1アルゴリズムを用いてもグリッドワールド問題やタクシーゲーム問題を解くことは可能です。しかし、これらの問題を解くのに最適なアルゴリズムは、問題の特性によります。
ε-greedyアルゴリズムやUCB1アルゴリズムは、主に行動と直接的な報酬の関係性を学習するのに適しています。これは、マルチアームドバンディッド問題やレストラン選択問題のように、特定の行動がすぐに報酬をもたらす場合に効果的です。
これに対して、グリッドワールド問題やタクシーゲーム問題は、一連の行動を通じて目標を達成することで間接的な報酬がもたらされる問題(つまり、遅延報酬問題)であり、環境は連続的な状態を持つため、これらの問題に対してはQ-Learningのような価値ベースの方法が一般的にはより適しています。
Q-Learningはエージェントが環境から得る報酬を最大化する行動を学習しますが、その報酬は選択した行動の直後だけでなく、遠い未来にまたがって影響を与えることが考慮されます。これにより、Q-Learningは遅延報酬問題に対応することができます。
また、ε-greedy戦略やUCB1などの他の戦略は、探索と活用のバランスをとるための戦略であり、これらの戦略はQ-Learningと組み合わせてエージェントの行動選択方法をより洗練させることができます。例えば、Q-Learningの初期段階ではエージェントは環境についてあまり知らないため、ε-greedy戦略を用いてより多くのランダムな探索を行い、次第に活用の比重を増やしていくという方法があります。
user:
ε-greedyアルゴリズム、UCB1アルゴリズム、Q-Learning以外に、強化学習の戦略があれば詳しく教えてください。
assistant:
強化学習のアルゴリズムは非常に多岐にわたります。以下にいくつかの主なアルゴリズムを挙げます。
-
SARSA(同時的近似と再帰アルゴリズム): SARSAはQ-learningと非常に似たアルゴリズムであり、「状態-行動-報酬-次の状態-次の行動」(State-Action-Reward-State-Actionの頭文字を取ってSARSA)の組から学習します。Q-Learningと異なり、SARSAは行動選択策略(ポリシー)を明示的に考慮し、そのため「on-policy」の学習方法と呼ばれます。
-
Deep Q-Network (DQN): DQNは深層学習とQ-learningを結合したアルゴリズムであり、「行動価値関数」を近似するためにニューラルネットワークを使用します。これにより、非常に大きな状態空間や視覚情報を直接扱うことが可能です。
-
Policy Gradients (PG): PGアルゴリズムは価値関数の推定を必要とせずに、エージェントのポリシー(行動選択策略)を直接最適化します。これにより、連続的な行動空間を扱う問題などに適用しやすいです。
-
Actor-Critic (AC): ACアルゴリズムは価値関数(Critic)とポリシー(Actor)の両方を学習します。価値関数はどのような行動が良いかを評価し、ポリシーは実際に行動を選択します。
-
Proximal Policy Optimization (PPO): PPOはPolicy Gradientsアルゴリズムの一種で、サンプル効率と性能のバランスが非常に良いと評価されています。過去のポリシーから大きく逸脱しないように制約を加えることで、訓練の安定性を向上させます。
-
Monte Carlo Tree Search (MCTS): MCTSは木構造を利用して探索を行うアルゴリズムで、将棋や囲碁のような完全情報ゲームにおいて優れた性能を発揮します。
これらのアルゴリズムは、各々違うタイプの問題に対して強みを持っています。問題の種類や要件により、適切なアルゴリズムを選択します。また、これらの手法を組み合わせたり、改良を加えたりすることで、さまざまな強化学習問題に対する最新の解法が生まれています。
user:
深層学習と強化学習を結合した戦略は、Deep Q-Network (DQN)だけでしょうか?
assistant:
いいえ、深層学習と強化学習を結合した戦略は、Deep Q-Network (DQN)だけではありません。以下にいくつか他の主要な深層強化学習のアルゴリズムを挙げます:
-
Double DQN: DQNは選択した行動の価値を過大評価しがちである問題を改善するため、DQNの拡張版として提案されました。Double DQNでは、既存のネットワークを用いて行動を選択し、異なるネットワーク(ターゲットネットワーク)を用いてその行動の価値を評価します。
-
Dueling DQN: このアルゴリズムはアーキテクチャの変更を導入します。標準のDQNは全ての行動の価値を同時に推定しますが、Dueling DQNは状態価値と行動価値を別々に学習し、その後結合します。これにより、状態価値と行動価値の知識をより効果的に利用することができます。
-
Deep Deterministic Policy Gradients (DDPG): DDPGは連続行動空間を持つ問題を解くためのアルゴリズムです。Actor-Critic手法の一種であり、深層学習ベースの関数近似器を使用します。
-
Proximal Policy Optimization (PPO): PPOも深層学習と強化学習の組み合わせを利用しています。サンプリング効率と性能のバランスが取れたPolicy Gradient手法であり、畳み込みニューラルネットワーク等の深層学習モデルを用いてポリシーを表現します。
-
Advantage Actor Critic (A2C / A3C): A2CやA3C等はActor-Critic手法を深層学習と組み合わせ、複数エージェントが同時に学習を進めるという戦略を取っており、並列化により学習速度の向上を実現しました。
-
Soft Actor-Critic (SAC): SACはオフポリシー学習と最大エントロピー強化学習を組み合わせた手法で、深層学習ベースの関数近似器を使用します。
これらはすべて深層学習の能力を活用して、複雑な環境や大規模な状態空間、連続的な行動空間に対する強化学習の性能を向上させる戦略となっています。
user:
ありがとうございます。OpenAI Gymを使わずにSARSA(同時的近似と再帰アルゴリズム)を学べるPythonコードとして、Nアームドバンディッド問題、グリッドワールド、タクシーゲーム、レストラン選択問題以外を題材としたものを教えてください。
assistant:
SARSAを実装するための基本的なPythonのコードは以下の通りです。ここでは迷路問題(Maze problem)を題材にしています。※ただし環境の詳細(迷路の構造や初期状態など)は省略しています。
import numpy as np
class MazeSARSA:
def __init__(self, alpha=0.5, gamma=0.95, epsilon=0.1):
self.alpha = alpha # Learning rate
self.gamma = gamma # Discount factor
self.epsilon = epsilon # Exploration rate
self.q_values = {} # Initialize Q-values
def update_q_value(self, state, action, reward, next_state, next_action):
old_q_value = self.q_values[(state, action)]
next_q_value = self.q_values[(next_state, next_action)]
# Update Q-value for the current state-action pair using the SARSA update rule
new_q_value = old_q_value + self.alpha * (reward + self.gamma*next_q_value - old_q_value)
self.q_values[(state, action)] = new_q_value
def get_best_action(self, state):
# If this state was never seen before, initialize all possible actions with q-value 0
if state not in [x for x, _ in self.q_values.keys()]:
for action in range(num_actions):
self.q_values[(state, action)] = 0.0
# Choose action that have the maximum q-value for this state
actions = {action: self.q_values[(state, action)] for (x, action) in self.q_values.keys() if x == state}
best_action = max(actions, key=actions.get)
return best_action
def choose_action(self, state):
best_action = self.get_best_action(state)
# With probability epsilon explore random action, otherwise choose best action
if np.random.uniform(0, 1) < self.epsilon:
action = np.random.randint(num_actions)
else:
action = best_action
return action
# Initialize the SARSA agent and environment
agent = MazeSARSA(alpha=0.5, gamma=0.95, epsilon=0.1)
env = MazeEnvironment()
for episode in range(num_episodes):
state = env.reset()
action = agent.choose_action(state)
while True:
# Agent interacts with the environment
next_state, reward, done = env.step(action)
# Agent selects next action
next_action = agent.choose_action(next_state)
# Agent updates Q-value for the current state-action pair
agent.update_q_value(state, action, reward, next_state, next_action)
if done:
break
state = next_state
action = next_action
このMazeSARSAクラスは、SARSAアルゴリズムを用いてエージェントが迷路上での決定を下すためのものです。エージェントはその状態における最善の行動を学習し、Q値(状態-行動ペアの価値)を更新します。
ただし、ここで提供されるコード片はあくまでも一例であり、具体的な実装は問題設定(迷路の大きさ、初期状態、行動の種類、報酬等)により異なります。また、環境についての詳細な実装(MazeEnvironmentクラスなど)や必要な機能(描画機能など)は省略しています。
なお、強化学習のアルゴリズムは概念的に理解するのは他のML手法に比べて複雑であり、具体的な実装も問題設定や目的により大きく異なり得ます。したがって、より詳細な知識を得るためには教科書やオンラインの教育資源を探すことをお勧めします。
user:
迷路問題というのは、グリッドワールド問題と同じように聞こえますが、違うのでしょうか?
assistant:
迷路問題が一種のグリッドワールド問題であると言えます。グリッドワールド問題は、エージェントが離散的なセル(または"状態")で構成された世界(グリッド)を移動する問題を意味します。各セルはエージェントが存在できる場所を表し、エージェントは一方向に一歩ずつ移動できます(通常は上下左右)。
迷路問題はこのフレームワークを利用していて、エージェントの目標は特定のセル("ゴール")に到達することです。しかし、一部のセル("壁")は通過できないため、エージェントはそれらを避けてゴールに到達するように行動を学習しなければなりません。
それで、迷路問題をグリッドワールドの一種とみなすことができますが、逆に全てのグリッドワールド問題が迷路問題とは限りません。迷路問題は壁や通路があり、ゴールに辿り着く経路を見つける特殊なタイプの問題です。他のグリッドワールド問題では、エージェントが特定の状態を訪れるか、または状態間の遷移を最大化または最小化するようにするなど、条件や目的が異なる場合があります。
user:
わかりました。本質的には同じというふうに聞こえますね。それでは、Q学習とSARSAの違いについて詳しく教えてください。
assistant:
Q学習とSARSAはどちらも強化学習のアルゴリズムですが、二つの主要な違いがあります。それはどのデータを使用して学習を行うかという違いと、いつとどのように行動が選択されるかという違いです。
まず、Q学習はオフポリシーの学習アルゴリズムで、一方SARSAはオンポリシーの学習アルゴリズムです。この"ポリシー"とはエージェントが状態に基づいて行動を選択する戦略のことを指します。
-
Q学習は適応中のポリシー(行動選択の戦略)を使用してデータを生成し(探索的に行動する)、それを使用して最適なポリシーを学習します。つまり、Q学習は生成したデータを用いて、未知の行動を試みつつ最適な戦略を探ろうとします。
-
一方、SARSAは適応中のポリシーを使用してデータを生成し(探索的に行動する)、その同じポリシーを学習します。つまり、SARSAは自身が選択した行動から学習するため、「行動が選択された状況」を考慮します。これは探索と活用のバランスを保つために重要です。
また、Q学習とSARSAの更新ルールにも違いがあります。
- Q学習の更新ルール:Q(s, a) = Q(s, a) + α * [r + γ * max(Q(s', a')) - Q(s, a)]
- SARSAの更新ルール:Q(s, a) = Q(s, a) + α * [r + γ * Q(s', a') - Q(s, a)]
ここで、sは現在の状態、aはその状態で選択された行動、rは報酬、s'は次の状態、a'は次の行動、αは学習率、γは割引率をそれぞれ表します。
Q学習の更新ルールは、次のステップで可能な行動の中で最大のQ値(max(Q(s', a')))を使用します。一方で、SARSAの更新ルールでは次に実際に選択される行動(a')のQ値(Q(s', a'))を使用します。
この違いにより、SARSAは探索中のリスクを考慮に入れるために、一般的にはQ学習よりも保守的なポリシーを学びます。一方、Q学習は最適なポリシーを追求しますが、学習中に収束するまでの挙動が不安定になることがあります。
user:
ありがとうございます。強化学習と一口に言っても、色々ありすぎて難しいですね。それではお伺いしたいのですが、一見、強化学習とは関係なさそうに見えても、実は強化学習で解けてしまうような問題は、たくさんあるような気がします。「この問題は、強化学習で解けるかもしれない」と気づくためのヒントのようなものはありませんでしょうか?もしあれば教えてください。
assistant:
はい、実際に強化学習は非常に広範な問題に適用可能で、我々が日常的に遭遇する様々な課題に対しても使用できます。
強化学習を適応できる問題には以下のような特徴があります:
-
連続的なインタラクションが存在する:エージェントが何らかの環境と連続的にインタラクションする任意のシナリオは、強化学習の対象となり得ます。これはエージェントがアクションを取り、その結果に基づいて報酬を受け取りながら、時間を通じて環境に適応していく必要がある問題全般を指します。
-
遅延報酬がある:エージェントは即時の報酬だけでなく、未来に得られる報酬をも最大化できなければならないような問題に強化学習は良い適合性を示します。即ち、現在の行動が未来の報酬に影響を与える可能性がある場合、最適なポリシーを学習するために強化学習を使用できます。
-
明示的な教師が不在:強化学習は教師が明確に正解を示さない状況に適応します。つまり、正解ラベルがなく、エージェントが環境からのフィードバック(報酬)を通じて学習しなければならないシナリオを指します。
-
探査と利用のバランスが必要:エージェントが最大の報酬を得るためには、既知の最善の行動を取る(利用)と未知の行動を試す(探査)との間でバランスを取る必要があるような状況も、強化学習の適用範囲に入ります。
これらの要素が一部または全て含まれる問題は、強化学習を適用することで解決できる可能性があります。具体的な例としては、自動運転、ゲームプレイ(チェス、囲碁、ビデオゲームなど)、製造プロセスの最適化、電力の最適な供給と需要の調整、自動的にパーソナライズされた教育の提供、交通信号の制御、ポートフォリオ管理、ロボット学習などがあります。
user:
それでは最後に、強化学習をテーマにした面白ギャグを創作してください。
assistant:
もちろんです!以下のギャグをご覧ください。
合コンで男:「君の電話番号、Q学習で学んでもいい?」
女:「ええ、それって何?」
男:「まあ、何百回も何千回も試行錯誤して、最終的に君の心を勝ち取る最適な方法を見つけることだよ。」
一つの強化学習アルゴリズムがもう一つの強化学習アルゴリズムに会って言った:「君が最適な行動をしたら、私の更新が無駄になるよ。だからSARSA!」("So SARSA!"は"So sorry!"をもじった言葉遊びです。強化学習アルゴリズムのSARSAが、他のアルゴリズムの最適な行動によって自身のQ値更新が無駄になる、という意味です。)