主成分分析とは似て非なる手法として「因子分析」(Factor Analysis) があります。
主成分分析(PCA)では、説明変数に対して重み行列(固有ベクトル)a を線形結合した「主成分」 yPC1を合成しました。ここで、主成分は、説明変数と同じ数だけ定義します。
yPC1 = a1,1 x1 + a1,2 x2 + a1,3 x3 + a1,4 x4 + a1,5 + ...
因子分析では、説明変数(観測変数)x が「因子」(factor) という潜在変数から合成されるという考え方に基づき、その因子得点 f と重み行列(因子負荷) w 、そして独自因子 e を特定します(主成分分析に独自因子という考え方はありません)。
x1 = w1,1 f1 + w1,2 f2 + e1
x2 = w2,1 f1 + w2,2 f2 + e2
x3 = w3,1 f1 + w3,2 f2 + e3
x4 = w4,1 f1 + w4,2 f2 + e4
x5 = w5,1 f1 + w5,2 f2 + e5
x6 = w6,1 f1 + w6,2 f2 + e6
因子得点 f は、各個体(サンプル)が独自に持つ潜在変数です。因子得点と因子負荷の線形和(w1,1 f1 + w1,2 f2 など)を「共通因子」と呼び、観測変数独自の「独自因子」e と足し合わせることで「観測変数」として観測できるという考え方です。因子の個数は説明変数よりも小さな個数を使うのが普通で、あらかじめ決めておく必要があります。
(ただし、共通因子や因子などの用語は、調べてみた限り異なる人が異なる定義をしているように見えますので、大変紛らわしいです。私の説明のほうが間違っている可能性もありますのでその際はご容赦ください。)
因子分析を行う便利なツールとして、Pythonで利用可能なScikit-learnなどがありますが、ここでは、因子分析がどのような手法か概観するためにExcelで計算してみたいと思います。
ワインのデータ
データは UC Irvine Machine Learning Repository から取得したものを少し改変しました。
https://github.com/maskot1977/ipython_notebook/blob/master/toydata/wine.xlsx
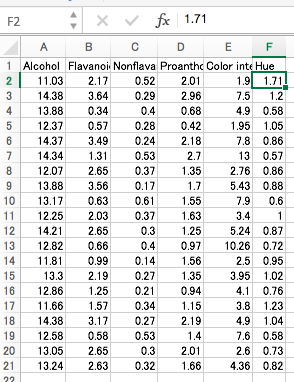
今回のデータは、20個のワインの銘柄の特徴が、6種類の「観測変数」(x1, x2, x3, x4, x5, x6) で表されています。この6変数を説明変数とします。
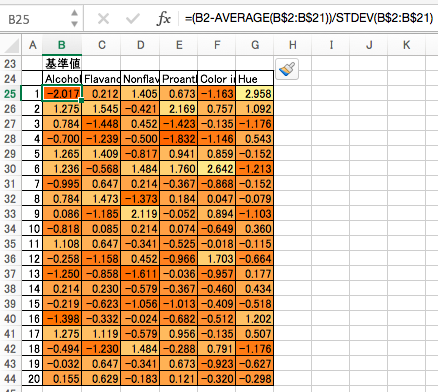
基準値
各列に対して、平均値を引いたものを標準偏差で割ります。
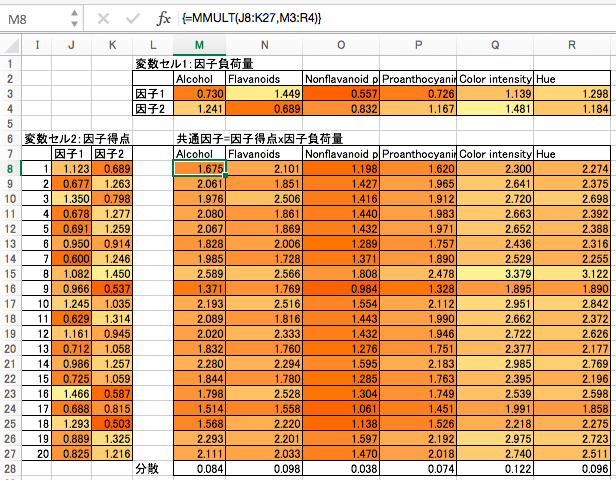
因子負荷量、因子得点、共通因子
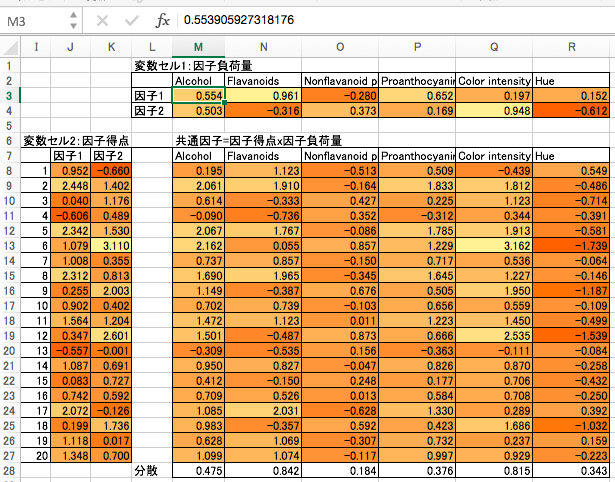
因子負荷量 w は観測変数ごとに与えられる係数、因子得点は個体(サンプル)ごとに与えらえる係数で、それらの線形和が「共通因子」になります。因子分析の目的は、この因子負荷量と因子得点を求めることです。ここではまず、因子負荷量と因子得点を乱数で初期化しておき、その積を仮の共通因子とします。現時点ではランダムな数字で算出されたデタラメな数値が入ってます。
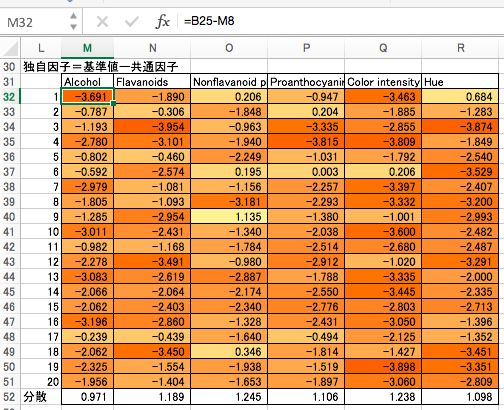
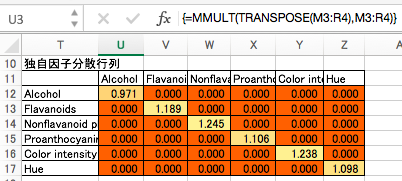
独自因子
実際の観測値と共通因子との差を、共通因子では説明できない「独自因子」とします。現時点ではランダムな数字で算出されたデタラメな数値が入ってます。
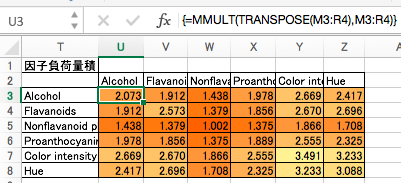
因子分析が推定する相関行列
まずは因子負荷量の自分自身に対する行列積を計算し、それを「もしも独自因子がまったくなく、共通因子だけで観測事象が説明できると仮定したときの相関行列」と考えます。現時点ではランダムな数字で算出されたデタラメな数値が入ってます。
次に、独自因子による影響として、対角成分に独自因子の分散を、それ以外の成分に0を入れた行列を作成します。現時点ではランダムな数字で算出されたデタラメな数値が入ってます。
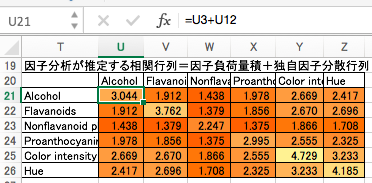
上記2つの行列の和を、「因子分析が推定する、共通因子と独自因子の和による相関行列」とします。現時点ではランダムな数字で算出されたデタラメな数値が入ってます。
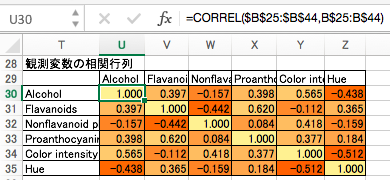
観測変数の相関行列
実際の観測変数の相関行列を作成します。
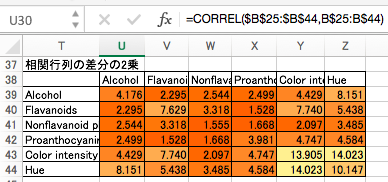
2つの相関行列の差分を最小化する
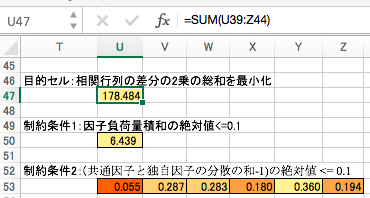
「因子分析が推定する、共通因子と独自因子の和による相関行列」と、「実際の観測変数の相関行列」の差分の2乗和を計算します。これを最小化する因子負荷量と因子得点を計算するのが、因子分析の目的になります。
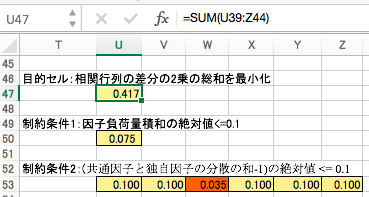
目的変数と制約条件を整理します。目的変数は、2つの相関係数の差分の2乗和で、これの最小化が目的です。
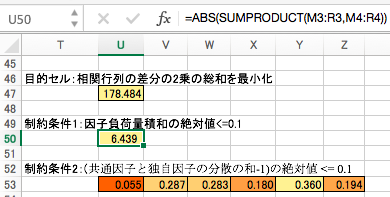
制約条件その1としては、因子負荷量の積和をゼロにするというのがあります。ぴったりゼロにするのは難しいので、ここでは絶対値を 0.1 以下にすることにします。
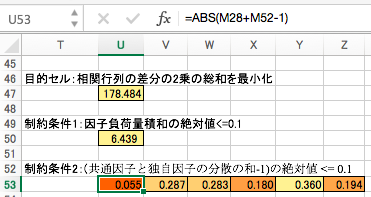
制約条件その2として、各々の観測変数に対して、共通因子の分散と独自因子の分散の和を1にするというのがあります。ぴったり1にするのは難しいので、ここではその和から1を引いた数の絶対値を 0.1 以下にすることにします。
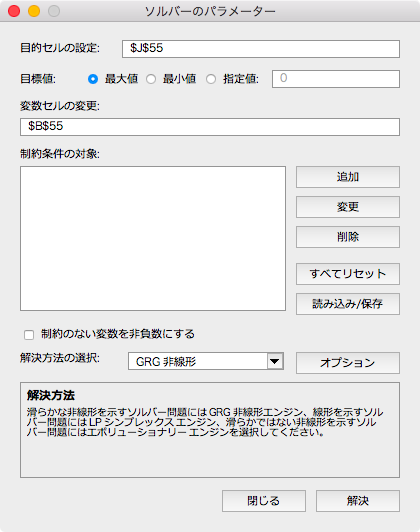
ソルバーを立ち上げ、以上の条件を間違えずに入力します。
「解決」を押すと、けっこう時間がかかりますが、答えが返ってきます。収束しない場合は、ランダムな初期値を変更して計算し直してください。
収束後の目的変数と制約条件の数の例はこちらになります。
最適化後の因子負荷量と因子得点
収束後(最適化後)の因子負荷量と因子得点の例はこちらになります。乱数による初期化を行なっているので、答えが必ずしも同じになるとは限りません。
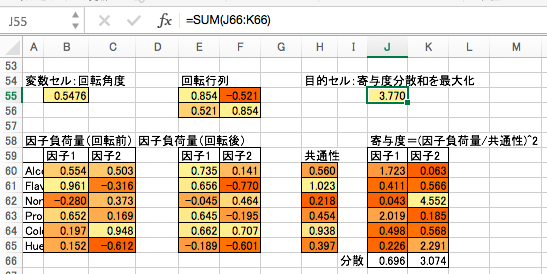
バリマックス回転
因子分析の肝の部分は以上で終了ですが、その後に直交回転を行うことがあります。以下に述べるバリマックス回転はそのひとつで、因子の解釈を容易にする目的で、全因子によって説明できる分散を最大にするように回転します。
これをソルバーで実行するには、以下のようにします。
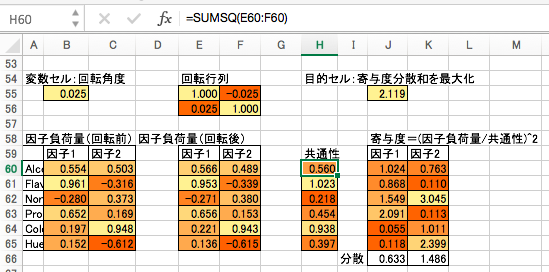
- まず回転角を乱数で初期化し、回転行列を作成します。
- 回転行列との行列積により、回転前の因子負荷量から回転後の因子負荷量を算出します。
- 「共通性」を算出します。ここでいう共通性とは、因子負荷量の2乗和です。
- 因子負荷量を共通性で割って2乗したものを「寄与度」と言います。その分散を求めます。
※ 「観測値の2乗に対する、因子負荷量の2乗和の割合」のことを「共通性」と呼んでいる文献もあります。また、「共通因子」のことを「共通性」と呼んでいる文献もあります。非常に紛らわしい(単に私が誤解しているだけかもしれませんが)。
- 寄与度の分散の和が最大になるような回転角をソルバーで求めます。
最適化後の値の例はこちらになります。
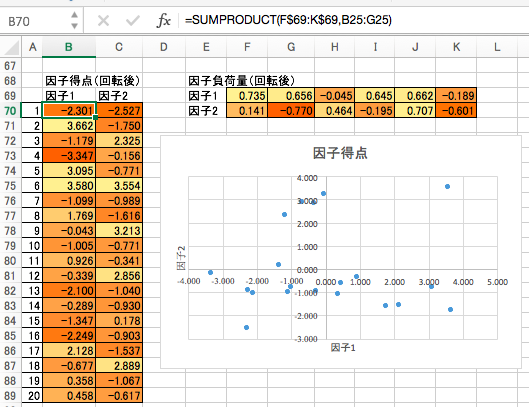
回転後の因子得点と因子負荷量
因子得点を用いて、各個体(各サンプル、ここではワインの銘柄)をプロットできます。そのプロットの横軸・縦軸がいかほどの意味を持つかは、次の因子負荷量を用いた観測変数のプロットによります。
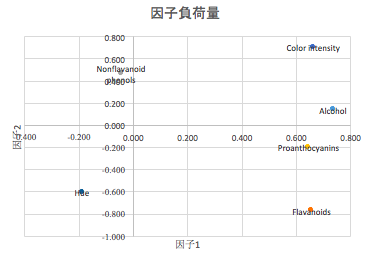
因子負荷量を用いて、各観測変数をプロットできます。因子1は何を意味しそうか、因子2は何を意味しそうか、解釈してみましょう。
課題
-
ここでいう「共通性」は、回転前と回転後でどのように変わるか説明してください。
-
主成分分析による結果と比較してください。
-
実習用データ から「都道府県別アルコール類の消費量」を取得し、同様に因子分析を行い、その結果について考察してください。また同様に、主成分分析による結果と比較してください。